Σ-Δ A/D在电机控制系统中的应用研究

温金鑫，王轲，贺永鹏，徐莉，张凯

（1.天津电气科学研究院有限公司，天津300180；2.中国石油化工集团天津分公司，天津300271）

高精度的A/D 转换器从使用技术的角度可分成两大类：一类采用并行比较和双斜积分等技术，主要依靠复杂的电路设计和器件的高精度得到高精度的A/D输出，使用高性能的前端抗混叠滤波器在一定程度上防止了混叠噪声的影响，但也增加了设计的复杂程度；另一类是Σ-ΔA/D 转换，采用过采样技术、量化噪声整形技术以及Σ-Δ调制技术，大大改善了基带内的信噪比，在提高分辨率的同时对前置抗混叠滤波器的性能要求也明显降低，通过增加A/D转换器中的数字电路比例，降低模拟电路比例，降低对模拟电路的精度要求，不仅能够实现高精度的A/D转换而且成本较低，适合有成本要求的低频场合［1］。因此，近年来Σ-Δ A/D转换器得到了越来越多的应用。

电机数字控制系统对检测信号的精度及实时性有较高的要求。使用平均值滤波的Σ-ΔA/D转换器实时性好，但输出精度较低，常常不能满足精度要求。本文针对电机控制系统低延时、高精度的要求，设计了一种基于FPGA 的Σ-ΔA/D方案，采用ADS1204进行二阶Σ-Δ调制，FPGA实现CIC（级联积分梳状）滤波，既减少滤波环节的延迟，又能达到较高的转换精度，同时CIC 算法简洁，采用级联积分和微分器，不使用乘法器，FPGA资源占用很少。

本设计分调制和滤波两部分。调制部分采用TI 公司的ADS1204 芯片，滤波部分是设计重点，首先在模型中对调制信号分别进行CIC滤波和平均值滤波，分析CIC 滤波对比平均值滤波的优势，然后通过仿真评估CIC 滤波方案，分析阶数、抽取率对实时性、精度的影响，并提供了滤波器参数选择依据。最后，对本设计进行实验验证。

1 Σ-Δ调制器

1.1 Σ-Δ调制原理

Σ-Δ调制模块是采用过采样的方法将模拟电压转换成1 位数字量的转换器，是整个Σ-ΔA/D的核心。一阶Σ-Δ调制模块由差分放大器、积分器、比较器与1位的DAC 组成，其工作原理见图1a，输入信号减去来自1 位DAC 的信号，结果作为积分器的输入，积分器的输出作为比较器也就是1 位A/D 的输入，比较器的输出是代表输入信号的1 位数字位流，1 位DAC 将此输出位流转换为模拟波形，回馈给差分为放大器。当系统达到稳定工作状态时，积分器的输出信号是全部误差电压之和，同时积分器可以看作是低通滤波器，拥有抑制噪声的能力［2］。

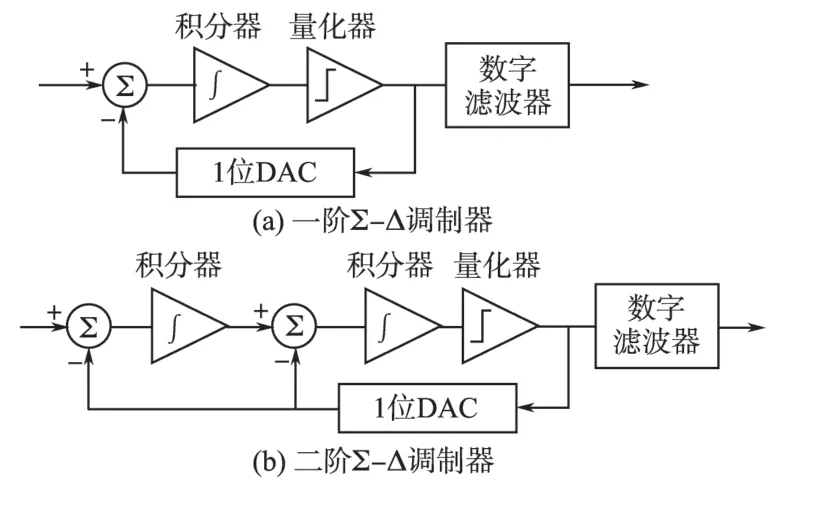
图1 Σ-Δ调制器模块图Fig.1 Σ-Δ modulator block diagram

将一阶Σ-Δ调制器进行级联就可以得到二阶的Σ-Δ调制器，见图1b。与一阶Σ-Δ调制器相比，二阶的调制器具有更好的噪声成形特性，可以把量化噪声进一步推到有用带宽之外。

1.2 ADS1204 Σ-Δ调制应用

本文采用TI 公司的ADS1204Σ-Δ调制器。ADS1204是一款高性能二阶Σ-Δ调制器，具有16位分辨率，4 个独立通道，性能高，采用5 V 电源供电。其输入采用差分型式，温度范围-40～105°C，适于工业控制领域。结合适当的滤波器及调制速率，ADS1204能实现高精度A/D转换。

模拟信号通过ADS1204Σ-Δ调制后输出1位高速比特流，ADS1204芯片的输入输出特性参见图2，图2中u表示输入模拟量，v表示输出调制信号。在某段时间内输出比特流的平均值代表输入信号在这段时间的平均值，即比特流中“1”的密度对应着模拟输入的大小。

本文的电机控制采集电路输入信号调理电路参见图3。采用典型的单端转差分电路连接ADS1204 的输入，通过ADS1204 进行二阶Σ-Δ调制，将输出的一位比特流传给FPGA 进行滤波。

图3 输入信号调理电路Fig.3 Input signal processing circuit

2 CIC滤波器

2.1 CIC数字抽取滤波器原理

数字抽取滤波器作为Σ-ΔA/D的重要组成部分，主要作用是降低系统的采样频率，使系统工作在奈奎斯特频率，滤除基带外的噪声，提高信噪比，起到抗混叠的作用。

在Σ-ΔA/D 转换器中，为了能有效将Σ-Δ调制器输出的高采样率、低分辨率的比特流信号转换成以奈奎斯特采样频率输出的高分辨率数字信号，常使用级联积分梳状（CIC）滤波器进行抽取。K阶CIC滤波器最大的特点是在实现过程中不需要使用乘法器，通过在高采样速率下（采样率fs）级联K 阶积分器，随后在低采样速率下（采样率fs/M）级联K 阶微分器来实现。该架构采用环状运算，结构上是稳定的［3］。CIC 滤波器的结构如图4所示。

K阶滤波器的传递函数如式（1），式中M表示抽取率，K为滤波器阶数。

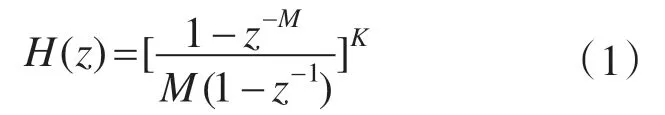
相应的频率响应为

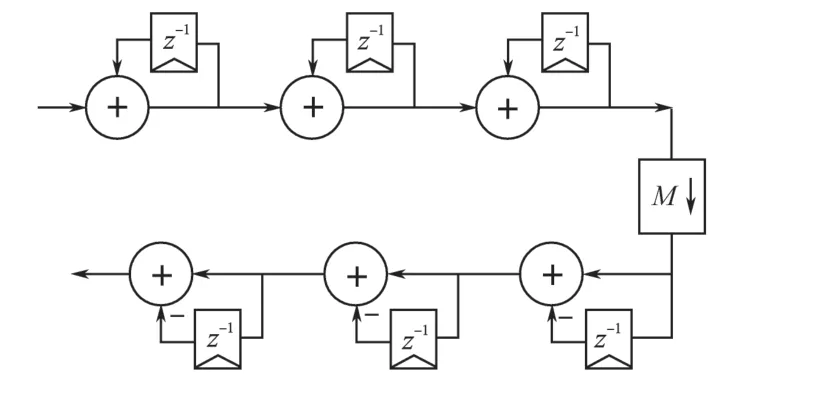
图4 3阶CIC抽取滤波器结构框图Fig.4 3rd-order CIC decimation filter structure diagram

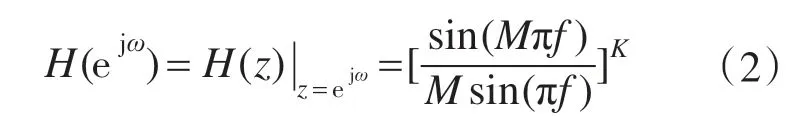
图5为K=1和K=3时CIC抽取滤波的频率响应，可以看出K增大后，通带边缘变得陡峭，滤波效果变好，高频抑制效果得到明显改善。

图5 不同阶数CIC滤波器频率响应图Fig.5 Frequency response chart of CIC filter with different order

2.2 仿真分析

本文采用非理想条件下二阶Σ-Δ调制的仿真模型，见图6。它可模拟实际硬件电路中各个环节对Σ-Δ调制引入的噪声，如时钟抖动、kT/C 噪声、运算放大器的噪声、有限增益、带宽、翻转率及电压限幅等。由于考虑了各种非理想因素对调制过程的影响，采用此模型进行仿真比较接近实际的调制过程。

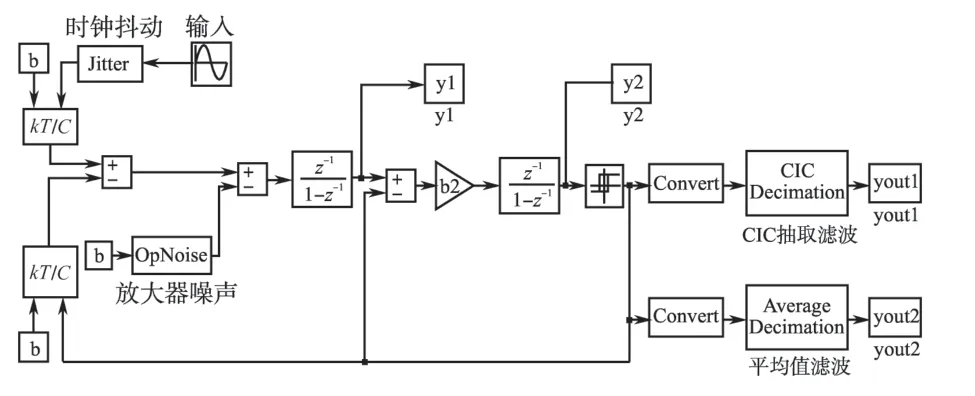
图6 Σ-ΔA/D 仿真模型Fig.6 Σ-ΔA/D simulation model

采用f=50 Hz的模拟工频正弦信号作为仿真输入信号，调制器采样频率为10 MHz。对输入信号进行过采样，并通过模型对信号进行二阶Σ-Δ调制，然后对调制结果分别进行CIC 滤波和平均值滤波。首先通过修改CIC滤波器的阶数、抽取率、延迟等参数，对CIC 滤波器进行全面仿真，研究滤波器各参数对转换效果的影响。其次使用平均值滤波进行对比仿真，研究CIC滤波器对比平均值滤波的优势。

从CIC 滤波器的原理分析可知，随着阶数的增大，通带边缘变得陡峭，对高频噪声的抑制更好。为了进一步研究阶数对滤波效果的实际影响，固定抽取率为128，取不同阶数（K=1，2，3）CIC 滤波器进行仿真，对结果在频域进行分析并计算相应的信噪比与有效位数，得到图7。从图7中可见随着阶数K的增大，信噪比和有效位数逐步改善。当K<3时，信噪比和有效位数达不到精度要求；当K=3时，信噪比和有效位数明显改善，可以达14位精度。依此趋势，继续增大阶数K可以持续改善精度，但改善幅度逐渐减小，同时增加了运算模块，导致更长的延时及更多的硬件消耗。综合考虑，选择三阶CIC滤波器。

图7 不同阶数CIC滤波器的频率谱密度图Fig.7 Frequency spectral density chart of CIC filter with different order

为了研究不同抽取率对延迟时间及精度的影响，选取不同抽取率的三阶CIC对调制信号进行抽取滤波，并计算其信噪比及有效位数。设定调制器的采样频率为10 MHz，抽取率M 取不同值，仿真结果见表1。可见随着抽取率的增大，信噪比及有效位数不断增大，这是由于随着抽取率的增大，CIC滤波器对高频噪声的滤波更加彻底。

表1 不同抽取率的CIC滤波仿真结果Tab.1 Simulation results of CIC filter with different decimation ratio

同时可以看到，随着所选择抽取率的增大，滤波的延迟时间也随之增大。CIC算法的特点是以牺牲实时性来提高精度，因此在选取CIC滤波器时，并不是精度越高越好，而是要折衷考虑转换精度与实时性。

在图6模型中对平均值滤波与CIC滤波进行对比，分别对两种滤波结果进行SNR计算及频域分析，结果见图8。从图8a的曲线看出，三阶CIC滤波的信噪比值整体高于平均值滤波。相同抽取率时，CIC 滤波器的有效位数高于平均值滤波器，说明三阶CIC 滤波实现的A/D 转换精度高于平均值滤波。

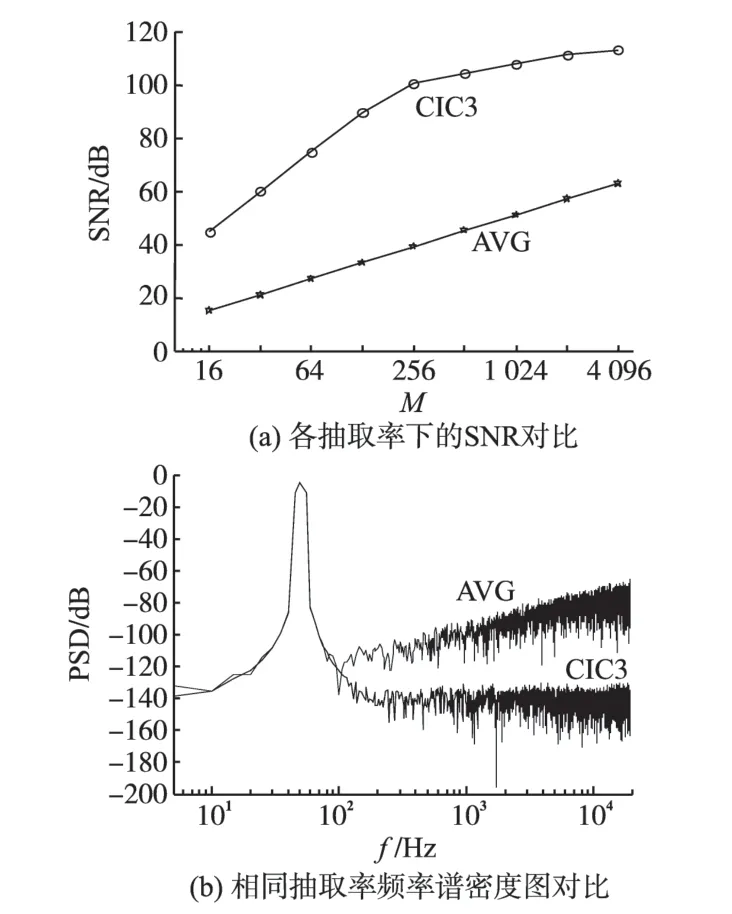
图8 三阶CIC滤波与平均值滤波对比Fig.8 Comparison between 3rd-order CIC filter and mean filter

从图8b可知，在基频段两种滤波方法曲线几乎重合，频谱特性相似。而在高频段，三阶CIC滤波的频谱幅值明显低于平均值滤波，说明三阶CIC 滤波对高频噪声的过滤效果好于平均值滤波，这与图8a中三阶CIC滤波的信噪比高于平均值滤波的结论相符。

3 实验验证

本设计的验证实验系统如图9所示。信号发生器模拟交流电机控制系统信号进入采集电路，信号调理后，ADS1204 对模拟量进行Σ-Δ调制，调制后的比特流传给FPGA 进行滤波，通过串口通讯将结果传回PC 机进行分析。采集电路及FPGA芯片都集成在自制的控制板卡上，FPGA选用Altera公司的CycloneⅣ系列芯片。

图9 验证实验系统Fig.9 Verification experiment system

本文CIC 滤波器使用VHDL 语言编程，下面以抽取率等于32为例说明三阶CIC滤波器在FPGA 中的实现方法。参见图10，MCLK 与MDAT分别为来自调制芯片的时钟与调制比特流，M为抽取率，输出Q为A/D转换结果，QV为输出有效信号。

图10 三阶CIC滤波器的FPGA程序实现Fig.10 3rd-order CIC filter implementation in FPGA

首先以MCLK 为时钟进行3 级积分运算，积分器由1 个16 位的 加法器与1 个16 位的D 触发器组成。第1 级积分器实际上是1 个累加器，负责累计MDAT为1时MCLK 的脉冲数，即实现以MCLK 为节拍对MDAT 中的‘1’值进行累加；第2，3 级积分器的D 触发器一直处于使能状态，MCLK时钟触发时，将上一级的运算结果累加到当前值上，完成第2，3级积分运算。

积分运算后以MCLK/M 为时钟进行3 次微分运算，微分器由1 个16 位的D 触发器和1 个16位的减法器组成，MCLK/M 时钟触发时，将前一级结果减去上一周期的对应值即完成1次微分运算，如此重复3次完成三阶微分运算。

总线的宽度应随抽取率变化，当M=32 时取16位总线宽度，在调制比特流恒为‘1’时，Q输出16h’7FFF，对应最大模拟量；在比特流恒为‘0’时，Q输出16h’0000，对应最小模拟量。

抽取率取不同值时CIC3 模块的资源占用情况参见表2。从表2可看出，随着CIC滤波器阶数的升高，占用资源增加。因此在选择滤波器参数时，不仅要考虑实时性，转换精度，还要适当考虑资源占用情况。

表2 资源占用随不同抽取率的变化Tab.2 Resource consumption varies with different decimation ratio

在验证实验中，信号发生器模拟交流电机控制系统50 Hz 交流信号，经调制滤波后转换数据传回PC 机进行频域分析，计算实际A/D 的信噪比及有效精度。使用不同的抽取率进行试验，结果见表3。这里实验数据与仿真数据趋势相同但略有差别，主要原因是实际硬件电路中引入的噪声与仿真模型中的模拟噪声不尽相同。

总之，CIC滤波器在抽取率高的情况下，采集精度高，在抽取率低的情况下，响应速度快。在不改变硬件配置情况下，仅通过改变FPGA 程序的可配置抽取率参数，就可满足不同的精度和实时性需求，使本设计适用于不同的应用场合。

本设计应用在交流电机控制系统中，计算部分要求精度高，选取抽取率为128的滤波器，保护部分要求响应速度快，选取抽取率为32 的滤波器，可分别满足不同的精度和实时性需求。

4 结论

本文设计的Σ-ΔA/D 数据采集系统采用ADS1204 实现二阶Σ-Δ调制，FPGA 实现对调制信号的CIC滤波。通过对滤波器的综合分析，考虑转换精度、资源占用、延时等指标，确定了滤波器的各参数选择。本设计方案已经用于交流电机控制系统中，能够满足电机控制系统对A/D转换的精度及实时性要求，占用硬件资源相对较少，可靠性高。

［1］ 袁小龙.高性能Σ-Δ调制器、模数转换器的研究［D］.杭州：浙江大学，2009.

［2］ 赵宏亮.基于Sigma-Delta 转换器的数字滤波器设计［D］.天津：天津大学，2007.

［3］ Oljaca M，Hendrick T.Combining the ADS1202 with an FPGA Digital Filter for Current Measurement in Motor Control Applications［C］//Application Report.Literature Number SBAA094，2003.