基于电流迭代优化的SRM总转矩TSF闭环控制
党选举,肖逢,林诚才
(桂林电子科技大学电子工程与自动化学院,广西桂林541004)
开关磁阻电机具有结构坚固、无需稀土材料、机电能量转换效率高、可高速运行、可频繁启停、调速范围宽等优点,非常适合应用于混合电动汽车和纯电动汽车的动力牵引场合。但是,电机定转子的双凸极结构与高度磁饱和的运行状态决定了SRM存在转矩脉动大的固有缺陷,尤其是在低速运行时,电机的转矩波动强烈,将会引起系统的震动,制约了它在电动汽车领域的推广和应用。因此,开关磁阻电机转矩脉动抑制的研究意义重大。
为了减少转矩脉动,国内外学者在SRM控制领域展开研究,并已经取得了大量颇具影响力的研究成果[1-3],文献[4]将异步电机的直接转矩控制(direct torque control,DTC)思想引入到SRM,提出了基于SRM的直接转矩控制策略;其他主要研究成果有直接瞬时转矩控制(direct instantaneous torque control,DITC)策略[5]、转矩分配函数(TSF)控制策略[6]等。
本文在传统TSF开环控制基础上,提出了基于电流迭代学习的SRM 总转矩TSF 闭环控制策略。该策略将电机总转矩信息反馈到转矩控制器,构成转矩闭环控制系统,以迭代学习方式,使参考电流不断逼近最佳电流曲线,最终达到减小转矩脉动的目的。并根据理想参考电流曲线的特点,设计了分区细化的电流滞环控制器,改进的电流滞环控制器有效提高了电流的控制性能,可进一步减小电机的转矩脉动。
1 迭代学习控制算法
SRM 的各相转矩是根据转子位置角信息进行重复控制输出,电机输出的电磁转矩具有周期脉动的特点,而迭代学习控制是利用系统先前的控制经验和输出偏差来修正当前的控制量,十分适用于重复控制场合,且控制过程不需要对象模型。因此迭代学习控制算法十分适用于SRM 的转矩脉动抑制控制。
开环P 型迭代学习控制的一般结构如图1所示。
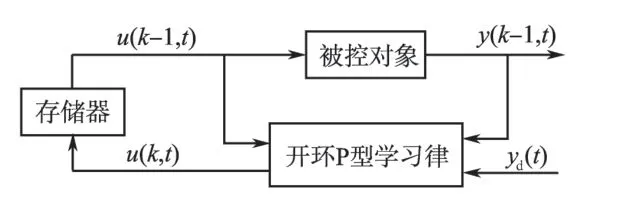
图1 迭代学习控制原理图Fig.1 Principle diagram of ILC
开环P型迭代学习算法的数学表达式[7]为
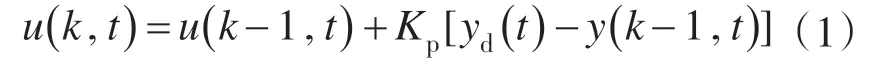
式中:Kp为开环迭代学习系数;k为当前迭代周期次数;t为当前迭代时间点;yd(t )为t时刻的给定值,各迭代周期yd(t )保持不变;y( k- 1,t )为第k-1次迭代t 时刻的响应值;u( k- 1,t )为第k-1次迭代t 时 刻 的 控 制 量;u( k,t )为 第k 次 迭 代t 时 刻的控制量。
2 转矩控制器的设计
图2 为SRM 传统TSF 转矩开环控制系统框图,控制器部分由转矩分配器、转矩—电流转换器及电流控制器3 部分组成,通过转矩分配器将参考转矩Td分配成开通相参考转矩Tup和关断相参考转矩Tdn,再经过转矩—电流转换器计算得到各相参考电流,各相参考电流分别使用电流闭环控制器跟踪控制。

图2 SRM传统TSF转矩开环控制系统框图Fig.2 Block diagram of TSF open-loop control for SRM
由于SRM的电磁关系十分复杂,实际中难以得到准确的转矩—电流转换模型,通常会使用简化的线性电感模型来实现转矩—电流的转换[8],但是简化模型不能准确描述电机相绕组电感的非线性特性,导致参考电流与理想电流存在偏差。为了解决这个问题,本文在传统TSF转矩开环控制基础上,提出了如图3 所示的基于电流迭代学习的SRM 总转矩TSF 闭环控制策略。该策略以转矩脉动最小化为目标,将给定转矩Td与总转矩Te的偏差eT输入补偿器,根据转子位置角信息,进行迭代学习控制,分配输出参考电流补偿量和,补偿量再分别叠加到参考电流和,得到理想的参考电流和。

图3 基于ILC的SRM总转矩TSF闭环控制系统框图Fig.3 Block diagram of closed-loop control of total torque TSF for SRM based on ILC
2.1 转矩分配函数的选择
在转矩分配控制研究中,常用的转矩分配函数有转矩线性分配函数、转矩正弦分配函数、转矩指数分配函数及转矩立方分配函数[9]等,从控制效果和运算量方面考虑,本文选择立方分配函数作为转矩分配函数。
图4 为转矩立方分配曲线,其中立方分配函数的表达式为
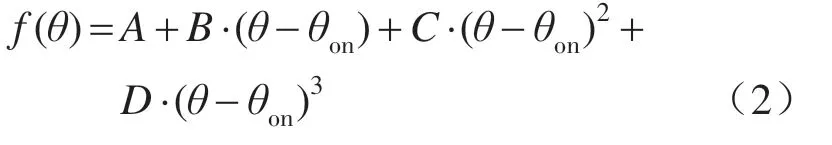
式中:θ为转子位置角;θon为开通角;A,B,C,D均为常数。
在函数上升区间,函数必须满足下式的2个条件:
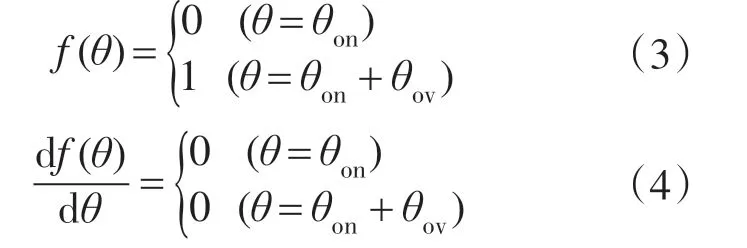
式中:θov为换相重叠角。
令式(2)中的A = 0和B = 0,由式(3)和式(4)可推导出
将A,B,C,D的值代入式(2)得到具体的转矩分配函数为
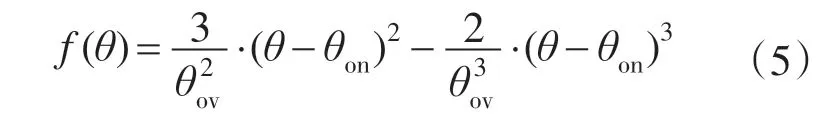
设给定总转矩为Td,则C—A换相重叠区开通相和关断相的参考转矩分别为
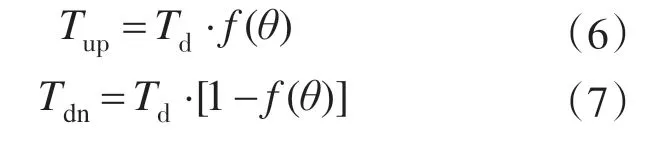
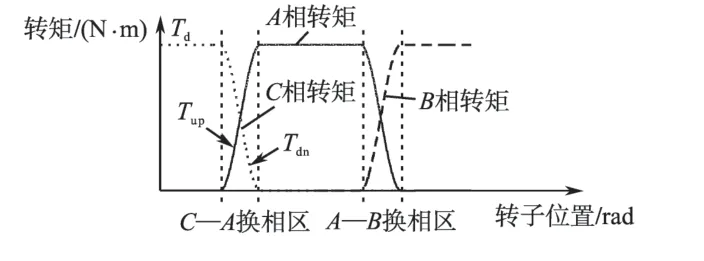
图4 转矩立方分配曲线Fig.4 Curves of torque cubic sharing
2.2 转矩—电流转换器的简化模型
线性电感变化曲线如图5 所示,当不考虑磁饱和与边缘效应时,SRM的相电感L相对转子位置θ呈梯形曲线变化,其电磁转矩数学模型可简化为[8]

式中:i为相电流值;L为相电感值;θ为电机转子位置角。
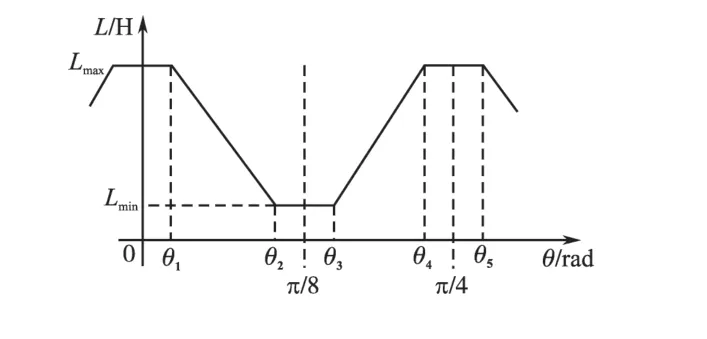
图5 线性电感变化曲线Fig.5 Curve of linear inductance
由式(3)可得,转矩—电流转换公式为

若令KL=∂L/∂θ,KL为相电感的变化率,对于呈梯形曲线变化的线性电感模型,KL为常数,则利用转矩—电流转换公式,由TSF设计的各相参考转矩可计算得到相应参考电流。
2.3 迭代学习电流补偿器的设计
为了补偿因简化的线性电感模型导致的参考电流偏差,设计了如图6 所示的基于迭代学习的电流补偿器。补偿器引入电机总转矩负反馈,将给定转矩Td与总转矩Te的偏差信息作为迭代学习控制器的输入,根据转子位置角信息θ,采用开环P 型迭代学习算法,对参考电流进行迭代补偿控制,使其不断逼近理想的电流曲线。
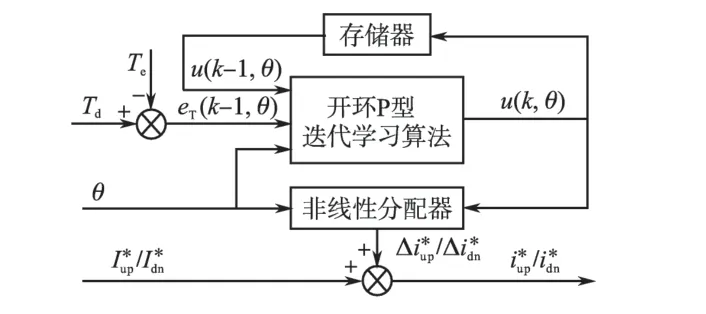
图6 迭代学习电流补偿器的结构Fig.6 Structure of the iterative learning current compensator
参考电流优化曲线如图7 所示,在单相导通区和换相重叠区,有不同的激励相数,其参考电流的补偿需要分别处理。在单相导通区,只需要控制单相绕组电流,总电流补偿值u 可直接叠加到由转矩计算的单相参考电流,得到补偿后的参考电流。
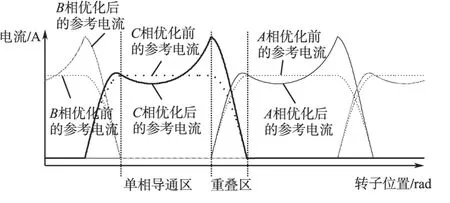
图7 参考电流优化曲线Fig.7 Optimization curves of the reference current
在换相重叠区,开通相和关断相绕组需要同时激励,且开通相电流上升,关断相电流下降,为了实现重叠区和单相导通区参考电流曲线的平滑过渡,开通相和关断相参考电流的补偿通过图6中的非线性分配器,根据转子位置角信息,由总电流补偿值u 用式(5)的立方分配函数f(θ)分配计算得到开通相和关断相的参考电流补偿值和,并分别叠加到由开通相和关断相转矩计算的参考电流和,得到补偿后的参考电流和经过反复迭代补偿控制,最终得到图7 中优化后的各相参考电流曲线。
在控制过程中,转矩偏差是按设定的时间间隔采样获得,但基于转子位置角的迭代学习算法要根据转子位置角间隔进行运算,各采样时刻的转矩偏差数据不能直接用于迭代运算。迭代运算线性插补原理图如图8 所示,借鉴文献[10]中设计的线性插补方法,利用两个相邻采样点的转矩偏差数据值,以线性插补的方式,计算各迭代位置点的转矩偏差数据值,有效地解决了迭代位置的数据无法直接采样获得的问题。
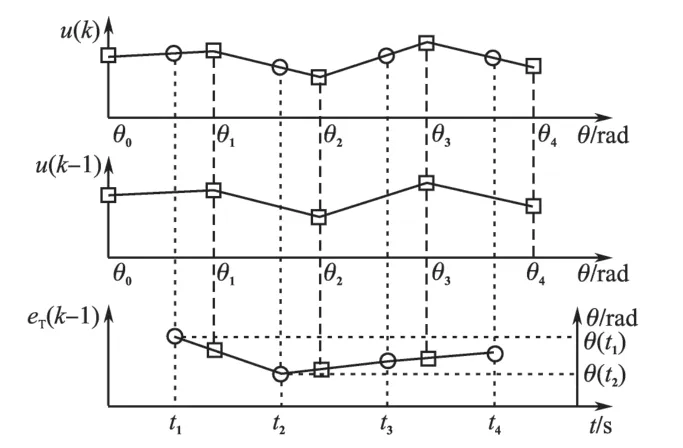
图8 迭代运算线性插补原理图Fig.8 Schematic diagram of linear interpolation of iterative learning algorithm
如图8 所示,其中□为迭代运算位置点的数据,○为采样时间点的输入输出数据。利用t1和t2采样时刻的转子位置角信息和转矩偏差数据值,采用式(10)的线性插补公式,可计算得到迭代位置点θ1的转矩偏差数据值:
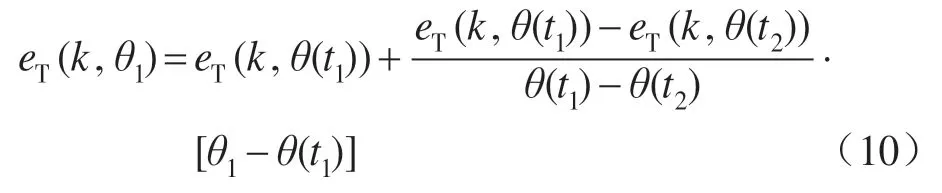
开环P型迭代学习运算公式为

式中:Kp是开环迭代学习系数。
在实际控制系统中,迭代学习控制器的输出是按采样时间规律作用到被控对象,但基于转子位置的迭代学习控制是按迭代位置点进行输出更新,为了得到各采样时刻点的迭代学习控制输出值,如图8 所示,通过相邻的θ1和θ2两个迭代位置点的位置角信息和迭代输出数据值u,采用下式的线性插补的方式,计算其间的各采样时刻点的迭代输出数据值。
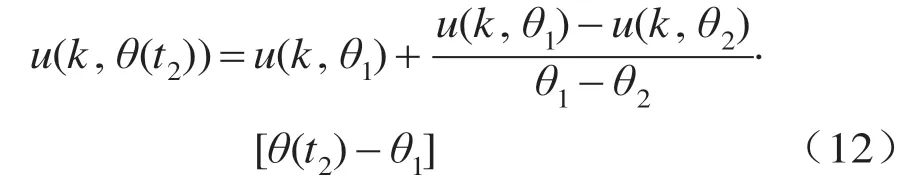
采用式(5)的立方分配函数f(θ),由总电流补偿量u 可计算关断相和开通相的参考电流补偿量,其计算公式分别为
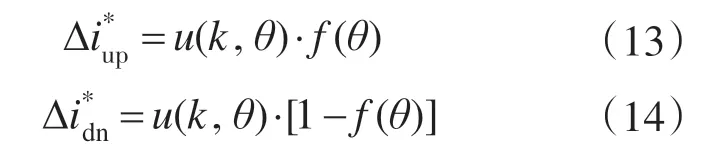
则开通相和关断相修正后的参考电流分别为
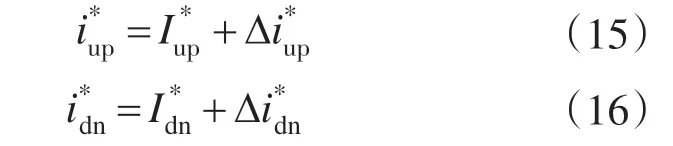
2.4 分区细化的电流滞环控制器的设计
电流控制器作为核心控制环节,必须满足参考电流的精确控制和快速跟踪的要求,借鉴文献[11]的转矩滞环控制策略,将不对称半桥功率转换器的开关状态定义为1,0 和-1 3 种工作状态,在仅使用1 和-1 两种状态的传统滞环控制策略基础上,设计了分区细化的电流滞环控制器。根据图9 所示的理想电流曲线特点,将电流曲线分成开通区、单相导通区和关断区3个区段。

图9 参考电流曲线Fig.9 Profile of reference current
在开通区和单相导通区,电流曲线的变化相对较慢,为了提高电流跟踪精度,电流控制使用如图10a 所示的滞环控制策略,该策略的滞环控制逻辑为:若电流偏差大于ΔImax,则开关状态值为1;若电流偏差小于ΔImax且大于0,则开关状态值为0;若电流偏差大于-ΔImax且小于0,则开关状态值为0;若电流偏差小于-ΔImax,则开关状态值为-1;该滞环策略可以有效提高电流控制效果,但是电流跟踪速度相对较慢。
在关断区,为实现电机快速换相,电流要快速减小到零,电流曲线下降较快,为保证电流能够被快速跟踪,在该区间使用如图10b 所示的电流可快速调节的传统滞环控制策略,该策略的滞环控制逻辑为:若电流偏差大于ΔImax,则开关状态值为1;若电流偏差小于ΔImax且大于0,则开关状态值为-1;若电流偏差大于-ΔImax且小于0,则开关状态值为1;若电流偏差小于-ΔImax,则开关状态值为-1。
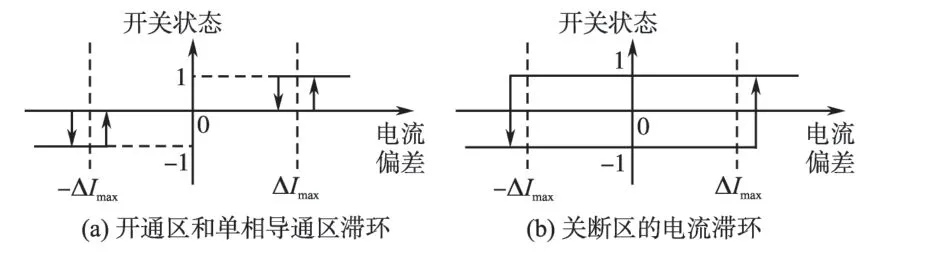
图10 分区细化的电流滞环控制器工作原理图Fig.10 Schematic diagram of current hysteresis controller with partition refinement
3 仿真验证与分析
为了验证本文提出的控制策略对SRM 非线性控制系统的适应性,在Matlab/Simulink 环境下,进行了仿真控制研究。仿真中,采用Simulink模型库中12/8 极结构的非线性SRM 模型[12],电机模型的主要参数设置[11]:最小电感值Lmin=0.67 mH,最大电感值Lmax=23.62 mH,定子绕组电阻阻值Rs=0.05 Ω,磁链最大值Ψmax=0.48 Wb;其他主要参数:直流电源电压VDC=100 V,电机负载TL=4.8 N·m,给定转矩Td=5 N ⋅m,电机稳态运行转速n=200 r/min。迭代学习算法相关参数:位置迭代周期为45°角,迭代学习系数Kp=0.5,迭代位置角步长Δθ=0.1°。为了衡量SRM的转矩脉动大小,采用文献[13]的转矩脉动系数定义:

式中:Tmax为最大瞬时转矩值;Tmin为最小瞬时转矩值;Tav为平均转矩值。
图11 是基于电流迭代学习的总转矩TSF 闭环控制结果,由转矩波形可知,电机总转矩可快速收敛到给定转矩,且收敛后的转矩脉动较小,稳态时的转矩脉动系数为1.73%。为了比较转矩脉动抑制效果,本文对传统TSF开环控制策略进行了仿真研究,转矩波形如图12 所示,其转矩脉动较大,转矩脉动系数为45.51%。仿真结果比较可知,本文提出的基于电流迭代学习的总转矩TSF 闭环控制策略有效地减小了电机的转矩脉动。

图11 基于ILC的TSF转矩闭环控制策略的转矩波形Fig.11 Torque curve of TSF torque closed-loop control strategy based on ILC
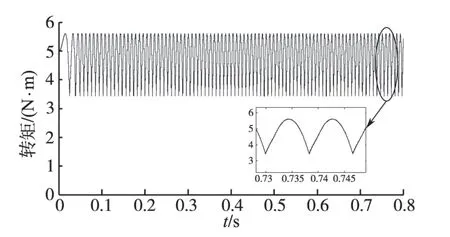
图12 传统TSF开环控制策略的转矩波形Fig.12 Torque curve of traditional TSF openloop control strategy
图13 a为迭代学习控制器输出的总电流补偿波形,通过立方分配函数计算分配得到图13b 的参考电流补偿波形,参考电流补偿值再叠加到图13c中补偿前的参考电流曲线,得到图13c中补偿后的理想参考电流曲线。对比图13c中迭代学习补偿前和补偿后的参考电流波形可知,补偿后的参考电流曲线具有SRM非线性特性,可修正简化的线性电感导致的转矩控制偏差,减小转矩脉动,得到图11所示的转矩脉动抑制控制结果。由图13d 的实际相电流波形可知,电流曲线周期变化,经过7~9个迭代周期,相电流波形基本不再变化,达到最佳电流曲线。
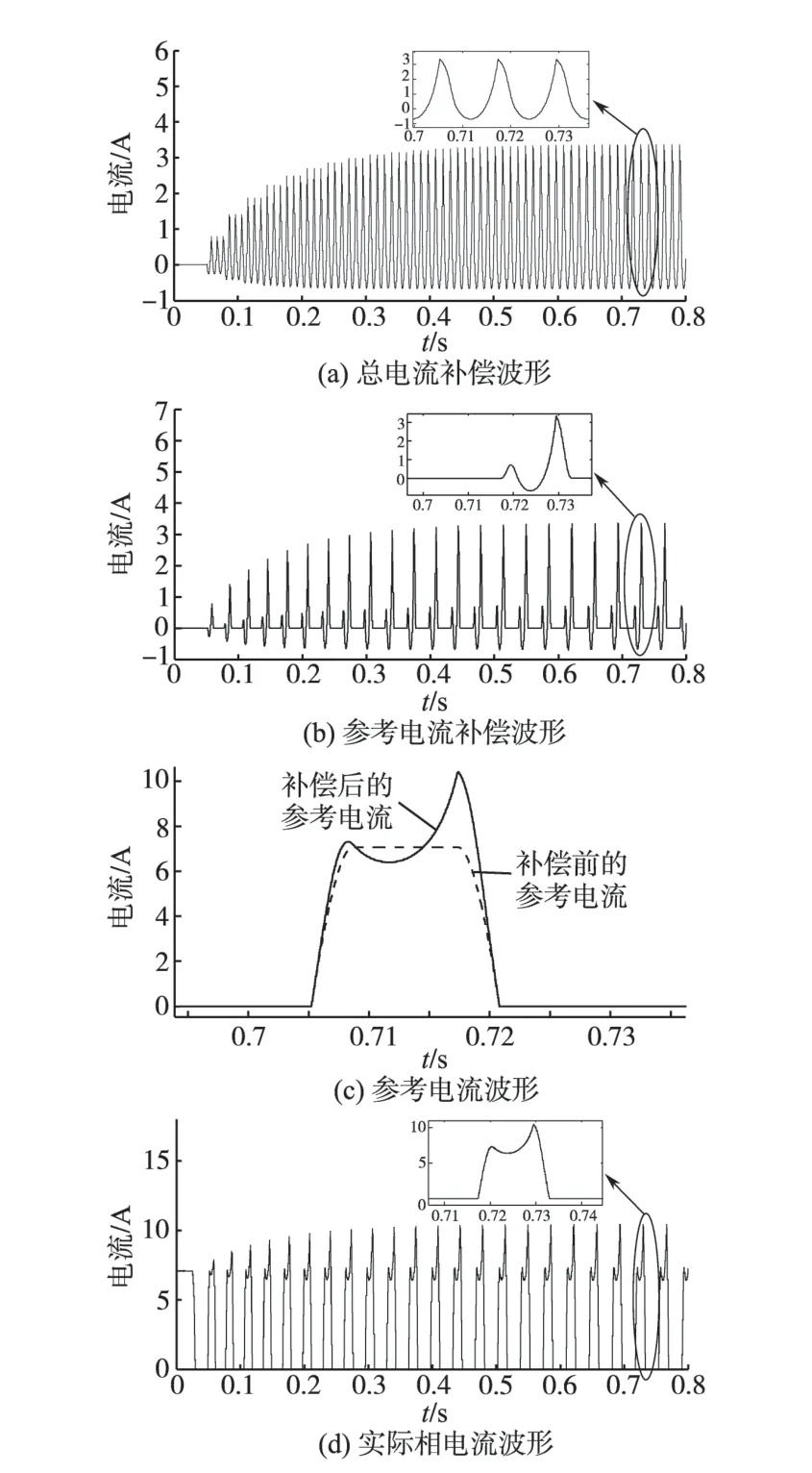
图13 基于ILC的TSF转矩闭环控制波形Fig.13 Curves of TSF torque closed-loop control based ILC
为了比较分区细化的电流滞环控制器和传统电流滞环控制器的控制效果,分别对其进行仿真研究,由图14a和图14b所示,分区细化电流滞环控制和传统电流滞环控制的转矩偏差对比波形与电流偏差对比波形可知,前者比后者的电流偏差小,相应的转矩偏差也较小,表1给出了分区细化电流滞环控制策略和传统电流滞环策略的转矩脉动数据。
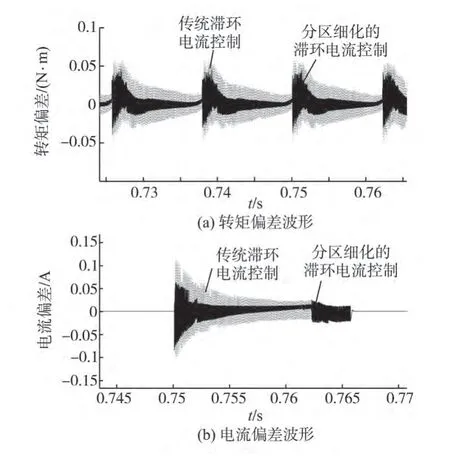
图14 传统滞环与分区细化的滞环控制波形Fig.14 Curves of traditional hysteresis control and hysteresis control with partition refinement
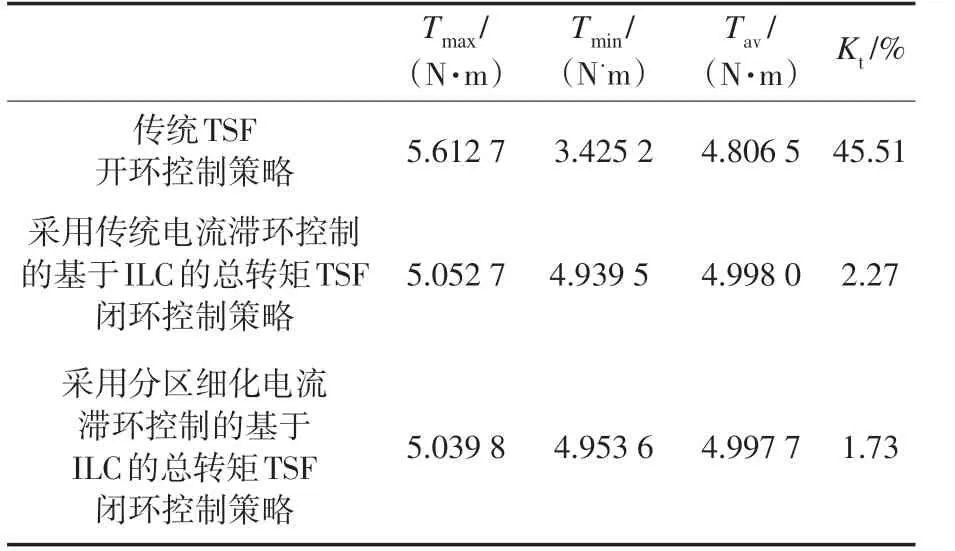
表1 转矩脉动系数Kt对比Tab.1 Comparison of toqrue ripple factor Kt
4 结论
本文在传统TSF开环控制策略基础上,引入电机总转矩负反馈,以迭代学习方式优化各相参考电流,使参考电流快速逼近最佳电流曲线,使用分区细化的滞环控制器对参考电流进行跟踪控制,达到抑制电机总转矩脉动的控制目标。仿真结果表明,提出的电流迭代学习优化的SRM总转矩TSF 闭环控制策略,对于给定转矩控制,转矩可快速收敛,稳态转矩脉动小,验证了所提出控制算法对转矩脉动抑制的有效性。应用中,如果电机瞬时总转矩不允许直接测量,可通过电机的电流和转子位置信息间接在线估算获得[14]。
[1] 周素莹,林辉.减小开关磁阻电机转矩脉动的控制策略综述[J].电气传动,2008,38(3):11-17.
[2] Jebarani Evangeline S,Suresh Kumar S.Torque Ripple Minimization of Switched Reluctance Drives-A Survey[C]//Power Electronics,Machines and Drives(PEMD 2010),5th IET International Conference on.IET,2010:1-6.
[3] Vrenken R H S,Duarte J L,Wijnands C G E,et al.Switched Reluctance Motor Drive for Full Electric Vehicles-part I:Analysis[C]//Power Eighth International Conference and Exhibition on Ecological Vehic1es and Renewable Energies(EVER),2013 8th International Conference and Exhibition on.IEEE,2013:1-7.
[4] Cheok A D,Fukuda Y.A New Torque and Flux Control Method for Switched Reluctance Motor Drives[J].Power Electronics,2002,17(4):543-557.
[5] 漆汉宏,张婷婷,李珍国.基于DITC的开关磁阻电机转矩脉动抑制仿真研究[J].系统仿真学报,2009,21(10):3133-3138.
[6] Changhwan Choi,Seungho Kim,Yongdae Kim,et al.A New Torque Control Method of a Switched Reluctance Motor Using a Torque-sharing Function[J].IEEE Transactions on Magnetics,2002,38(5):3288-3290.
[7] 吴红星.开关磁阻电机系统理论与控制技术[M].北京:中国电力出版社,2010.
[8] Sanjib K Sahoo,Sanjib K Panda,Xu Jian Xin.Indirect Torque Control of Switched Reluctance Motors Using Iterative Learning Control[J].IEEE Transactions on Power Electronics,2005,20(1):200-208.
[9] Xue X D,Cheng K W E,Ho S L.Optimization and Evaluation of Torque-sharing Functions for Torque Ripple Minimization in Switched Reluctance Motor Drives[J].IEEE Transactions on Power Electronics,2009,24(9):2076-2090.
[10]Sahoo S K,Panda S K,Xu J X.Application of Spatial Iterative Learning Control for Direct Torque Control of Switched Reluctance Motor Drive[C]//Power Engineering Society General Meeting,IEEE,2007:1-7.
[11]党选举,袁小唐,胡景佳.基于柔性神经网络的SRM直接瞬时转矩控制[J].电气传动,2014,44(5):62-66.
[12]Cajander D,Le-Huy H.Design and Optimization of a Torque Controller for a Switched Reluctance Motor Drive for Electric Vehicles by Simulation[J].Mathematics and Computers in Simulation,2006,71(4):333-344.
[13]Iqbal Husain.Minimization of Torque Ripple in SRM Drives[J].IEEE Trans.on Industrial Electrtions,2002,49(1):28-39.
[14]Lin Z,Reay D S,Williams B W,et al.On-line Torque Estimation in a Switched Reluctance Motor for Torque Ripple Minimisation[C]//Industrial Electronics,2004 IEEE International Symposium on.IEEE,2004,2:981-985.

