基于改进混合核SVM的非线性组合预测
程双江 李世平 邬肖敏 郑 堂
(第二炮兵工程大学,西安 710025)
基于改进混合核SVM的非线性组合预测
程双江 李世平 邬肖敏 郑 堂
(第二炮兵工程大学,西安 710025)
针对SVM在预测过程中核函数难以确定的问题,采用混合核函数并进行改进,提出基于预测有效度的混合核函数混合参数确定准则;结合多项式预测和ARIMA预测单一预测模型,实现了改进的SVM用于某电压计量标准精度的非线性组合预测,结果表明改进后的SVM预测效果得到了很大程度的提高,具有很高的应用价值。
SVM;混合核函数;非线性组合预测;预测有效度
0 引言
预测是运用科学的判断方法,对事物未来可能演变的情况,事先作出推测的一种技术。传统的单一预测模型包括时间序列预测模型、回归分析预测模型、随机时间序列预测模型和灰色系统预测模型等[1-2],然而单纯的使用某一种单一预测模型往往达不到理想的预测精度,因此1969年Bates和Granger提出了组合预测[3]的概念。组合预测分为线性组合预测和非线性组合预测两种,线性组合预测是不同预测方法的值之间的一种凸组合,对于—个复杂系统的预测对象,单单依靠各个子方法的简单线性相加有时候会出现预测精度不高甚至无法预测的现象[4-5],因此本文采用基于SVM的非线性组合预测。
本文将首先分别使用多项式模型和ARIMA模型对某电压计量标准精度进行单一预测,而后将单一预测模型结果作为输入,输入到SVM进行组合。考虑到SVM核函数[6]选择的重要性,本文将采用多项式(poly)核和径向基(RBF)核的混合核[7-8]进行SVM非线性组合预测,这样即可以保证预测的拟合能力又能提高其外推性。但是考虑到截止到目前为止混合核函数的混合参数(各核函数所占百分比)的确定尚没有统一的有效方法,因此本文将预测有效度[9-10]引入到混合参数的确定当中,提出了一种基于预测有效度的混合核SVM组合预测模型,将其应用到某电压计量标准精度的预测当中进行分析。
1 单一预测模型
考虑到多项式模型对于趋势项拟合效果较好,而ARIMA模型对于随机序列效果较好,因此单一预测模型选择两者。
多项式模型是基于多项式的非线性拟合能力,对历史数据进行拟合和预测,多项式拟合的性能跟多项式阶数有很大的关系,多项式的阶数越高,拟合的效果越好,但是阶数过高,会导致外推性变差,因此采用多项式模型,阶数必须要着重考虑。同时ARMA模型处理的是平稳信号,而计量标准精度的变化展现出的是非平稳特性,因此首先要去非平稳化,即对信号进行差分处理,建立ARIMA模型,该模型对随机信号能进行有效预测,尤其能处理周期性变化的序列,且建模时所需数据量少。因此将多项式模型与ARIMA模型相结合,能很好的相互补充。
2 SVM和SVM核函数
2.1 SVM简介
SVM是根据Vapnik等人提出的统计学理论发展而来的。该学习机主要建立在两个理论基础之上:VC维理论和结构风险最小化理论[11-12]。SVM根据有限的样本信息,在学习能力和模型的复杂性之间寻找二者的平衡,使其具有更强的泛化能力。
SVM的最大特点在于它通过非线性变换将原问题映射到某个高维特征空间中的线性问题上进行求解。这个非线性变换通过SVM的核函数实现,这样根据SRM准则,SVM回归预测问题最终就可表示为一个二次规划问题,不存在局部极小点。
2.2 SVM核函数
对于SVM而言,不同的核函数和核函数参数,对预测结果起着决定性的作用,而核函数的种类有很多,常见的有多项式(poly)核函数、径向基(RBF)核函数和Sigmoid核函数等,因此选择何种核函数是研究SVM的重点。鉴于这些核函数在类型上可分为局部核函数和全局核函数,全局核函数具有较强的外推能力,局部核函数具有较强的拟合能力,因此本文采用混合核函数进行研究。
poly核函数和RBF核函数分别作为全局核函数和局部核函数的代表被运用到本文的混合核函数当中,其计算公式分别表示如下
Kpoly(xi,xj)=[(xi·xj)+1]d
(1)
式中,d为poly核函数的阶数;σ为RBF核函数的宽度。取xj=0.2,d分别为1、2、3,则poly核函数曲线图如图1所示,由图中我们可以清楚地看到poly核函数的全局性。
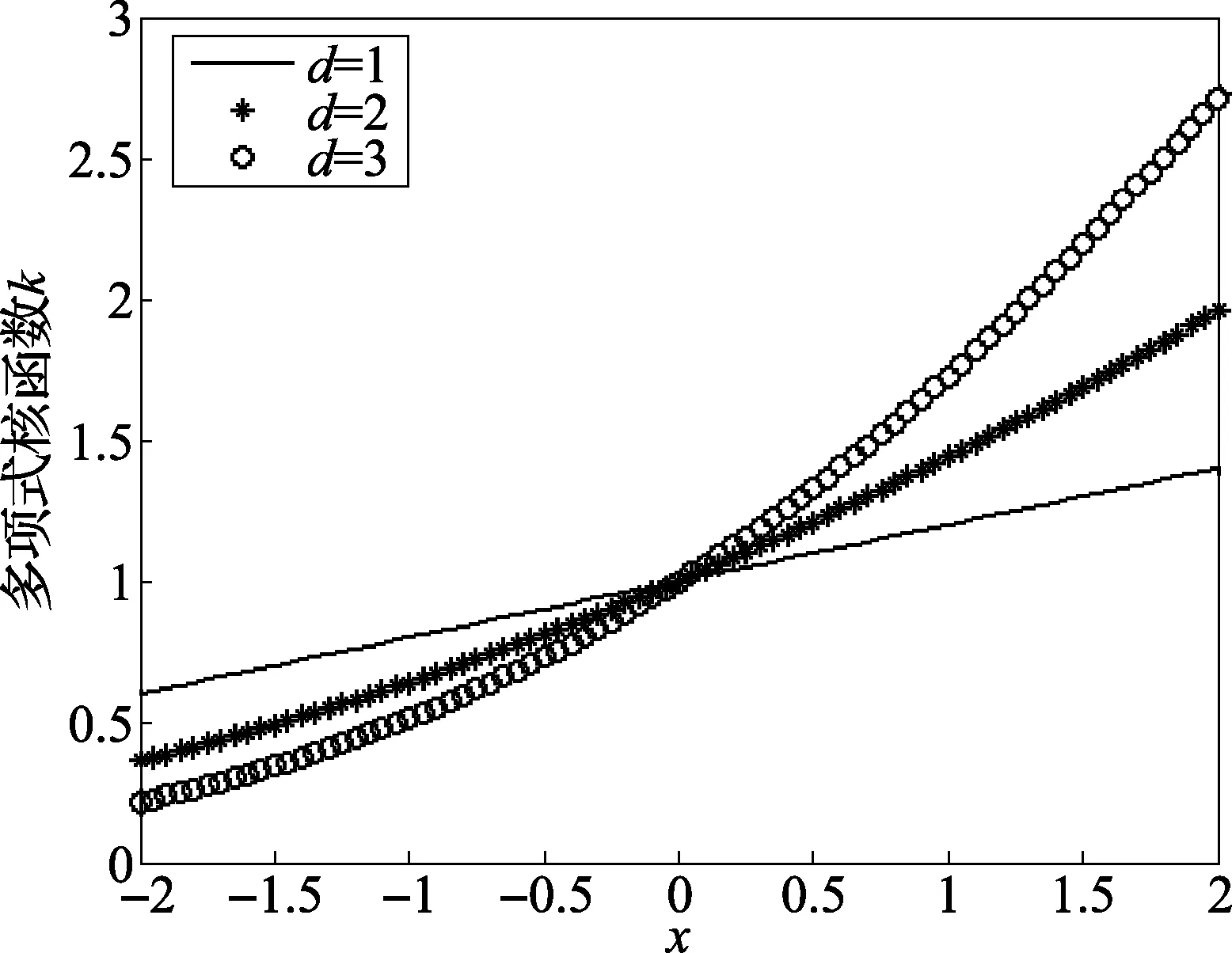
图1 poly核函数曲线
同样取xj=0.2,宽度σ分别取0.1、0.3、0.5,RBF核函数曲线图如图2所示,从图中我们可以发现RBF核函数值仅在测试点附近才较大,因此RBF核函数是局部核函数。
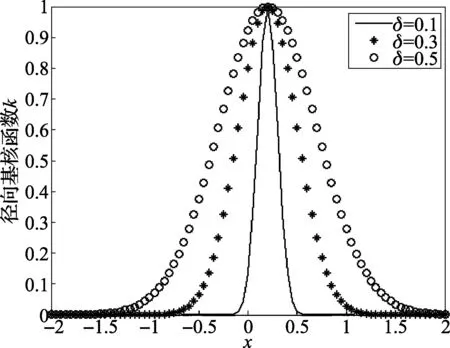
图2 RBF核函数曲线
3 基于预测有效度的混合核函数SVM
混合核函数指的是将两个不同的核函数混合起来使用,采用poly核和RBF核混合,混合后的核函数表述如下:
K=ρKpoly+(1-ρ)KRBF
(2)
式中,ρ为混合核函数混合参数,如何确定尚无定论。本文通过分析提出了一种基于预测有效度的方法。
预测有效度是基于对预测结果的评价,不同的指标序列具有不同的量纲导致无法直接进行比较而提出的。其定义如下:
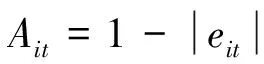
则第i种方法的k阶预测有效度可以表示为
(3)
其中H为某一k元连续函数。因此一阶预测有效度就可以用预测有效度元来表示,那么第i种预测方法在区间[N+1,N+T]上的一阶预测有效度就可表示为
(4)
那么基于一阶预测有效度的混合核函数参数ρ就可以按照下面公式确定
(5)
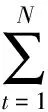
按照拟合误差“近大远小”[13]的原理,即区别对待各时刻的拟合误差,历史中近期的发展规律应该得到更好的拟合,远期历史数据的拟合程度可以稍低,取
(6)
将式(6)带入式(5)就可以求得混合参数ρ的大小。
4 基于预测有效度的混合核函数SVM组合预测实例分析
计量标准是保障仪器测量量值准确、统一的物质基础。对其进行精度预测是进行计量标准全寿命周期质量控制、管理与检测的主要手段,是科学合理的确定计量标准量值传递和溯源周期的重要依据,在确定仪器的有效使用时间和使用寿命方面具有重要的应用价值,这里将计量标准的精度预测转换成误差数据进行预测研究。
预测流程可以表示为如图3所示。
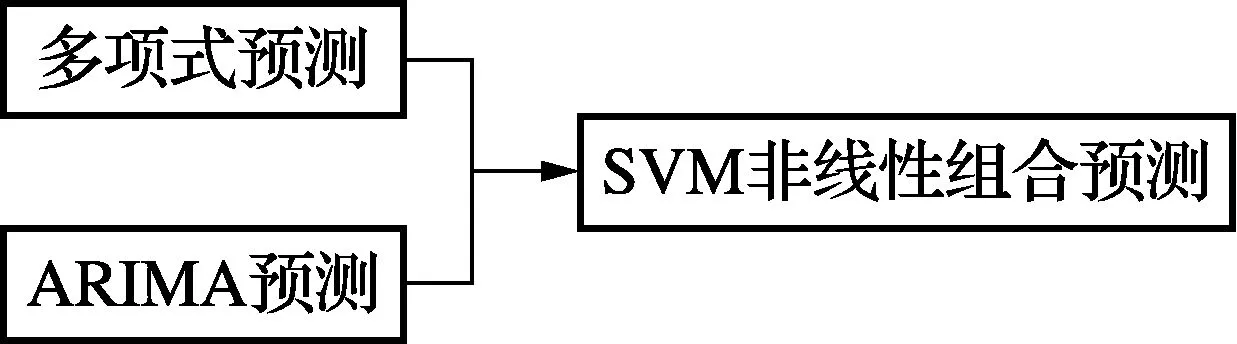
图3 预测流程图
预测步骤可表述如下:
步骤1):进行多项式模型和ARIMA模型的单一模型预测;
步骤2):根据单一模型的预测结果,分别进行多项式核和RBF核SVM的非线性组合预测;
步骤3):根据poly核和RBF核预测结果,计算混合核函数的混合参数;
步骤4):利用混合核函数进行SVM非线性组合预测。
本设计是基于某计量站2004年至2011年10V电压计量标准精度变化监测数据为依据,进行实例分析。监测数据如表1所示,共96个数据点,选取90个点作为样本进行拟合训练,剩余6个点进行预测分析。
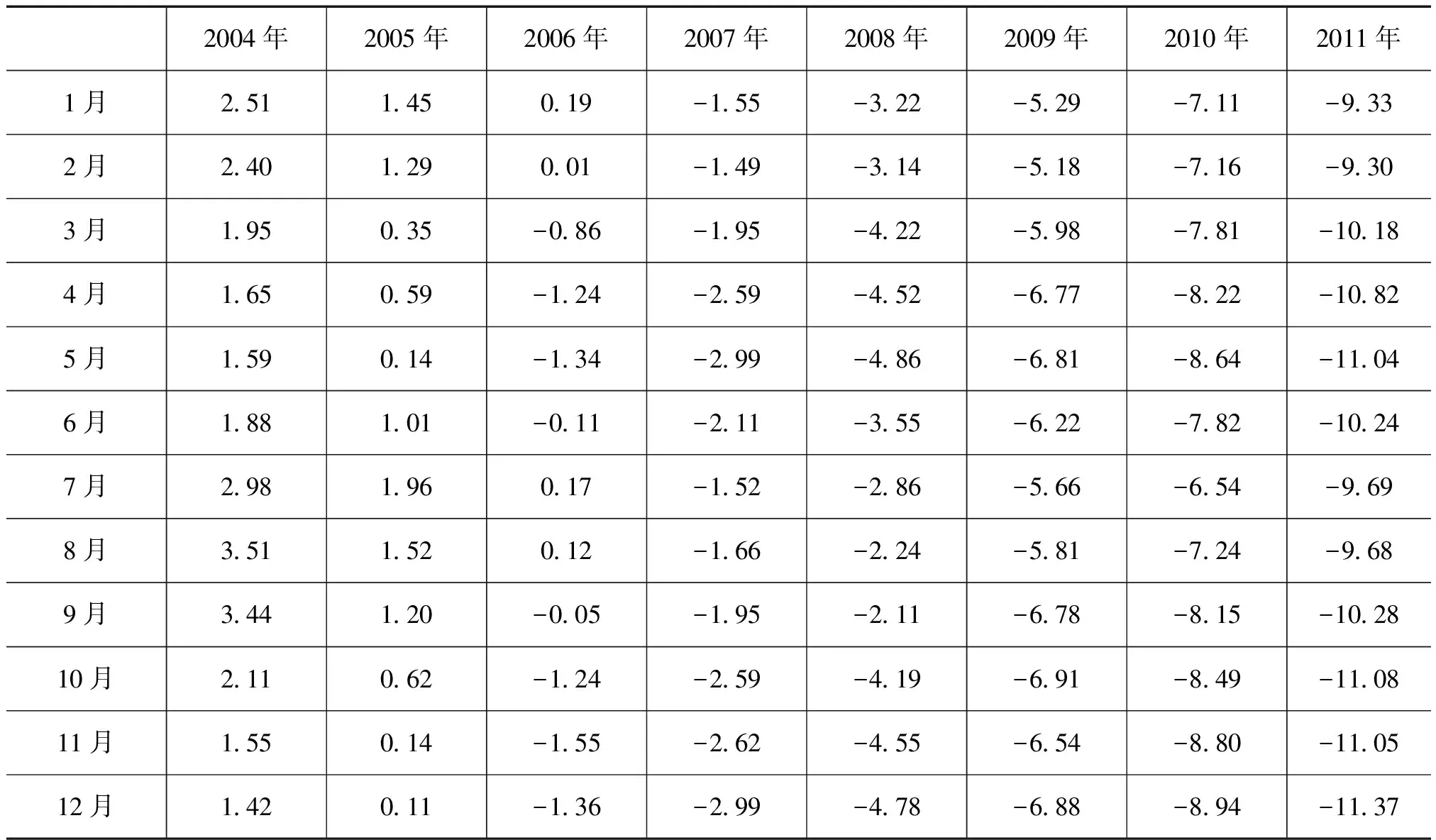
表1 10V电压计量标准精度变化监测数据 (单位:10-6V)
首先分别采用多项式模型和ARIMA模型进行单一模型预测,多项式模型阶数设为4,ARIMA模型的参数(p,d,q)分别取值为(4,5,1),预测结果如图4所示:
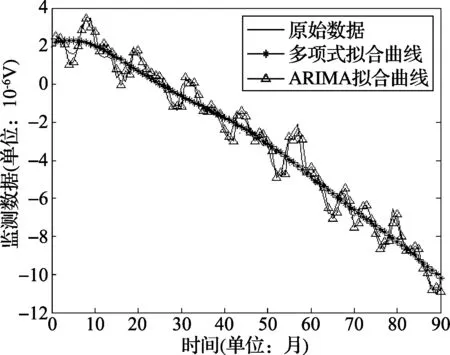
图4 多项式模型和ARIMA模型拟合
由图(4)我们可以看到,就本实例来说多项式模型和ARIMA模型均反映出了误差的变化趋势,ARIMA模型预测相对效果较好,但仍有较大误差。为了进一步的提高预测性能,我们进行SVM组合预测,为了提高预测精度,使用遗传算法(GA)对SVM的参数进行优化。首先分别使用poly核SVM和RBF核SVM进行非线性组合预测,而后根据两者的预测结果计算混合核函数的混合参数,最后使用设计的基于预测有效度的混合核SVM进行预测,分析比较预测结果。采用poly核和RBF核SVM进行预测的拟合曲线和误差曲线分别如图(5)和图(6)所示:
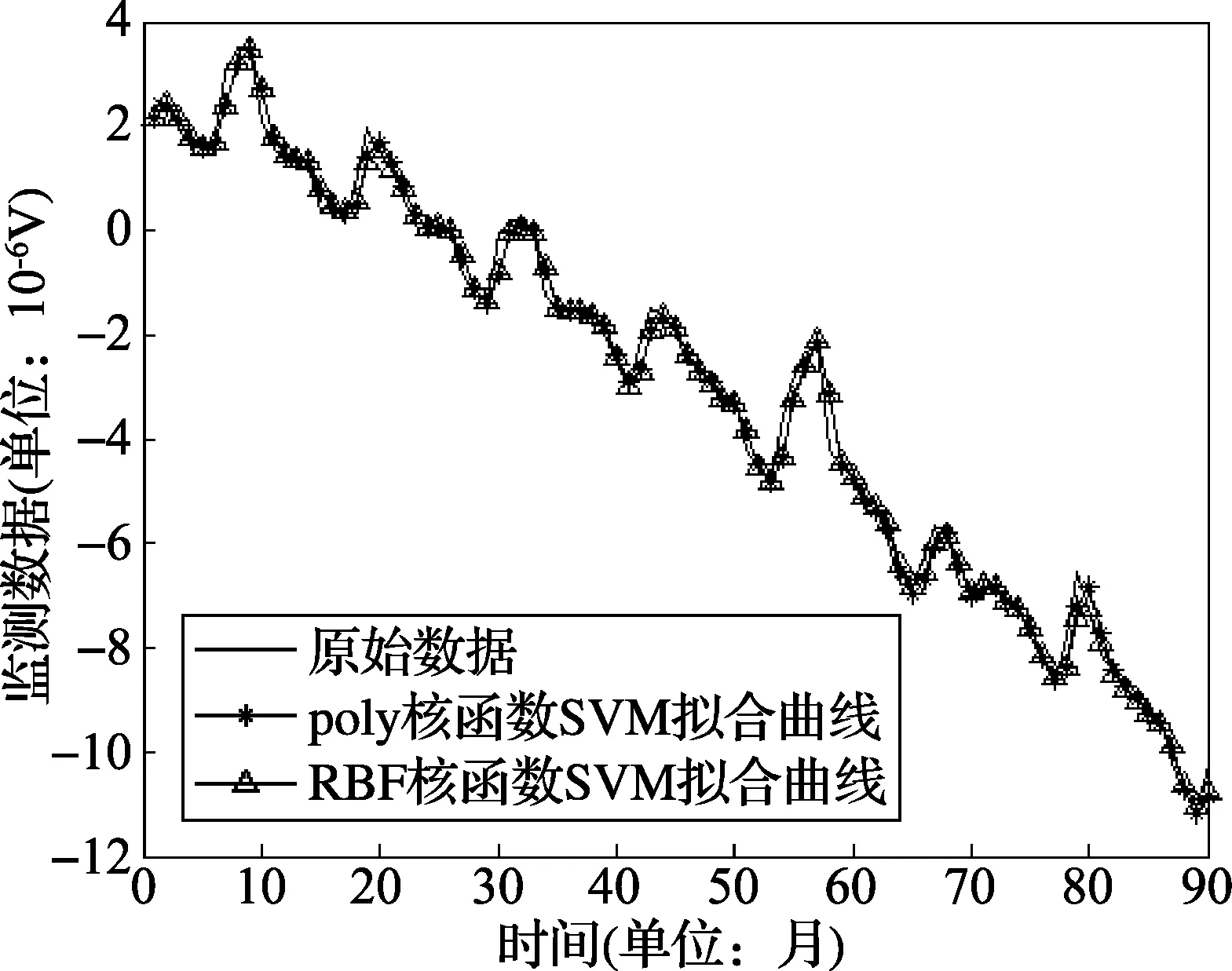
图5 poly核和RBF核拟合曲线
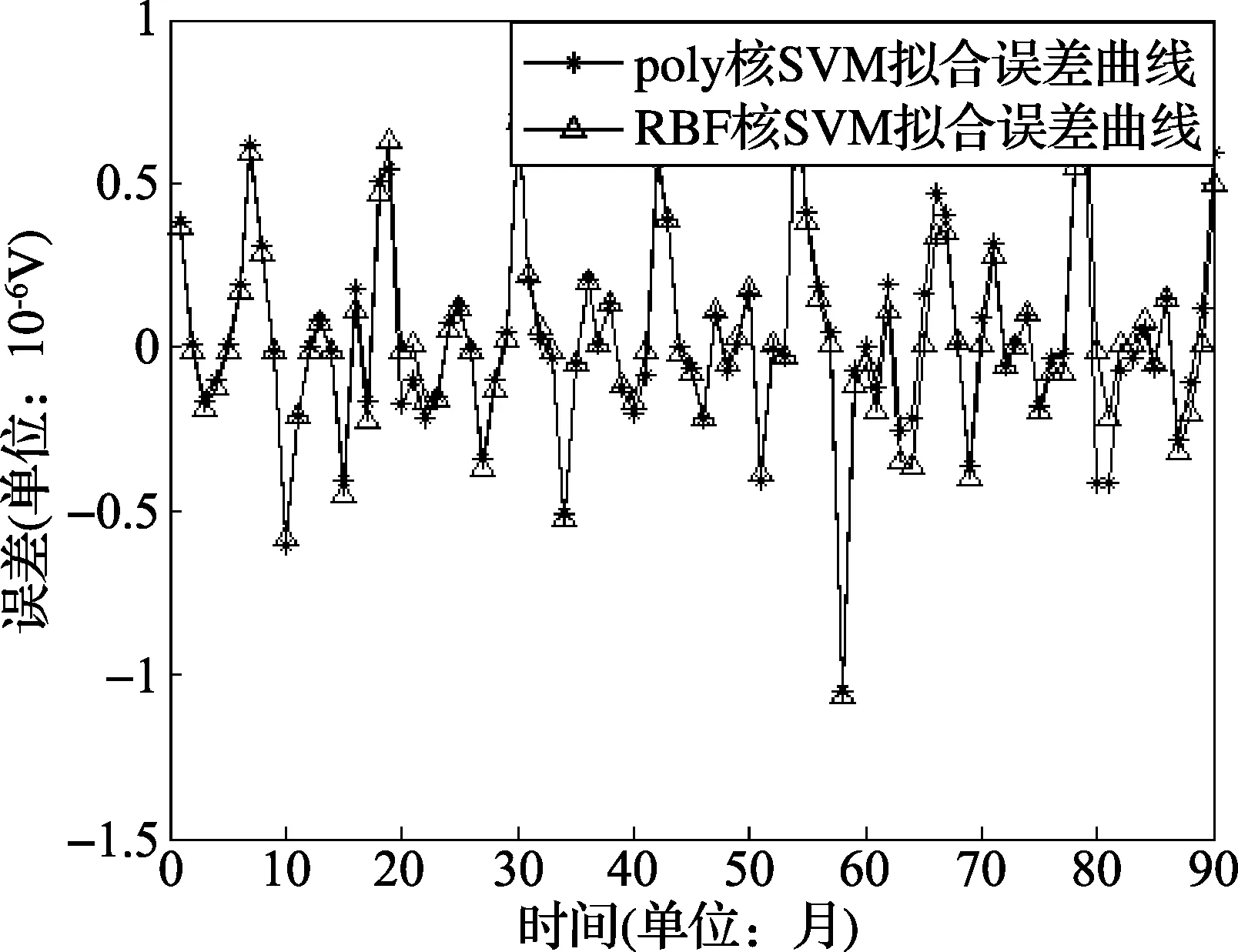
图6 poly核和RBF核拟合误差曲线
由图5和图6可以看到,组合预测SVM模型相比于多项式和ARIMA单一预测模型,精度得到很大程度的提高,反映了组合预测的强大优势。根据两者预测结果,经计算得混合核参数ρ=0.347,然后进行混合核SVM组合预测,得到拟合曲线(图7)和误差曲线(图8)如下所示。

图7 混合核SVM拟合曲线
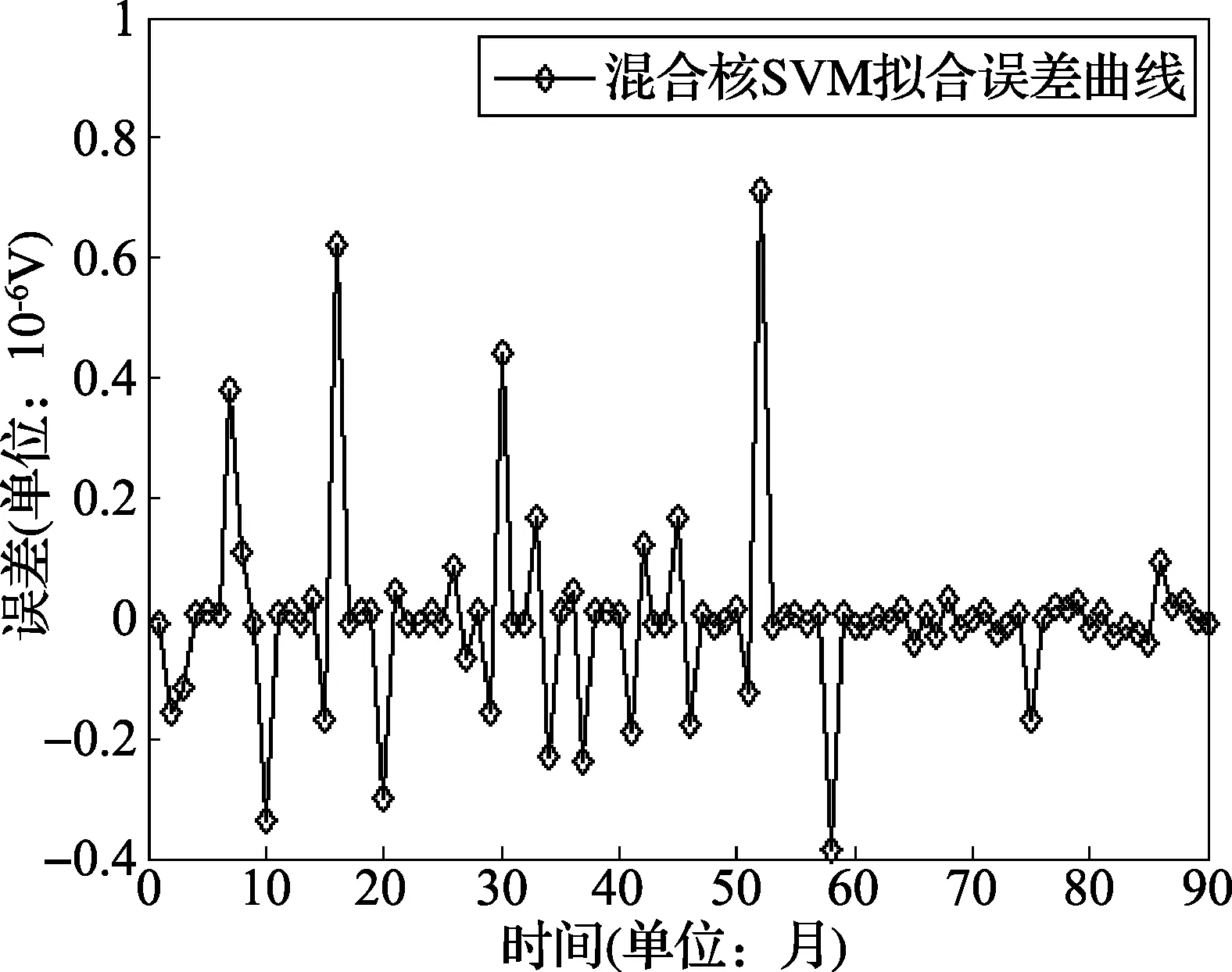
图8 混合核SVM拟合误差曲线
可以看到,基于预测有效度的混合核函数SVM预测相比单一核SVM预测性能又得到了进一步的提升。为了更加直观的看到效果,将两单一预测模型和三种不同形式核函数SVM分别用于后6个数据点的预测,6个数据点的实际值与预测值进行比较如表2所示。
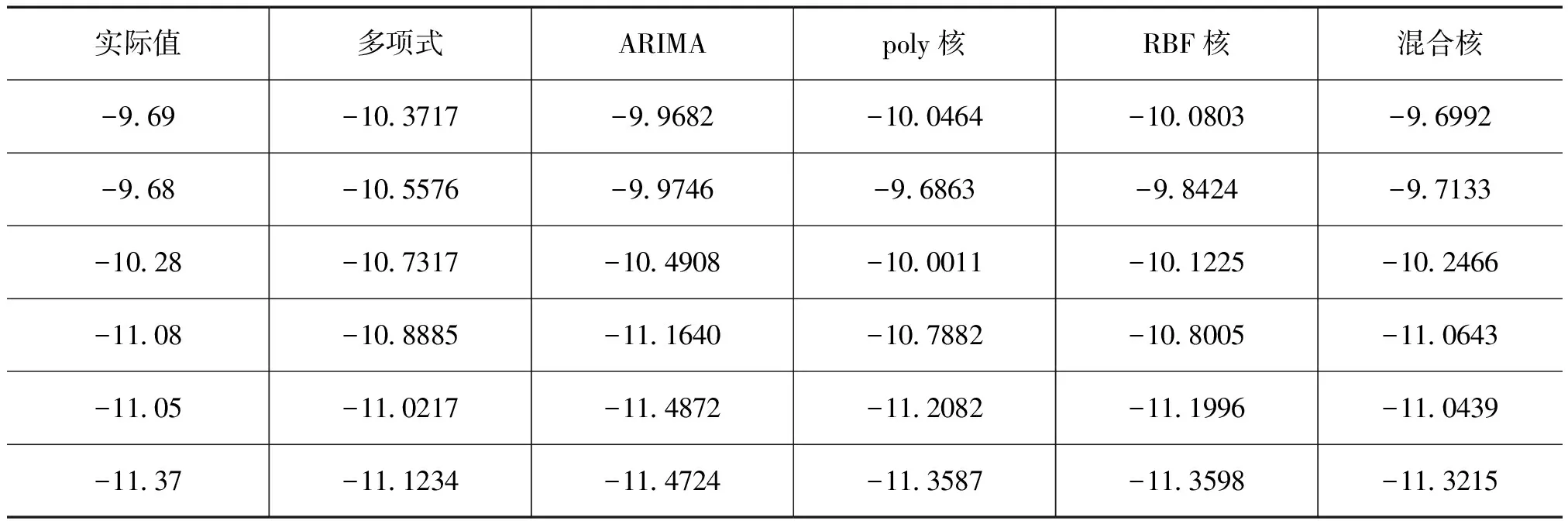
表2 不同核函数实际值与预测值比较 (单位:10-6V)
对于预测结果的评价,采用误差平方和作为准则,得到五种不同形式预测的评价结果如表3所示。
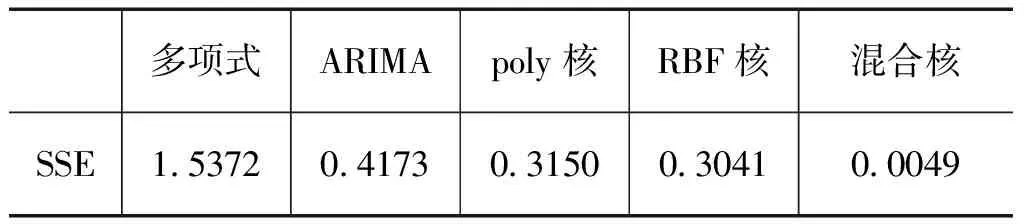
表3 预测结果评价 (单位:10-6V2)
可以发现,非线性的组合预测模型比单一预测模型预测精度得到很大程度的提高,经过改进后的混合核函数SVM相对于多项式核和RBF核SVM预测精度也得到了进一步的提升,效果比较明显。
5 结论
本文将预测理论引入到计量标准的预测当中,结合单一多项式模型和ARIMA模型,实现了基于SVM的10V电压计量标准的非线性组合预测,鉴于核函数的重要性,采用了混合核函数,并对混合核函数的混合参数提出了一种新的计算方案,结果表明此方法有效地提高了预测精度,可以考虑作为短期计量标准预测的方案。
[1] 唐小我,等.现代组合预测和组合投资决策方法及应用[M].北京:科学技术出版社,2003
[2] 鄢小彬.组合预测技术及其应用[D].武汉:武汉理工大学,2007
[3] Bates J.M.,Granger C.W.J.,The combination of forecasts[J].Operational Research Quarterly,1969,20(4):451—468
[4] 韩冬梅,等.线性与非线性组合预测方法研究[J].情报科学,2007,25(11):1672-1678
[5] 甘旭升,等.基于ARIMA与SVM的飞行事故组合预测方法[J].中国安全科学学报,2011,21(7):79-81
[6] 吴德会.基于最小二乘支持向量机的传感器非线性动态系统辨识[J].计量学报,2008,29(3)
[7] 孙俊清.电学军事计量标准精度预测技术研究[D].西安:第二炮兵工程学院,2008
[8] 郑志成,等.基于混合核函数PSO-LSSVM的边坡变形预测[J].岩石力学,2012,33(5):1421-1425
[9] 冯新刚.支持向量机核函数的选择方法探讨[D].江西:江西理工大学,2012
[10] 陈华友.组合预测方法有效性理论及其应用[M].北京:科学出版社,2008
[11] 陈华友,侯定丕.基于预测有效度的组合预测模型研究[J].预测,2001,20(3):72-73
[12] 张凯,沙锋.基于非线性组合方法的石油期货价格预测研究[J].计算机仿真,2012,29(7):379-382
[13] 康重庆,等.电力系统负荷预测[M].北京:中国电力出版社,2008
10.3969/j.issn.1000-0771.2015.10.01

