雾霾环境的反应扩散模型及其最佳测量位置
钱 学 明
(无锡科技职业学院物联网与软件技术学院,江苏 无锡 214028)
雾霾环境的反应扩散模型及其最佳测量位置
钱 学 明
(无锡科技职业学院物联网与软件技术学院,江苏 无锡 214028)
讨论区域雾霾环境中传感器测量位置的优化问题。针对一类雾霾环境的反应扩散模型,利用Laplace变换,获得系统的解析解。基于优化估计理论,提出带测量噪声时系统监测传感器的最佳测量位置的优化方案。最后,数值例子表明了结论的有效性。
反应扩散模型;雾霾环境;Laplace变换;传感器;优化测量
近年来,由于现代工业的迅速发展,大气污染问题正日趋严重。中国的华北、黄淮、江淮和江南地区都出现了大范围的雾霾天气。雾霾的出现使得空气质量变差,城市视野模糊不清,已经严重地影响了人们的健康和日常生活。研究发现,大气污染主要来自三个方面:工厂废气的排放、交通工具的尾气以及日常的生活垃圾。尤其是大量污染物排向大气,使得大气的成分正在发生变化。因此,大气污染的监测、控制及预防成为研究中的焦点。其首要任务就是建立有效的监测系统。
为此,面临两个问题。一是什么样的模型可以用来描述大气污染?二是如何有效地监测大气污染?不难发现,污染在大气中的输运过程呈现为一个扩散过程。此类过程的特点是系统的状态不但依赖于时间而且依赖于空间,并且展示出其复杂的动力学特征。Varotsos等通过对某一地区污染状况的测量,利用实际数据,分析大气污染过程[1]。陈英杰等[2]基于扩散过程的动力学分析,建立了大气污染的三维反应扩散模型,并利用分离变量法给出了模型的解析解。该研究表明,将雾霾过程建模为反应扩散方程可以更加真实地模拟出污染物的扩散对大气的影响。近年来,对抛物型扩散系统的研究吸引了众多专家学者。Fridman等[3]利用静态传感器网络,通过设计输出反馈控制器,研究了一类半线性扩散方程的镇定问题。周璇等[4]通过研究分布参数系统中传感器位置的优化问题,提出了一类反应扩散系统的参数辨识方法。Qian[5,6]进一步研究了大气污染的反应扩散模型及其移动控制下的优化监测方案。
本文针对一类区域雾霾环境的反应扩散模型,利用Laplace变换,获得系统的解析解。从而,提出带测量噪声时系统监测传感器的最佳测量位置的优化方案。相较于此前的研究,Laplace变换使得系统状态解析解的求解更为简单且易于计算,同时也可结合相关软件,如MATLAB等。而反应扩散系统中传感器位置的优化估计也鲜见于现有文献。因此,研究雾霾环境的反应扩散模型及其最佳测量位置具有一定的实际意义和理论价值。
1 系统描述
我们考虑一类反应扩散模型描述的区域雾霾天气
(1)
且满足初始条件
ρ(x,0)=φ(x)
和Dirichlet边值条件
ρ(0,t)=ρ(l,t)=0
其中x表示一维空间位置,0≤x≤l,时间t>0,ρ(x,t)表示雾霾环境中x处、时刻t时污染物的浓度,D为扩散系数,α>0为吸收衰减系数。
不失一般性,本文对初始条件给出以下假设:

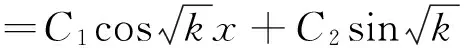
2 基于Laplace变换的系统模型的求解
Laplace变换是信号分析和电路求解的有效工具,可用于求解微分方程。为了求解区域雾霾环境的反应扩散模型(1),引入Laplace变换的概念。
Laplace变换的性质[7]
(1)线性性质
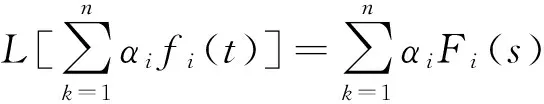
(2)微分性质
设L[f(t)]=F(s),则有L[f′(t)]=sF(s)-f(0)。
以下,将利用Laplace变换及其性质求解区域雾霾扩散的抛物型系统。
定理1 若系统初始值ρ(x,0)=φ(x)满足假设1,则区域雾霾的反应扩散模型的解为ρ(x,t)=e-(α-kD)tφ(x)。
证明:由于x的变化范围是[0,l],而t的变化范围是[0,+∞)。因此,该定解问题应当关于t取Laplace变换。ρ(x,t)满足Laplace变换存在定理,故可记L[ρ(x,t)]=U(x,s)。

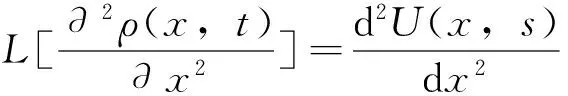
这样,原定解问题转化为含有参数s的二阶常系数线性微分方程的边值问题
(2)
其边值条件为
U(0,s)=U(l,s)=0
由二阶常系数线性微分方程的一般解法可得其通解为
其中U*(x,s)为方程的特解。
由边界条件,可知
c1=c2=0,U(x,s)=U*(x,s)
设U*(x,s)=G(s)φ(x),则(2)式可化为
根据假设1,可得
从而
对U(x,s)取Laplace逆变换,则原定解问题的解为
ρ(x,t)=e-(α+kD)tφ(x)
注2:由定理1不难发现,系统(1)是全局指数稳定的。
推论1 若系统初始值ρ(x,0)=φ(x)满足假设1且α=0,则区域雾霾的反应扩散模型的解为ρ(x,t)=e-kDtφ(x)。
推论2 若系统初始值ρ(x,0)=αsin(βx)+bcos(βx),则区域雾霾的反应扩散模型的解为ρ(x,t)=e-(α+β2D)t(αsin(βx)+bcos(βx))。
3 测量位置最优化
对于区域雾霾的反应扩散系统,系统的N个测量输出可以写成以下形式
y(x,t)=Bρ(x,t)+ν(x,t)
(3)
其中y(x,t)=[y1(x,t),y2(x,t),…,yN(x,t)]T为系统N个传感器的测量输出,B=[b1,b2,…,bN]T为系数向量,ν(x,t)=[ν1(x,t),ν2(x,t),…,νN(x,t)]T表示不同位置的测量噪声。不失一般性,本文考虑ν(t)满足以下假设。
假设2 测量噪声ν(t)为独立分布的白噪声,且满足
E{ν(x,t)}=0,E{ν(x,t)νT(x,τ)}=Q
为了得到传感器的最优测量位置,将系统测量输出在x=x0的领域内线性化。于是,(3)式的泰勒公式可写为
(4)
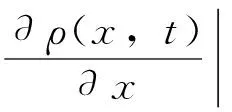
(5)
yd(x,t)=η(x0,t)x+ν(x,t)
(6)
因此,可以设输出误差平方准则函数为
其中为P加权矩阵。
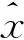
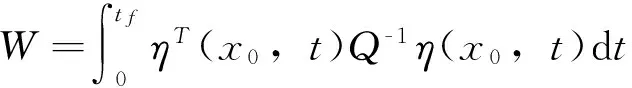
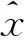
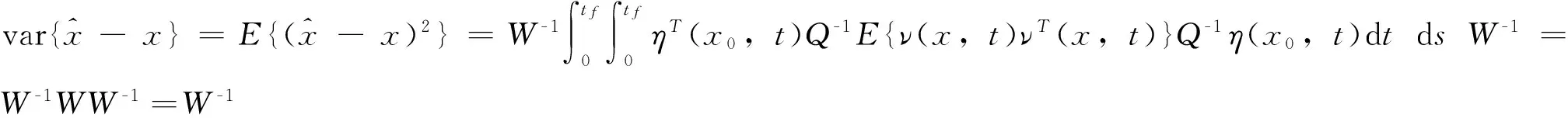
通过以上分析可知,W与静态传感器的最佳测量位置x0有关,且其取最大值时位置估计误差的方差最小。因此,使W取得最大值的x0即为所求最佳测量位置。
4 数值例子
以反应扩散模型为例,分析区域雾霾监测系统传感器位置的优化测量位置。
考虑一维反应扩散方程如下:
其中扩散系数D=0.04,且满足初始条件和边值条件分别为
ρ(0,t)=ρ(π,t)=0。
根据推论2,不难得到系统模型的解析解为
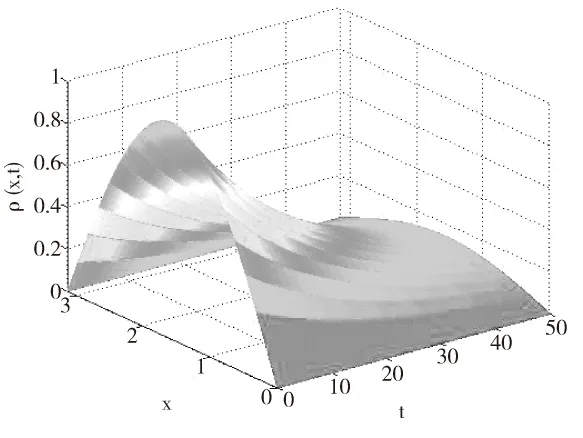
图1 雾霾浓度的时空分布
在空间[0,π]上一静态传感器测量输出为
y(x,t)=ρ(x,t)+ν(x,t)
其中ν(x,t)零均值且Q=I。
设静态传感器的最佳测量位置在x1处,考虑
计算可得,

当x1=0.049 9时,W最大。

图2 雾霾浓度的时空分布的等高线
于是,根据定理2可知,x1=0.049 9为静态传感器的最佳空间测量位置。
注3:该例仅考虑一个测量点的情形,当测量点的个数大于2时,则需考虑使用D-最优试验设计的数值方法[9]。
5 结 论
本文主要讨论了一类区域雾霾环境的反应扩散模型及其最佳测量位置的选择。针对雾霾反应扩散系统,利用Laplace变换方法,获得了系统状态的解析解。由此,基于优化估计理论,提出了带测量噪声时系统中监测传感器的最佳测量位置的优化方案。通过数值仿真表明,文中的结论符合实际且应用方便。
[1]Varotsos C,Kondratyev K,Efstathiou M.On the seasonal variation of the surface ozone inathens[J].Greece Atmosph Environ,2001,35(02):315-320.
[2]陈英杰,刘玉良,刘萍.三维大气污染反应扩散方程模型[J].哈尔滨师范大学自然科学学报,2014,30(05):1-3.
[3]Fridman E,Blighovsky A.Robust sampled-data control of a class of semi-linear parabolic systems[J].Automatica,2012,48(05):826-836.
[4]周璇,喻寿益,李兰君,高崧.分布参数系统中传感器位置的优化[J].中南大学学报:自然科学版,2003,34(04):398-401.
[5]Qian X.Optimal monitoring in reaction-diffusion model of the atmospheric pollution[J].J Simul,2015,3(02):3-6.
[6]Qian X,Cui B.Mobile sensor networks for sampled-data control of a class of distributed parameter systems[A].The 26th Chinese Control and Decision Conference(2014 CCDC)[C].IEEE,2014:3735-3738.
[7]张元林.《积分变换》(第四版)[M].北京:高等教育出版社,2003.
[8]T.C.His.系统辨识与应用[M].长沙:中南工业大学出版社,1986.
[9]Tricaud C,Patan M,Uciriski D,et al.D-optimal trajectory design of heterogeneous mobile sensors for parameter estimation of distributed systems[J].Proceed Amer Control Conf,2008:663-668.
[责任编辑:王荣荣 英文编辑:刘彦哲]
Diffusion-Reaction Model and Optimal Sensing Location of Smog
QIAN Xue-ming
(School of Internet of Things and Software Technology,Wuxi Professional College of Science and Technology,Wuxi,Jiangsu 214028,China)
Optimal sensing location is considered for the diffusion-reaction model of smog.By using Laplace transformation,the analytic solution of diffusion-reaction system is obtained.Under the measurement output of system with sensor noise,an optimal sensor location scheme is proposed based on the theory of the optimal estimation.Finally,a numerical example is given to show the effectiveness of results.
reaction-diffusion equation;smog;Laplace transformation;sensor;optimal monitoring
江苏省自然科学基金(BK20131109);无锡市软科学研究课题项目(KX14-B-13);无锡科技职业学院大学生实践创新训练计划立项项目(2014-13)
钱学明(1981-),男,江苏无锡人,无锡科技职业学院物联网技术学院讲师,博士,主要从事分布参数系统建模与优化控制研究。
X 502
A
10.3969/j.issn.1673-1492.2015.05.007
来稿日期:2015-09-08

