M LS地面设备检验平台距离测量的不确定度分析

程翊昕

陕西西安中国电子科技集团公司第二十研究所

M LS地面设备检验平台距离测量的不确定度分析

程翊昕

陕西西安中国电子科技集团公司第二十研究所

本文基于全站仪距离测量的原理，建立了相关不确定度分析和评定的数学模型。经过分析和计算DME天线距离测量的各个不确定度分量，得出了MLS地面设备距离测量的不确定度。

天线；距离；不确定度

引言

MLS地面设备检验平台需要测量接收/发射天线相对于被测设备的MLS的距离数值。用这个数值与距离测量单元测得的真值比较后，可得出MLS的地面设备误差。所以，有必要对MLS地面设备检验平台的距离进行测量。

在实际工程中，我们使用全站仪测量方位天线靶标的坐标及接收天线靶标的坐标，通过下述方法计算得到距离度值，为保证精度可多次测量，获得平均值。

-2147483648.测量方法

测量距离时，使用距离天线罩（即DME天线）的物理中心来代表距离天线的相位中心，方法示意图如图1。

使用全站仪对天线进行位置定标，获得了2组数据：距离天线中心（L1，θ11，θ12），接收天线（L2，θ21，θ22）。将其分解到同一水平面上，如图2所示：

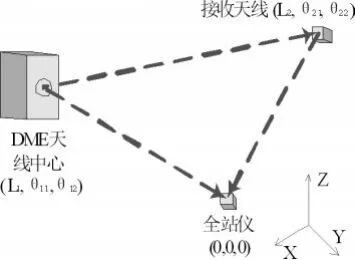
图1 .距离测量示意图

图2 .距离数据详细分解图

如图，其中：

l1=L1*cosθ11

H1=L1*sinθ11

l2=L2*cosθ21

H2=L2*sinθ21

仰角天线到接收天线水平距离

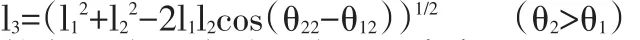
仰角天线和接受天线的垂直高差：

H=H2-H1（H2>H1）

得到DME距离：

-2147483648.计算各分量标准不确定度

A类不确定度的评定

在距离连续测量10次得到一组测量结果如下：

338.7517 m，338.7525m,338.7527m，338.7523m，338.7519m，

338.7530 m，338.7512m，338.7521m，338.7520m，338.7523m，计算出算术平均值的实验标准偏差s(xˉ)=0.00017m,标准不确定度uA=xˉ=0.00017m

B类不确定度的评定

位置基准测量中，会被引入的B类不确定度分量有两种：

1.测量时是DME天线罩的几何中心和接收天线的几何中心进行测量，但实际天线相位中心和天线罩物理中心不在同一点而引入的不确定度分量，可分为高度不一致，前后不一致，和左右不一致引入的三个分量；

2.全站仪测量不准引入的不确定度分量，可分为距离测量不准、方位角测量不准和仰角测量不准三个分量；

实际测量时单次测量距离以及计算得出的数据为：

xˉ=338.7522m，根据公式s(xˉ)=

L1θ12θ11L2θ22θ21θ22-θ12194.391m 28.189°0.14°159.443m 174.447°0.519°2.55139 l1H1l2H2l3HL3194.3904m 0.474986m 159.4365m 1.444256m 338.750306m0.96927m 338.75169m

根据上述数据计算测量不确定度分量。

DME天线相对于接收天线相位中心和天线罩物理中心高度不一致引入的不确定度分量

该分量在DME距离计算表达式中影响变量为H，则：

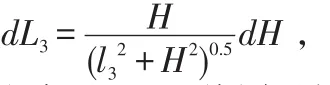
根据DME天线罩及接收天线实际大小估算得到，DME天线高度不一致引入的不确定度为0.03m，接收天线高度不一致引入的不确定度为0.01m，则：uB1=0.03+0.01=0.04m

DME天线相对于接收天线相位中心和天线罩物理中心前后不一致引入的不确定度分量

该分量在DME距离计算表达式中影响变量为l3，，根据DME天线罩及接收天线实际大小估算得到，DME天线前后不一致引入的不确定度为0.03m，接收天线前后不一致引入的不确定度为0.01m，则：uB2=0.03+0.01=0.04m

DME天线相对于接收天线相位中心和天线罩物理中心左右不一致引入的不确定度分量

全站仪距离测量不准引入的不确定度分量

该分量在DME距离计算表达式中影响变量为L1和L2。

由于全站仪相对于天线的距离远大于天线高度，为简化计算，可将该分量在DME距离计算表达式中影响变量视为l1和l2，则：

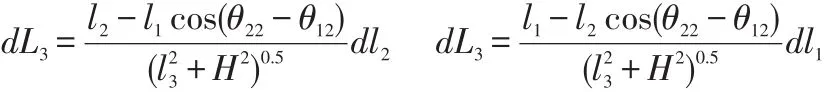
根据全站仪技术指标，距离测量最大允许误差为0.01m+距离×10-5，以200m计算得

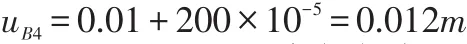
全站仪方位角测量不准引入的不确定度分量

根据全站仪技术指标，角度测量的最大允许误差为0.0003°，实际测量时距离小于200 m，换算为距离误差为200 m，200m×tan0.0003∘=0.001m，远小于天线中心不一致引入的不确定度分量，可忽略不计。

全站仪仰角测量不准引入的不确定度分量

该分量与2.2.5一样，可忽略不计。

合成标准不确定度

由DME距离计算式可得：

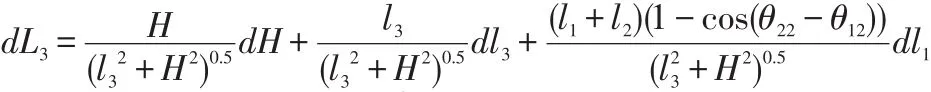
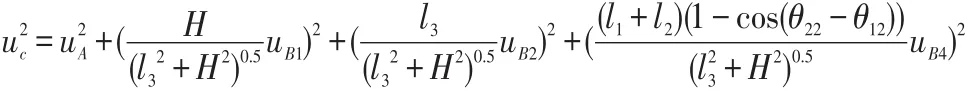
计算得出：uc=0.046m

扩展不确定度

取k=2，则U=0.092m。

结束语

通过不确定度合成发现，DME天线相对于接收天线相位中心和天线罩物理中心前后不一致引入的不确定度分量对测量结果影响最大，实际测试中应尽量减小该不确定度分量，以保证距离测量准确度。

[1]蒙特卡罗法在复杂模型测量不确定度评定中的应用仪器仪表学报王伟、宋明顺

[2]基于软件无线电架构的ENM通用测试模型与不确定度分析电子测量技术姚国英、孙路平

[3]基于量值特性的ATS动态测量不确定度评定国外电子测量技术薛庆文、孙中权、张华锋