基于样本熵的降雨和径流时间序列突变检验

薛联青刘远洪张梦泽王思琪李军

摘要：传统的突变检验方法MannKendall法主要基于线性和概率统计理论，对于高度复杂和非线性的水文时间序列检测能力不足。采用基于非线性动力学参数的样本熵方法，结合滑动技术和滑动移除技术，利用湘江流域1961～2009年多个气象站点日降雨资料和控制站湘潭站日径流资料，对降雨和径流时间序列进行突变检验。结果表明：日尺度降雨和径流时间序列样本熵值最小，复杂度最低，可预测性最高；径流分别在1966年、1983年、1992年以及2002年发生突变，降雨在1966年、1987年以及2002年发生突变；滑动样本熵与滑动移除样本熵相结合不仅能有效地识别突变，更能发现突变前后时间序列的动力学变化特征。

关键词：工程水文学；时间序列；突变检验；MannKendall法；样本熵；复杂度；湘江流域

中图分类号：P333；TV211.1文献标志码：A

0引言

由于气象条件的变化和人类活动的影响，流域下垫面发生了变化，水文系统循环时空范围与尺度发生了改变，造成了水文时间序列的时空变异[13]，而降雨和径流作为水文系统的重要组成部分，其长期变化趋势及突变常与自然灾害相伴生，带来了一系列诸如水文极值事件、洪涝灾害、严重干旱频繁发生等新问题，破坏了水文时间序列的一致性，给人类生产和生活带来不利影响。因此，研究变化环境下的降雨和径流时间序列变异规律，对于研究水资源的演变规律以及治理与合理开发利用水资源具有重要的现实意义。水文时间序列具有高度复杂性、非稳定性、非线性等特征，而传统的突变检验方法主要从线性和概率统计方面进行研究[45]，不能有效识别非线性的时间序列特征和变异前后时间序列的状态趋势，检测能力也不足。随着非线性理论的发展，20世纪90年代初，Pincus首次提出用近似熵[6]计算时间序列复杂度，并在各领域得到广泛应用[710]。2000年，Richman等对近似熵进行修正，提出样本熵（Sample Entropy，简称SampEn），旨在降低近似熵的误差，是一种与近似熵类似但精度更好的方法[11]；该方法被国内外学者广泛应用于降雨和径流时间序列的复杂度分析[1217]。2011年，何文平等提出滑动移除近似熵进行突变检测，其结果优于滑动近似熵[18]。杜鹃等采用MannKendall法（简称MK法）对湘江流域主要水文站的径流和水位进行了趋势分析和突变检验， 并从气候变化和人类活动两方面分析其造成洪水危险性增大的原因[19]。本文以湘江流域降雨和径流资料为研究对象，分别将滑动样本熵（Moving Sample Entropy，简称为MSampEn）和滑动移除样本熵（Moving Cut Data Sample Entropy，简称为MCSampEn）应用到降雨和径流时间序列的突变检验中，分析降雨和径流时间序列的复杂性，揭示降雨和径流时间序列的动力学特征。

1研究方法

1.1样本熵

样本熵是Richman等提出的一种新的时间序列复杂性测度方法，有别于近似熵不计入自身匹配的统计量，是对近似熵的改进。它是条件概率严格的自然对数，可以用SampEn（m，r，N）来表示。N为样本时间序列长度；m为维数，一般取2；r为相似容限，一般取（0.1～0.25）D，D为时间序列标准差。样本熵表示非线性动力学系统产生新模式概率的大小，主要用来定量刻画系统的规则度及复杂度。样本熵值越低，时间序列自我相似性越高，产生新模式的概率越低，时间序列越简单；反之，样本熵值越高，时间序列自我相似性越低，产生新模式的概率越高，时间序列越复杂。对于长度为N的时间序列x（i），i=1，2，…，n，其算法如下：

（1）将时间序列按照序号组成一组m维矢量X（i）=（x（i），x（i+1），…，x（i+m-1）），i=1，2，…，N-m+1。

（2）定义X（i）与X（j）间的距离d（X（i）， X（j））为两者对应元素中差值最大的一个，即

d（X（i），X（j））=max（|X（i+k）-X（j+k）|）

k=0，1，2，…，m-1（1）

对于每一个i 值计算X（i）与其余矢量X（j）（j=1，2，…，N-m+1，且 j≠i）之间的d（X（i），X（j）） 。

（3）给定r，对每一个i值统计d（X （i），X（j））

Cmi（r）=k/（N-m）i=1，2，…，N-m+1（2）

（4）对Cmi（r）求平均值Cm（r），即

Cm（r）=∑Cmi（r）/（N-m+1）

i=1，2，…，N-m+1（3）

（5）把维数加1，变成m+1，重复步骤（1）～（4），得到Cm+1（r）。

（6）所求的样本熵为

SampEn（m，r，N）=-ln[Cm+1（r）/Cm（r）]（4）

1.2滑动移除样本熵

滑动移除样本熵是在样本熵的基础上通过滑动移除技术形成的一种突变检测方法。其具体计算过程为：①选择滑动移除数据的窗口尺度S；②从待分析时间序列的第i个数据开始连续移除S个数据，再将剩余N-S个数据直接连在一起得到一个新的时间序列，其中i=1，2，…，N-S+1；③利用样本熵计算新时间序列的样本熵值；④保持移除数据的窗口尺度不变，以步长L逐步移动窗口，重复第②、③步操作，直到原时间序列结束为止；⑤通过第①～④步操作可得到一个随着窗口移动的样本熵时间序列；⑥基于不同动力学性质的数据复杂性不同，而具有相同动力学性质的数据复杂性差异不大的特点，结合第⑤步得到的样本熵时间序列判断突变点或突变区间。

2研究区概况

湘江是湖南省最长、流量最大、流域面积最广的河流，流经湖南省永州、衡阳、株洲、湘潭、长沙等市区，在湘阴县濠河口分两支注入洞庭湖，为洞庭湖水系最大支流。其多年平均流入洞庭湖流量占所有河流多年平均入洞庭湖总流量的22.4%，流量变化对洞庭湖蓄水有着重要影响。其干流全长856 km，流域面积为94 660 km2，在湖南省境内流域面积为85 383 km2。湘江流域属亚热带季风湿润气候，河流水量大多来自降雨，多年平均降水量约为1 436 mm，河流流量受降雨影响很大；由于受季风气候和地貌条件影响，该流域呈现出河川径流年际和年内变化较大、地区分布不均匀以及气候类型多样等特点。

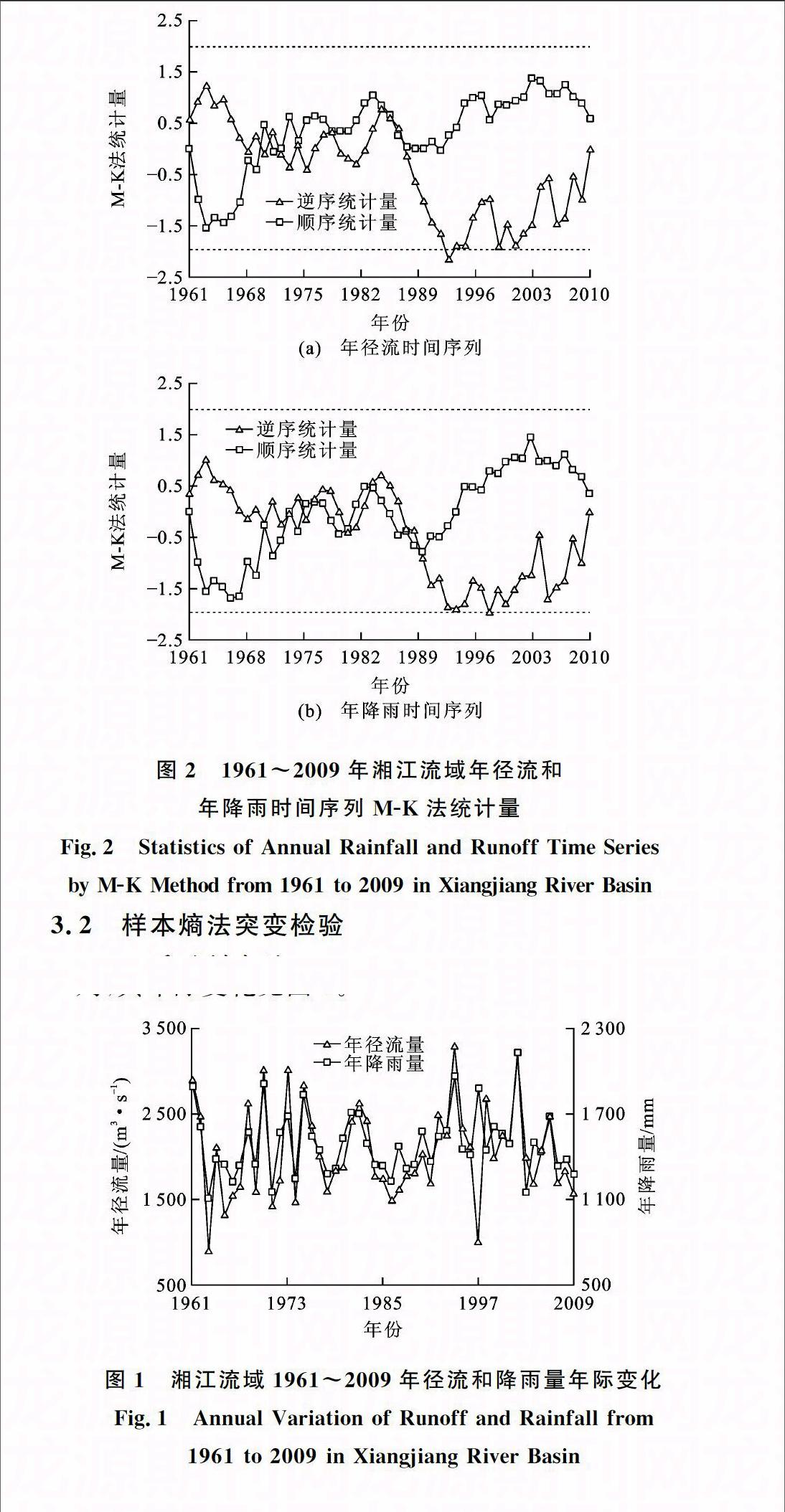
本文采用湘江下游控制站湘潭站1961～2009年逐日径流资料以及流域内道县、永州、常宁、郴州、衡阳、南岳、双峰、株洲等气象站点1961～2009年逐日降雨资料；径流数据来源于湖南省水文水资源勘测局和2001～2011年《长江泥沙公报》；气象数据来自于中国气象科学数据共享服务网（http：∥cdc.nmic.cn/）；运用泰森多边形法计算面平均雨量，构成湘江流域1961～2009年逐日面平均雨量时间序列，其年际变化见图1。

图1湘江流域1961～2009年径流和降雨量年际变化

Fig.1Annual Variation of Runoff and Rainfall from 1961 to 2009 in Xiangjiang River Basin

3结果分析

3.1MK法突变检验

利用传统的突变检验方法MK法对湘潭站1961～2009年年径流和湘江流域1961～2009年年降雨时间序列进行突变检验（图2）。从图2可以看出，年降雨和年径流时间序列的MK法检验结果均未超过95%的显著性水平，呈现不显著的增加趋势。年径流时间序列MK法统计量[图2（a）]在20世纪70年代初有多次交点，在1978年和1985年也有2次交点；年降雨时间序列MK法统计量[图2（b）]在20世纪70年代也有多次交点，在1980年和1989年也有2次交点。MK法统计量表明降雨和径流在20世纪70年代发生多次突变，这与实际不符，且并未超过95%的显著水平，突变不显著，有必要采用样本熵法进行进一步验证。

图21961～2009年湘江流域年径流和年降雨时间序列MK法统计量

Fig.2Statistics of Annual Rainfall and Runoff Time Series

by MK Method from 1961 to 2009 in Xiangjiang River Basin

3.2样本熵法突变检验

3.2.1滑动样本熵

图3不同滑动尺度的降雨和径流时间序列滑动样本熵

Fig.3Moving Sample Entropy of Rainfall and Runoff Time Series in Different Moving Scales

结合滑动技术分别对湘潭站1961～2009年逐日降雨和径流进行样本熵计算，滑动窗口尺度S分别取365、730、1 095、1 460 d，滑动步长L为1 d。随着滑动窗口尺度的增大，得到的样本熵值时间序列越稳定，越易观察样本时间序列的动力学特征。由于不同动力学性质的数据复杂性不同，所以在时间序列点出现明显波动处可能发生突变。图3展示了滑动窗口尺度S为730、1 460 d的滑动样本熵计算结果。从图3（a）、（b）可以看出：径流时间序列动态样本熵值波动较剧烈，整体呈增加趋势，分别在1981年、1986年和2000年前后出现3次波谷，在1991年前后出现波峰；而降雨时间序列动态样本熵值整体呈减小趋势，波动相对较平稳[图3（c）、（d）]，在1970年和1990年前后出现波谷，在2000年前后出现波峰。

3.2.2滑动移除样本熵

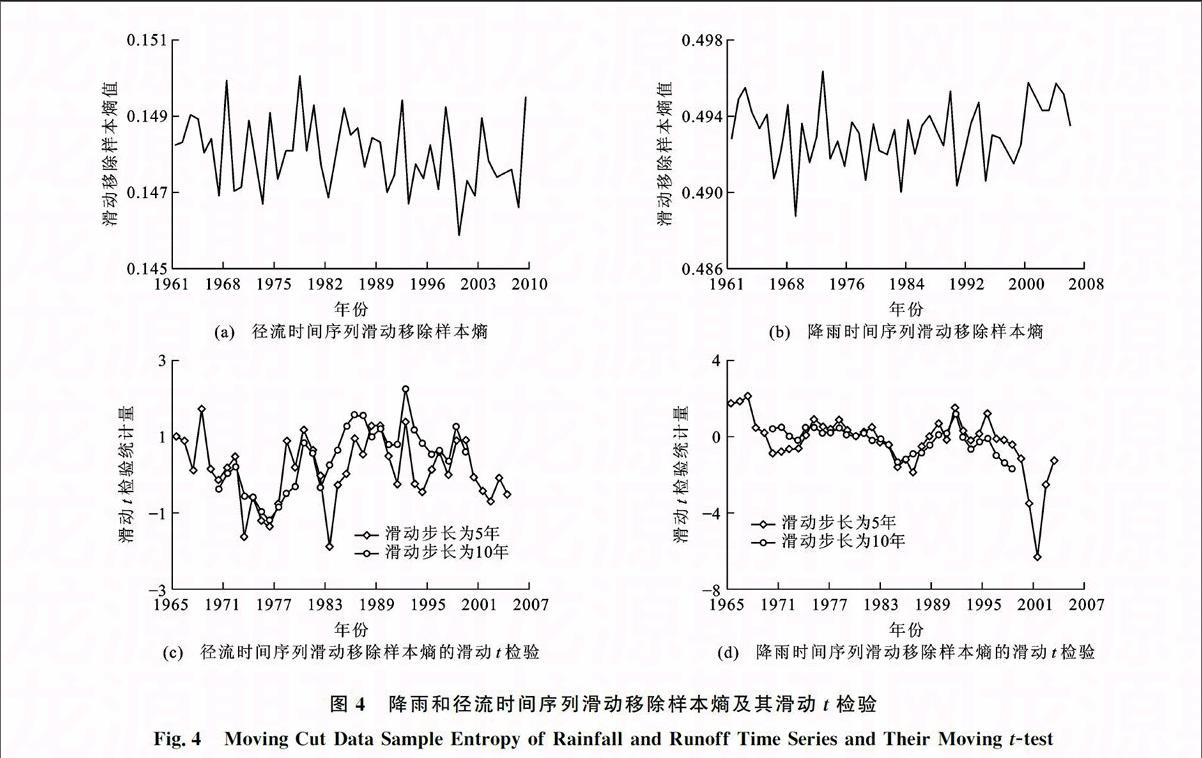
滑动样本熵能够较好地检测样本时间序列的突变，并体现其突变前后的动力学变化特征，但其结果依赖于滑动窗口尺度的大小，并且不能准确定位突变发生的起始点。因此，引进滑动移除技术，将滑动移除窗口尺度S取365 d，滑动步长L取365 d，依次移除1年的数据，将剩余年份的数据直接连在一起得到一个新的时间序列，并计算新生成时间序列的样本熵，得到该移除年份的滑动移除样本熵。对比各年份的滑动移除样本熵，当移除年份前后的滑动移除样本熵发生明显变化时，表明该年份发生突变[图4（a）、（b）]。采用滑动t检验方法对图4（a）、（b）的滑动移除样本熵时间序列进行突变检验，分别取滑动步长6年和10年，选取显著性水平0.05和0.01，结果见图4（c）、（d）。

由图4（c）可以看出：径流时间序列在1966年、1983年、1992年以及2002年发生多次显著突变，且1966年、1992年以及2002年分别通过置信度为95%的置信检验，1983年通过置信度为99%的置信检验；而降雨序列则是在1966年、1987年以及2002年发生3次显著突变[图4（d）]，其中1966年和1987年通过置信度为95%的置信检验，2002年通过置信度为99%的置信检验。

4讨论

由滑动移除样本熵检测到降雨和径流均在1966年发生突变，两者在时间上较一致，这是由于在20世纪50年代初期，河川径流基本处于天然状态，径流主要受到气候变化的影响，所以降雨的突变直接导致径流的突变，并且径流时间序列的复杂度随着降雨时间序列复杂度的增大而增大。径流在1983年发生突变，与径流滑动样本熵时间序列[图3（b）]的第1次波谷相对应，相对的降雨滑动样本熵时间序列[图3（d）]并无明显变化，且该时间与湘江干流第1座水电站湘江水电站的建成时间吻合，表明此次突变与降雨无关，而是受到水利工程的影响。降雨时间序列在1987年发生第2次突变，

图4降雨和径流时间序列滑动移除样本熵及其滑动t检验

Fig.4Moving Cut Data Sample Entropy of Rainfall and Runoff Time Series and Their Moving ttest

与降雨时间序列滑动样本熵的第2次波谷（1990年左右）相对应，而在第1次波谷处（1970年左右）未检测到突变，表明1987年气象条件发生变化，但未引起降雨的突变；径流时间序列滑动样本熵在1987年左右出现第2次波谷，但径流时间序列滑动移除样本熵并未检测到突变，表明降雨的第2次突变造成径流的复杂度发生变化，且在20世纪90年代初，湘江干流第2座水电站宋家洲水电站开始修建，共同导致了径流在1992年发生突变。总之，人类活动的影响导致径流时间序列的复杂度增加。

降雨和径流均在2002年发生突变，但降雨时间序列在突变后复杂度呈减小趋势，而径流时间序列复杂度呈增大趋势。近年来，随着社会经济快速发展，城市化进程不断加快，人类活动明显增强，导致径流时间序列的复杂度不断增大。由中国科学院地理科学与资源研究所完成的1∶100 000土地利用/覆盖数据可以看出，1986～2005年湘江流域的平原旱地减少271.4 km2，城镇用地面积增加661.7 km2，增加量占1986年此类土地利用类型的35%左右[13]，改变了流域的产流条件，且随着水利工程的兴建，人类活动对径流的影响不断增强，相应的气象条件变化对径流的影响相对减弱。

5结语

（1）以样本熵为基础，分别与滑动方法和滑动移除方法相结合，分析了湘江流域降雨和径流时间序列的复杂度变化，并进行突变检验。基于非线性理论的样本熵能够较好地识别水文非线性系统动态演变特征。研究结果克服了传统的突变检验方法MannKendall法不能有效识别非线性时间序列特征，检测突变能力不足的缺陷。

（2）滑动移除样本熵检测到湘江流域径流在1966年、1983年、1992年以及2002年发生多次突变，降雨在1966年、1987年以及2002年发生突变。结合滑动样本熵和滑动移除样本熵的结果发现：径流时间序列在突变后复杂度呈增加趋势，降雨时间序列在突变后呈减小趋势；在人类活动影响较小时，径流时间序列复杂度随着降雨时间序列复杂度增大而增大，而随着人类活动对径流的影响不断增大，径流时间序列复杂度不断增大。

参考文献：

References：

[1]宋晓猛，张建云，占车生，等.气候变化和人类活动对水文循环影响研究进展[J].水利学报，2013，44（7）：779790.

SONG Xiaomeng，ZHANG Jianyun，ZHAN Chesheng，et al.Review for Impacts of Climate Change and Human Activities on Water Cycle[J].Journal of Hydraulic Engineering，2013，44（7）：779790.

[2]孙永东，黄强，王义民，等.滑动近似熵在径流序列突变性分析中的应用[J].水力发电学报，2014，33（4）：16.

SUN Yongdong，HUANG Qiang，WANG Yimin，et al.Application of Moving Approximate Entropy to Mutation Analysis of Runoff Time Series[J].Journal of Hydroelectric Engineering，2014，33（4）：16.

[3]白乐，李怀恩，何宏谋.窟野河径流变化检测及归因研究[J].水利发电学报，2015，34（2）：1522.

BAI Le，LI Huaien，HE Hongmou.Analysis on Detection and Attribution of Runoff Change in Kuye River Basin[J].Journal of Hydroelectric Engineering，2015，34（2）：1522.

[4]周念清，杨硕，沈新平，等.洞庭湖流域降雨序列突变性和多尺度特征分析[J].同济大学学报：自然科学版，2014，42（6）：867872.

ZHOU Nianqing，YANG Shuo，SHEN Xinping，et al.Mutation and Multiscale Characteristics Analysis of Rainfall Series in Dongting Lake Watershed[J].Journal of Tongji University：Natural Science，2014，42（6）：867872.

[5]王国庆，张建云，李雪梅，等.黄土高原昕水河流域径流变化及其对环境要素的响应[J].水土保持研究，2014，21（3）：192196.

WANG Guoqing，ZHANG Jianyun，LI Xuemei，et al.Runoff Variation of the Xinshuihe River Catchment and Its Response to Environment Change on the Loess Plateau[J].Research of Soil and Water Conservation，2014，21（3）：192196.

[6]PINCUS S M.Approximate Entropy as a Measure of System Complexity [J].PNAS，1991，88（6）：22972301.

[7]HORNERO R，ABOY M，ABASOLO D，et al.Interpretation of Approximate Entropy： Analysis of Intracranial Pressure Approximate Entropy During Acute Intracranial Hypertension[J].IEEE Transactions on Biomedical Engineering，2005，52（10）：16711680.

[8]黄宁波，王义民，苏保林.汉江上游洪水特性复杂度分析[J].南水北调与水利科技，2012，10（1）：4548.

HUANG Ningbo，WANG Yimin，SU Baolin.Complexity Analysis of Flood Characteristics in the Upper Hanjiang River[J].Southtonorth Water Diversion and Water Science and Technology，2012，10（1）：4548.

[9]王启光，张增平.近似熵检测气候突变的研究[J].物理学报，2008，57（3）：19761980.

WANG Qiguang，ZHANG Zengping.The Research of Detecting Abrupt Climate Change with Approximate Entropy[J].Acta Physica Sinica，2008，57（3）：19761980.

[10]张亮亮，贾元华，牛忠海，等.基于近似熵的交通流序列趋势变化检测[J].北京交通大学学报，2014，38（6）：711.

ZHANG Liangliang，JIA Yuanhua，NIU Zhonghai，et al.Trend Change Detection of Traffic Flow Based on Approximate Entropy[J].Journal of Beijing Jiaotong University，2014，38（6）：711.

[11]RICHMAN J S，MOORMAN J R.Physiological Timeseries Analysis Using Approximate Entropy and Sample Entropy[J].American Journal of Physiology，Heart and Circulatory Physiology，2000，278（6）：H2039H2049.

[12]彭涛，陈晓宏，庄承彬.基于样本熵的东江月径流序列复杂性分析[J].生态环境学报，2009，18（4）：13791382.

PENG Tao，CHEN Xiaohong，ZHUANG Chengbin.Analysis on Complexity of Monthly Runoff Series Based on Sample Entropy in the Dongjiang River[J].Ecology and Environmental Sciences，2009，18（4）：13791382.

[13]黄生志，黄强，王义民，等.基于启发式分割和近似熵法的径流序列变异诊断[J].中山大学学报：自然科学版，2014，53（4）：154160.

HUANG Shengzhi，HUANG Qiang，WANG Yimin，et al.The Study on the Runoff Change Based on the Heuristic Segmentation Algorithm and Approximate Entropy[J].Acta Scientiarum Naturalium Universitatis Sunyatseni，2014，53（4）：154160.

[14]原继东，王志海.时间序列的表示与分类算法综述[J].计算机科学，2015，42（3）：17.

YUAN Jidong，WANG Zhihai.Review of Time Series Representation and Classification Technique[J].Computer Science，2015，42（3）：17.

[15]CHOU C M.Complexity Analysis of Rainfall and Runoff Time Series Based on Sample Entropy in Different Temporal Scales[J].Stochastic Environmental Research and Risk Assessment，2014，28（6）：14011408.

[16]ZHOU Y，ZHANG Q，LI K，et al.Hydrological Effects of Water Reservoirs on Hydrological Processes in the East River（China） Basin：Complexity Evaluations Based on the Multiscale Entropy Analysis[J].Hydrological Processes，2012，26（21）：32533262.

[17]CHOU C M.Applying Multiscale Entropy to the Complexity Analysis of Rainfallrunoff Relationships[J].Entropy，2012，14（5）：945957.

[18]何文平，何涛，成海英，等.基于近似熵的突变检测新方法[J].物理学报，2011，60（4）：820828.

HE Wenping，HE Tao，CHENG Haiying，et al.A New Method to Detect Abrupt Change Based on Approximate Entropy[J].Acta Physica Sinica，2011，60（4）：820828.

[19]杜鹃，徐伟，赵智国，等.湘江流域近30年径流量与水位的长期变化规律研究[J].应用基础与工程科学学报，2010，18（3）：369378.

DU Juan，XU Wei，ZHAO Zhiguo，et al.Trends of Runoff and Water Level over the Past Thirty Years in Xiang River Basin[J].Journal of Basic Science and Engineering，2010，18（3）：369378.