频繁模式挖掘中基于CFP的应用模型
陈冬玲,曾 文
(1.沈阳大学 信息科学与工程学院,辽宁 沈阳 110044;2.中国科学技术信息研究所,北京 100038)
频繁模式挖掘中基于CFP的应用模型
陈冬玲1,曾 文2
(1.沈阳大学 信息科学与工程学院,辽宁 沈阳 110044;2.中国科学技术信息研究所,北京 100038)
为进一步提高频繁模式挖掘效率,对CFP构造算法做了部分改进,并提出了一些基于此结构的应用方法.实验和分析表明,改进的CFP算法在各种不同的数据挖掘应用中更加有效.
频繁模式;挖掘算法;应用方法;CFP
频繁模式挖掘是目前一个重要的研究领域,并得到了广泛的应用.目前频繁模式的挖掘主要有两类算法.一类是基于Apriori的广度优先算法[1].这种方法的思想是如果一个模式不是频繁模式,那么包含此模式的超模式也一定不是频繁模式.采用循环的方式,通过长度为L-1的频繁模式,组合成长度为L的候选模式,然后扫描数据库得到长度为L的频繁模式.这类方法的思想简单,也不需要复杂的数据结构,容易实现.但这种generation-and-test的方法需要产生大量的候选集,而且需要多次的扫描数据库,这个过程需要花费大量的时间.另一类是基于FP-growth的深度优先算法[2-4],这种算法采用一种新颖的、紧凑的数据结构来存储数据库中所有的频繁项.因为频繁模式中的所有项必须是频繁项,所以挖掘过程不需要在整个数据库中进行.即先扫描数据库,得到所有的频繁项,把所有的频繁项按照一定的顺序插入到频繁模式树中(FP-tree).和Apriori相比,此算法不需要多次重复扫描数据库,前缀结构也可以共享大量的节点.但这种方法结构复杂,FP-tree也只能存储在内存中,挖掘过程还将不断的在内存中产生条件模式树,所以数据集过大时,FP-growth算法需要的空间将超过内存空间.因此这种仅能在内存中进行的挖掘方法只能直接应用于相对较小的数据集.
这两类方法都是耗时耗空间的过程,每个用户对挖掘结果也有不同的要求,如果每次都对整个数据集进行扫描,消耗是巨大的.文献[5-6]提出了一种基于硬盘的数据结构CFP(Condense Frequent Pattern Tree)树来存储从数据集中提取出来的频繁闭模式[7],以后需要此数据集的某些信息只需要访问CFP树,而不需要再次扫描整个数据集.文中对CFP树构造算法提出一些改进,并应用此CFP结构来解决一些实际挖掘问题,实验表明效果是显著的.
1 CFP树
1.1 CFP树的结构
CFP树存储的是整个数据库的频繁闭模式,这样避免了存储大量重复的模式.例如,{c:3,cp:3,cm:3,ca:3,cmp:3,cpa:3,cma:3,camp:3}这些模式可以由一个单一的频繁闭模式cpma:3代替.一个模式X是频繁闭模式就是不存在一个X的超模式X′,使X⊂X′且Support(X)=Support(X′).这样的情况在现实数据集中是常见的.图1a为数据集,图1b、图1c分别是此数据集的频繁模式和频繁闭模式,图1d则是相应的频繁模式树.
如图1d所示,每个CFP树中每一个节点都表示成一个可变长度的数组(root节点除外),数组中的每一项都可以当作一个子树入口,一个节点中的所有项根据它们的支持度按升序排列.此树中的每一条完整路径都代表一个频繁闭模式,同一节点指向的子树都有相同的前缀.对于某个节点中的入口E,假设从根到入口E代表的模式是p,那么入口E存储如下四个方面的信息:①p中的最后一个项;②p的支持计数;③一个指向以p为前缀的子CFP树根节点的指针;④一个hash表,用来表示指针指向的CFP树中所有存在的项.对于每一个入口E,E.item表示储存在E中的项,E.support表示其支持计数,E.child表示指向子CFP树根节点的指针,E.hashtable表示其hash表(root节点没有在图中画出来,它只是一个入口,和一个入口项对应的hash表,并没有任何项的信息).

图1 CFP树Fig.1 CFP-tree
1.2 CFP树的性质
CFP树之所以是紧凑的,并不仅仅是因为它只存储频繁闭模式,而是不同模式的相同前缀可以存储在一条路径中.这一点可以节省大量的空间,而不必分开存储所有的频繁模式.另外CFP树还有如下重要性质可以为将来的运用提供方便[5-6].
(1) Apriori性质.对于CFP树中节点的每一个入口E,由E指向的子树中所有模式的支持计数都不可能大于E.support.可以利用这一性质来简化查询过程,如果入口的支持计数不满足用户定义的最小支持界限,那么就不需要继续查询E所指向的子CFP树.
(2) 左保留性质.从CFP树的结构可以看出,每一个节点中的项按频繁计数升序排列,同时每一个入口所指向的子CFP树中的项都是频繁计数更高的项,即对于入口E,E.item只可能出现在E以前的入口所指向的子树或E自身中.也就是说,如果要找到一个包含E.item的模式,只需要查找E以前的入口和E自己所指向的子树.
(3) 提前返回性质.因为CFP树节点的每一个入口E都有一个hash表,表中记录了E指向的子CFP树包含的所有项.也就是说对一个入口E,如果其指向的子树中包含项i,那么hash表的第j个位置将设为1,j=imodN,N是此hash表的长度.有此结构,在访问子树前,先通过检查hash表来判断要查找模式的所有项是否在子树中,如果在,访问继续进行,否则,查询过程提前终止.这样,查询过程不需要每次访问所有的节点.在这里,hash表的大小是根据CFP树的大小和查询时间来平衡设定的.
1.3 CFP树的构造
CFP树的一个重要性质是它的每一条完整路径都是一个频繁闭模式,这样大大节省了存储空间,所以在树的构造过程中如何移除重复模式是一个重要问题.文献[5-6]中提出了有效的CFP构造算法,但并没有在树的构造过程中移除重复模式,而是在挖掘过程中进行的.本文基于文献[8-9]的研究,提出了对CFP算法的一些改进.
已知一个事务数据库D和一个最小支持阈值,系统需要扫描两次数据库来构造CFP树.首先扫描一次数据库得到所有的频繁项集,并根据它们的频繁计数按升序排列.例如,系统得到频繁项集F={i1,i2,…,im}.i1,i2,…,im按其频繁计数升序排列.然后第二次扫描数据库,对每一个ij∈F,构造条件数据库Dij.在第二次扫描的过程中,删除每一个事务t中的不频繁项并使t中保留的项按F中的顺序排列.如果此时事务t中的第一个项是ij,就把t放到条件数据库Dij中.这样条件数据库就包含所要挖掘的全部信息,系统不需要再次访问原始数据库.
首先挖掘Di1得到所有包含i1的频繁模式,挖掘条件数据库跟挖掘原始数据库采用一样的方式,这是一个递归的过程,当在Di1上的挖掘过程结束后,Di1可以立即被抛弃.虽然它还可能包含其他的项,但这些项都会在挖掘结束后插入到别的条件数据库中,所以抛弃Di1并不会丢失任何挖掘信息.如对Di1中的事务t,此事务中i1的下一个项是ij,那么t=t-i1,然后把t插入到条件数据库Dij中,显然对i1挖掘以后,t别入到Di1以后的条件数据库中.随着j的增大,条件数据库Dij中的事务将越来越多,但每条事务的长度会变短.这一插入过程叫做PushRemain[5-6].
CFP树最重要的特征是它只存储频繁闭模式,下面将讨论如何在树的构造过程中移除重复模式.根据CFP树的特点,考虑一节点N,如果要在这个节点中插入i,假设从根节点到N所代表的模式为p,插入i后得到模式p∩i:sup(i).
考虑节点N的一个入口E所有指向的子树包含i,而且支持度也为sup(i),此时存在模式p∩E.item∩i:sup(i),显然

(1)
由式(1)可以得到,是否需要在节点N中插入i:sup(i),需要检查N的任何子树中是否包含i,且支持度也为sup(i).考虑CFP节点中有hash表,所以可以在N的每一个入口判断i是否存在于某个子树中,如存在,就向下找到在此模式的支持度,如果(p∩E.item∩i).sup(i)=(p∩i).sup(i),p∩i不可能是频繁闭模式,因此i:sup(i)就不需要插入节点N中,从而达到重复移除的效果.算法伪码如下:
Algorithm 1 CFP-Construct Algorithm
Input:
p是一个频繁模式.
Dp是模式p的条件数据库.
Ep是CFP树中模式p所代表的入口.
min_sup是最小支持度阈值.
Detail:
1) 扫描Dp,得到Dp中所有的频繁项和它们各自的支持度,用F={i1:sup(i1),i2:sup(i2),…,in:sup(in)}表示这些频繁项的排列;
2) 建立一个新节点cnode,Ep.child=cnode,新节点暂时为空;
3) 对于所有的i∈F,把i的信息填入hash表中,即Ep.hashtable[imodN]=1,Dp∪i=∅; 循环结束(end for)
4) 对任一事务t∈Dp, 移除t中的非频繁项,把剩余的项按他们在F中的顺序排列; 假设i是t中的第一项,把t插入到Dp∪i中; 循环结束(end for)
5) 对所有的i:sup(i)∈F, 通过入口Ep所指向子树的根节点rootp,检查i是否存在于根节点rootp所有入口指向的子树中,如果存在,访问子树,判断子树中i的支持度是否等于sup(i),如果等于p∩i不可能是频繁闭模式,继续F中的下一个项; 否则,s=p∩{i},把i插入到rootp中的正确位置;Es=i在rootp中的正确位置; CFP_Construct(s,Ds,Es,min_sup); PushRemain(Ds); ∥把Ds中的事务按第一个元素插入到合适的条件数据库 循环结束(end for)
2 CFP树的应用
这种基于磁盘的频繁闭模式存储结构能为多次数据库查询提供方便,文献[5-6]提出了最小支持度限制的查询和项集限制的查询方法.因为在现实应用中,不同用户需要挖掘到不同的信息,在挖掘过程中插入不同的条件[10],所以需要对同一数据集进行多次不同的挖掘.利用CFP结构,仅仅需要在此紧凑的数据结构中进行挖掘,而不需要访问庞大的原始数据库.而且CFP树的结构特点,系统可以更大程度地减少开销.
2.1 带权的频繁闭模式挖掘
CFP是数据集的所有频繁闭模式组成的树结构,由树的构造过程可知,同一个模式不可能出现在两条路径上,所以每次只需要访问一条路径,可见在此结构上提取频繁闭模式非常方便.如访问到某个节点,得到的前缀模式为p:sup(p),那么从其中的一个入口向下访问,下一个项为i:sup(i),如果sup(i) 但通常用户并不是要简单的找到频繁闭模式.如对于一个大型的百货公司,在一个星期内卖出了100块某种香皂,却只卖出了10台某一型号的电冰箱,但这10台电冰箱显然比100块香皂能给商家带来更多的效益.所以在这里要引入一个权值(weight)的概念,权值通常用来衡量对象的重要程度.因此,带权的模式挖掘有很多重要的作用,如上所述的商品利益也是挖掘的重要因素.带权的模式挖掘还可以用来异常检测,医疗诊断等. 文献[11]中提出利用FP-tree进行带权限制的无损频繁闭模式挖掘,在这里将研究在CFP结构中进行此挖掘的算法,CFP结构储存的信息量不仅远小于由原始构造的FP-tree,而且由于它自身的构造特点,可以有效的节省挖掘消费. 一般的频繁模式挖掘都具有Apriori性质,但带权的频繁闭模式挖掘则不能应用此性质,如对于图1所示的数据集,假设每个项都有一个权值Weigths(F)={c:0.70,d:0.60,p:0.60,f:0.65,m:0.50,a:0.90}(冒号后面的小数代表权值),定义一个模式p的权值计算方法为 (2) 定义最小权值限制为2,对于模式cmp:3和cmpa:3,weigth(cmp)=1.800,weight(cmpa)=2.025,显然模式cmp不满足条件,而cmpa满足,显然不能应用Apriori性质通过一个模式不满足条件而放弃检查超模式.在此挖掘过程中,有权值和闭模式两种限制,文献[11]中已证明,这两种限制要按照固定的顺序插入到挖掘过程中,即先判断权值条件是否满足,然后判断是否为闭模式,否则会造成信息丢失.挖掘算法WC_FPMining算法如下: Algorithm 2 WC_FPMining Algorithm Input: P是一个频繁模式 cnode是p指向的CFP树节点 min_sup为最小支持度阈值 min_wei是最小权值阈值 算法: 1) 如果p≠∅,weigth(p)≥min_sup,此时p满足权值条件,然后节点p中的hash表中中找出支持度等于sup(p)且权值最大的项i; 2) 计算weigth(p∪i),如果weigth(p∪i)>min_wei,显然还存在满足条件的p的超集,这样不需要输出p,否则p就是一个带权的频繁闭模式; 3) for对于所有的入口E∈cnode, WC_FPMining(p,E.child,min_sup,min_wei); WC_FPMing(p∪E.item,E.child,min_sup,min_wei); End for(循环结束) 2.2 基于CFP树的关联规则挖掘 关联规则的挖掘[12-14]是数据挖掘中的一个基本领域.关联规则的定义如下: 在CFP中进行关联规则挖掘可以采用Apriori方法,逐代产生频繁模式并判断模式之间能否满足可信度要求.在这个过程中可以用到CFP树中的左保留性质,比如要判断A⟹B是否为关联规则,只需要在包含A或B的最后一个入口的左边查找,这样可以更加缩小操作的范围.这样不仅不需要访问庞大的原始数据库,还可以利用CFP树本身的性质提高挖掘效率. 为了检验改进的CFP结构的工作效率及有效性,采用人工数据集,用VC++做平台编写了部分实验代码,在同一数据集上分别用FP-growth挖掘频繁模式和先构造CFP树然后挖掘频繁模式两种方式进行对比. 由于文中提出的CFP结构,其基本框架仍然是深度优先策略,因而对单个实验而言,文中所提出的改进CFP结构的方法对提高数据库的挖掘效率并没有明显的提高.但若对于多次不同的挖掘工作,实验表明:其一,对于适时数据集的挖掘,一旦数据集发生了更新,利用CFP结构中存储的原始数据集信息,可以只操作更新的信息,然后利用相应的策略把更新的信息插入到此动态结构中,不需要操作整个更新的数据集就可以得到此数据集中有用的信息;其二,为分布式数据挖掘提供方便,因为此结构是基于硬盘的动态存储结构,因而可以从每个客户端得到一个存储局部模式的CFP树,通过文件的形式传递给服务器,然后由服务器合成一个全局CFP树.此结构可以有效的处理分布式数据库的更新问题. 文中对CFP结构做了改进,并利用CFP结构解决数据挖掘中的重要问题.实验表明,经改进的CFP结构在应用中会大大提高数据挖掘的效率,它可以利用有限的资源完成需要解决的问题.但此方法并没有考虑CFP树的更新和合成问题,这是在适时数据流和分布式数据挖掘中的两大关键问题[15],在以后研究中,也会考虑加权聚类的挖掘方式[16]与CFP方法的结合. [1] Han J,Dong G,Yin Y.Efficient Mining of Partial Periodic Patterns in Time Series Database[C]∥Proceedings of 15th International Conference on Data Engineering,Sydney,NSW,1999.Washington,DC: IEEE Computer Society,1999:106-115. [2] Han J,Pei J,Yin Y.Mining Frequent Patterns without Candidate Generation[C]∥Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data,2000.New York: ACM,2000:1-12. [3] Xin D,Han J,Yan X,et al.Mining Compressed Frequent-Pattern Sets[C]∥Proceedings of the 31st International Conference on Very Large Data Bases,Trondheim,Norway,2005.VLDB Endowment,2005:709-720. [4] Borgelt C.Keeping Thing Simple: Finding Frequent Item Sets by Recursive Elimination[C]∥Proceedings of the 1st International Workshop on Open Source Data Mining: Frequent Pattern Mining Implementations,Chicago,USA,2005.New York: ACM,2005:66-70. [5] Liu G,Lu H,Lou W,et al.On Computing,Storing and Querying Frequent Patterns[C]∥Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Washington,DC,USA,2003.New York: ACM,2003:607-612. [6] Liu G,Lu H,Yu J X.CFP-Tree: A Compact Disk-Based Structure for Storing and Querying Frequent Itemsets[J].Information Systems,2007,32(2):295-319. [7] Gade K,Wang J,Karypis G..Efficient Closed Pattern Mining in the Presence of Tough Block Constraints[C]∥Proceedings of the 10th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2004.New York: ACM,2004:138-147. [8] Hou J,Li C.A Pattern Growth Method Based on Memory Indexing for Frequent Patterns Mining[C]∥International Conference on Computational Intelligence for Modelling,Control and Automation,2005 and International Conference on Intelligent Agents,Web Technologies and Internet Commerce,Vienna,2005.IEEE: 663-668. [9] Tseng F,Hsu C.Generating Frequent Pattern with the Frequent Pattern List[C]∥Proceedings of the 5th Pacific-Asia Conference on Knowledge Discovery and Data Mining,Hong Kong,China,2001.London: Springer-Verlag,2001:376-386. [10] Chen Y,Hu Y.Constraint-Based Sequential Pattern Mining: The Consideration of Recency and Compactness[J].Decision Support Systems,2006,42(2):1203-1215. [11] Yun U.Mining Lossless Closed Frequent Patterns with Weight Constraints[J].Knowledge-Based Systems,2007,20(1):86-97. [12] Palshikar G K,Kale M S,Apte M M.Association Rules Mining Using Heavy Itemsets[J].Data & Knowledge Engineering,2007,61(1):93-113. [13] Wolff R,Schuster A.Association Rule Mining in Peer-to-Peer Systems[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B: Cybernetics,2004,34(6):2426-2438. [14] Nanopoulos A,Papadopoulos A N.,Manolopoulos Y.Mining Association Rules in Very Large Clustered Domains[J].Information Systems,2007,32(5):649-669. [15] Chuang K,Chen M.Frequent Pattern Discovery with Memory Constraint[C]∥Proceedings of the 14th ACM International Conference on Information and Knowledge Management,2005.New York: ACM,2005:345-346. [16] 原忠虎,李佳,张博.一种加权的系统聚类方法及应用[J].沈阳大学学报:自然科学版,2014,24(3):201-207. (Yuan Zhonghu,Li Jia,Zhang Bo.A Weighted System Clustering Method and its Application[J].Journal of Shenyang University: Natural Science,2014,26(3):201-207.) 【责任编辑: 肖景魁】 Application Model Based on CFP in Mining Frequent Patterns ChenDongling1,ZengWen2 (1.School of Information Engineering,Shenyang University,Shenyang 110044,China; 2.Institute of Scientific and Technical Information of China,Beijing 100038,China) In order to further improve the efficiency of frequent patterns mining,the CFP construction algorithm is improved and some applications on this structure are proposed.The experiments demonstrate that,the improved CFP algorithm can make different applications more effective and efficient. frequent pattern; mining algorithm; application method; CFP 2015-01-09 辽宁省博士启动基金资助项目(20101074); 国家社会科学基金资助项目(14BTQ038); 中国科学技术信息研究所科研项目预研资金资助项目(YY-201416). 陈冬玲(1973-),女,吉林四平人,沈阳大学副教授,博士. 2095-5456(2015)04-0296-06 TP 274 A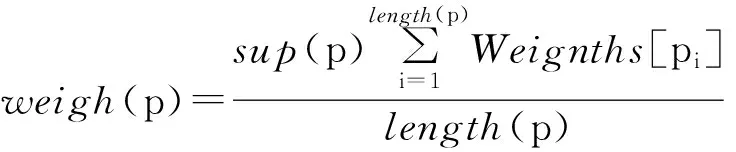
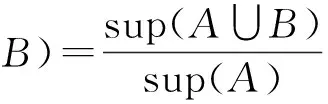
3 实验和分析
4 结 论

