基于全局和局部流形结构的高光谱图像特征提取算法
赵春晖,崔晓辰
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
基于全局和局部流形结构的高光谱图像特征提取算法
赵春晖,崔晓辰
(哈尔滨工程大学 信息与通信工程学院,黑龙江 哈尔滨 150001)
针对目前高光谱图像基于流形学习的无监督特征提取算法中只能够单独描述高维数据空间局部或者全局的几何结构,并且没有一种算法能够同时保持高维数据全局和局部的几何结构的问题,提出了一种基于全局和局部流形结构的无监督特征提取算法(GLMS) 对高光谱图像进行特征提取.算法基于流形学习基本理论,需要建立两种保持流形结构的近邻图,分别用来描述数据的全局和局部的流形结构,通过求解广义特征值问题获得重构权值矩阵进而得到低维嵌入空间的最优投影,以达到降维的目的.在AVIRIS高光谱图像以及Indian Pine和Salina数据集上进行仿真对比实验,结果表明,提出的算法在分类精度和计算效率上有较好的提高.
高光谱图像; 无监督特征提取; 全局和局部流形结构; 流形学习
高光谱图像所具有的大量光谱维为地物信息提取提供了极其丰富的信息[1],有助于更加精细的地物分类和目标识别,然而,光谱维的扩展也会导致数据的冗余和处理数据复杂度的提高.因此,数据降维在高光谱图像处理中起到了十分重要的作用,并且成为高光谱图像分类、混合像元分解、异常目标检测和地物反演等常用到的预处理技术.高光谱图像降维通常包括两种方式:波段选择和特征提取.与特征选择不同的是,特征提取需要对各个光谱波段重新组合和优化,通过数学变换对光谱波段进行压缩,因此,从原始数据集中重建数据往往比直接选择数据应用到后续图像处理会得到更好的效果[2].
近年来,流形学习[3](Manifold Learning)越来越受到学者们的广泛关注,逐渐成为广泛使用的非线性特征提取算法,该理论的基本假设是:高维空间的数据并不是均匀分布的[3],而是嵌入在低维流形上的.Bachmann等首次利用等距特征映射算法(Isomap)[3-4]学习高光谱图像的低维嵌入流形曲面,Isomap算法是一种典型的全局保持流形结构的无监督特征提取算法.局部线性嵌入算法(LLE)[5]考虑到高维数据空间不存在全局的线性结构,但是在样本点的邻域范围内,可以近似地看成符合局部线性欧氏空间.随后提出的拉普拉斯特征映射算法[6](LE)和局部切空间排列算法[7](LTSA)也都是基于局部流形结构这一假设条件.然而,LLE、LE、LTSA这些局部算法并不能给出确定的映射函数,以至于不能将所提的算法应用到新的数据集上,为此,He等对LE算法进行了改进,相继提出了邻域保持嵌入算法[8](NPE)和局部保持投影算法[9](LLP),解决了样本外问题,即能够求解出映射函数.然而上述算法都只能够学习到单一的流形结构,为此,王立志提出了一种线性局部与全局保持的多流行学习算法[10],旨在学习每类数据的几何结构,该方法虽然解决了单一流行结构问题,但需要利用到样本的类别信息,为此本文提出了一种基于全局和局部流形结构的无监督特征提取算法(Global and Local Manifold Structure Feature Extraction Algorithm,GLMS),并且通过引入参数使得求解的重构权值矩阵达到最优.无监督特征提取算法通过构造图嵌入的模型来同时保持不同类别数据的几何结构,包括全局和局部几何结构,求解两种近邻图的重构权值矩阵,最后通过求解广义特征值问题得到最佳投影.
1 基于全局和局部流形结构的特征提取算法
1.1 问题描述
给定一组高光谱数据样本点,首先要建立一个关于样本数据的近邻图.由于需要考虑高维数据的全局和局部的几何结构,因此需要建立两种保持流形结构的重建矩阵.其中一个用来描述局部的流形结构,利用近邻图中相互连接的数据样本点的线性重构权值矩阵;与此同时,另外一个描述全局的流形结构,利用最短路径算法求解成对的数据样本点,因为这些样本点在近邻图上不是相互连接的.最后通过求解广义特征值问题获得最优的嵌入投影函数.这样,不同的局部和全局流形结构才能同时保持于低维的嵌入空间中.
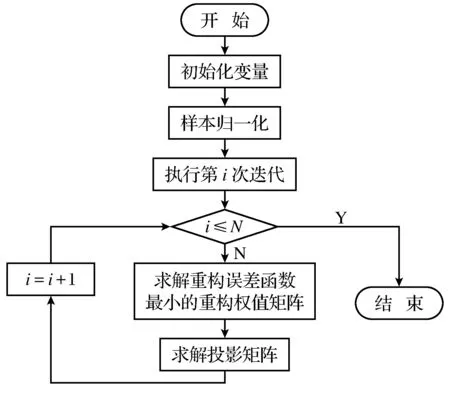
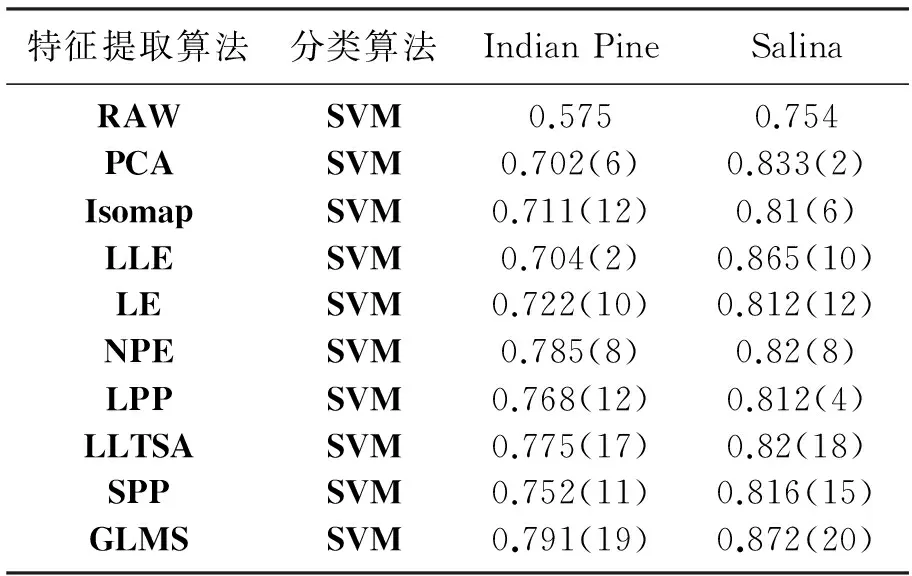
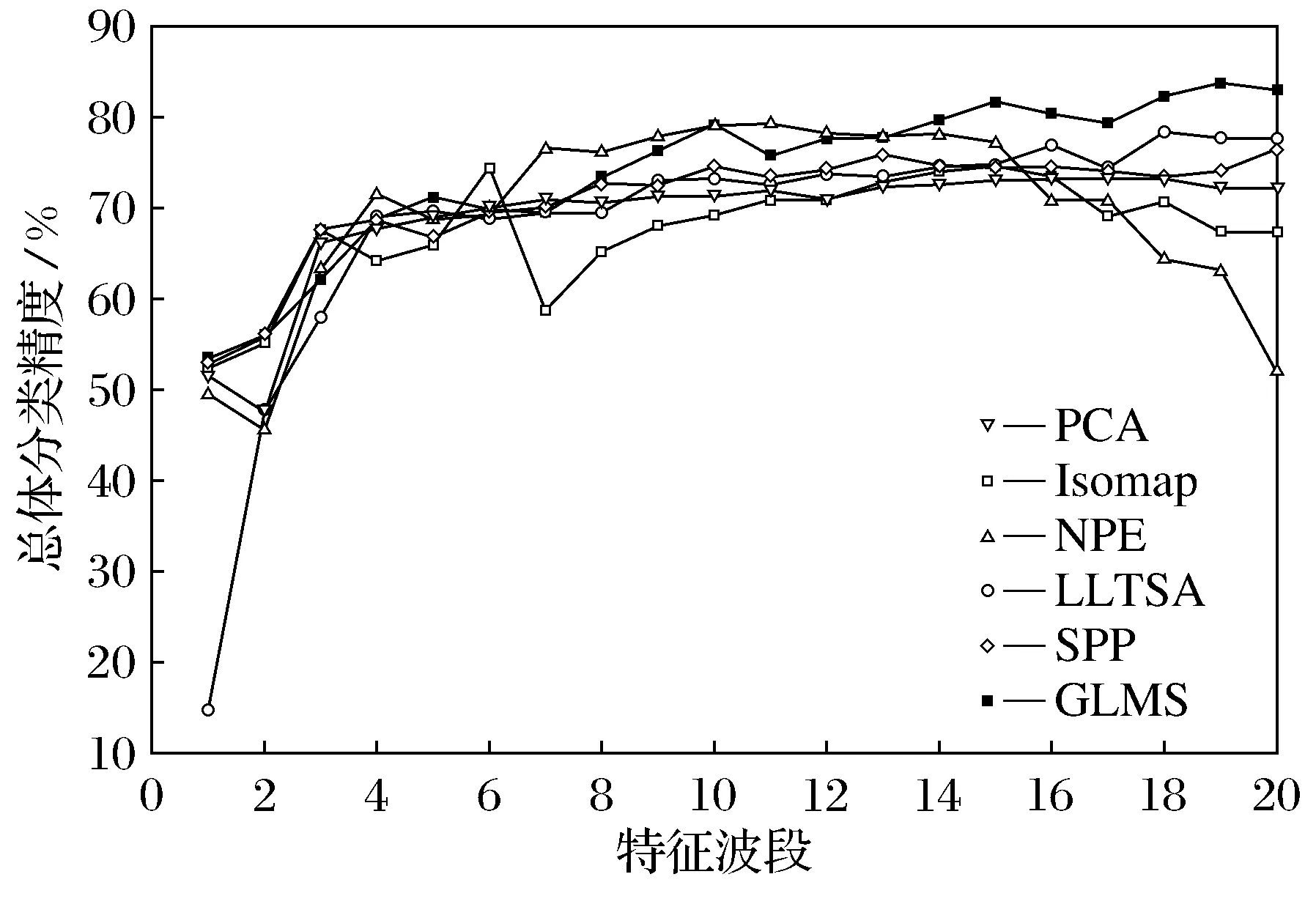
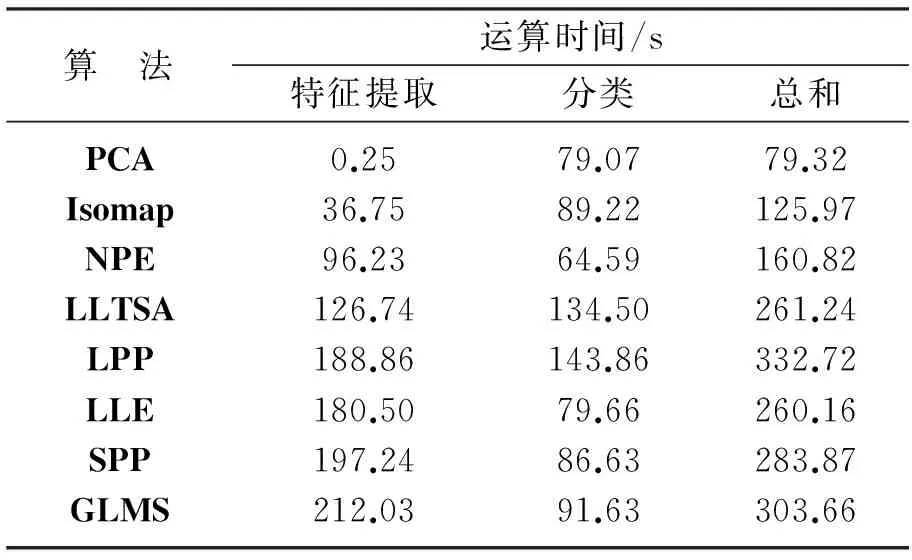
令X={x1,x2,…,xN}(xi)∈(RD)表示高光谱图像数据样本集,Z={z1,z2,…,zN}(zi)∈(Rd)是其低维表示,其中,d (1) 式中,投影矩阵W=[w1,w2,…,wd]∈RD×d. 1.2 保持局部几何结构模型 为了保持局部流形结构[11],首先要建立K近邻图G,其中,从原始数据集中选择m个样本点xi(i=1,2,…,m),若样本点i在样本点j的邻域范围内,则将这两个点连起来构成连接.从某种意义来说,样本点会分布在非线性的嵌入流形结构上,但是可以假设每一个局部的近邻域都是线性的,类似于局部线性嵌入算法中,可以将这些局部的几何结构通过线性的相关矩阵来重建每一个来自其近邻点的样本重构.重构误差函数如下式所示: (2) 式中,NK(xi)表示样本点的K近邻.需要说明的是,式(2)的约束条件是:如果样本点j不在样本点i的K近邻域内,那么可以通过求解最小化问题来得到变换矩阵.在低维嵌入空间中,为了保持局部的流形结构,需要对下式求取最小化: trace(YMYT)=trace(ATXMXTA). (3) 式中,Y=(y1,y2,…,ym),X=(x1,x2,…,xm),M=(I-W)T(I-W),I=diag(1,…,1).可以容易地知道,矩阵M是对称且半正定矩阵.考虑到一维的情况,最优的投影矩阵可以通过求解最小化问题得到解决,如下式所示: (4) 式中,a是n×1的向量. 1.3 保持全局几何结构模型 在保持局部流形结构[7]的同时,还要同时考虑高维数据的全局几何结构.首先建立一个K近邻图G的互补图Gc.在这个互补图Gc中,如果样本点i和j在近邻图G中不是互相连接的,那么就需要将这两个样本点相互连接起来.这样,G+Gc就构成了样本点的完整近邻图.因此可以确定原始数据空间中的全局几何结构,并且通过寻求一种嵌入映射f,可以保持测地线距离在低维嵌入的欧氏空间中,条件是两个样本点在互补图Gc中是互相连接的,如下式所示: (5) 式中,dM(xi,xj)表示流形结构上的两个样本点间的测地线距离,d(f(xi),f(xj))表示在低维嵌入空间中的欧氏距离.在表达真实地物的高光谱图像数据集中,基本的流形结构通常是未知的,因此通过求解样本点间的测地线距离的方法也是未知的.所以只能够通过求解近邻图G上两个样本点间的最短路径dG(xi,xj)来近似地估计出样本点间的测地线距离dM(xi,xj).计算最短路径问题的过程如下:初始化dG(xi,xj)=d(xi,xj),如果样本点i,j是相互连接的,那么dG(xi,xj)=∞;然后对于数据集中的每一个样本点重复上面的操作,通过求解如下最小化问题来代替求解最短路径问题dG(xi,xj): (6) 最终的矩阵DG={dG(xi,xj)}包含在近邻图G的所有样本点的最短路径,如下式所示: (7) 1.4 算法描述 (8) 考虑线性的嵌入映射:f(x)=aTx.令yi=f(xi),Y=aTX,则 (9) 所以,最佳的投影矩阵可以通过求解如下最优化问题得到解决: (10) 式(10)的推导过程如下: trace(aTXXTaaTXXTa). (11) (12) 经过上述推导,最优的投影向量可以表示为 aTXXTaaTXXTa)-λ2aTXMXTa]}. (13) (14) 向量ai可以将式(14)最大化,并且可以转换为求解特征值和特征向量问题,如下式所示: (15) 在实验中,令λ1=常量,即能够求解出在不受全局结构影响下的局部最优重构权值矩阵;令λ2=常量,即能够求解出邻域内每一个样本点都用其邻域内的点线性表示时的全局最优解. 令A=(a1,a2,…,ad),线性映射描述如下式所示: (16) 式中,y为高光谱图像数据的低维表示. 1.5 评价指标 总体的分类精度(Overall Classification Accuracy,OCA)是一个比值,分母代表所有原始的高光谱数据的样本点的数量,分子代表经过分类方法正确分类的数据个数,如下式所示: (17) 2.1 算法步骤描述 输入: 高光谱图像数据样本集X={x1,x2,…,xN}∈RD. 步骤1: 对输入数据进行初始化. 步骤2: 根据式(4)求解出保持局部几何结构的重构权值矩阵. 步骤3: 根据式(7)求解出保持全局几何结构的重构权值矩阵. 步骤4: 根据式(14)求解出同时保持高维数据样本的全局和局部几何结构的投影向量. 步骤5: 计算出重构权值矩阵对应的最大的d个特征值对应的特征向量,构成投影向量A. 步骤6: 求解高维数据的低维嵌入坐标,x→y=ATx. 输出:特征提取算法处理后的低维数据Z={z1,z2,…,zN}∈Rd. 2.2 算法流程图 图1是求解保持局部几何结构的重构权值矩阵的算法流程图. 3.1 实验数据 实验所用计算机搭载64-bits,主频3.5 GHz Intel i7 4770 K CPU,内存16 G,三级缓存8 MB.软件环境:MATLAB 2011b.本文实验采用AVIRIS高光谱遥感图像.Indian Pine数据集取自1992年6月拍摄的美国印第安纳州西北部印第安遥感试验区的一部分,图像大小为145×145像素,共包含220个波段,像素深度为16 bits,波长范围为400~2 500 nm,包含16类确定类别的地物.AVIRIS Salina高光谱数据由AVIRIS成像光谱仪在加利福尼亚地区收集获取,拥有工作波段224个,含有512×217个像素,空间分辨率为4 m,包含16种真实地物类别.图2a为Indian Pine高光谱数据集的灰度图,图2b为Indian Pine高光谱数据集的类别标记图.图3a为Salina高光谱数据集的灰度图,图3b为Salina高光谱数据集的类别标记图. 图1 求解保持局部几何结构的重构权值矩阵的算法流程图Fig.1 The flow chart of reconstruction weight matrix of the local geometric structure 图2 Indian Pine高光谱数据集的灰度图及类别标记图Fig.2 Gray scale map and labeled graph ofhyperspectral data set of Indian Pine 实验的数据样本X为无标签数据样本部分随机地采样于原始的高光谱数据集,其中,70%随机地从原始数据集中选取作为训练样本,剩余的30%作为测试样本.为了调查出训练样本大小对分类性能的影响,初始的训练样本个数的选取也应不同.实验中,分类算法选取支持向量机SVM算法,使用RBF Kernels(径向基核函数).每次实验做10次,取平均值,并且结果利用OCA和Kappa系数来评价特征提取算法的分类性能.选择高斯核函数,其宽为0.02,惩罚是10.基于流形学习的特征提取算法的近邻参数选取不是固定的,在实验中,对式(15)的求解通常是令其中一个参数常量化,即实验中令λ2=1,保证在不受局部特性干扰的情况下求解出全局最优解;并且将本文提出的算法和经典的算法进行了比较.本次实验分别使用PCA,Isomap,LLE,LE,NPE,LPP,LLTSA,SPP,GLMS等算法对性能进行验证. 图3 Salina高光谱数据集的灰度图及类别标记图Fig.3 Gray scale map and labeled graph ofhyperspectral data set of Salina 3.2 实验结果 表1为不同特征提取算法的最高总体分类精度显示.其中,黑体显示的为每一种数据集中不同算法中最高的总体分类精度,括号里表达的是最高总体分类精度对应的降维后的最优波段数. 表1 不同特征提取算法的最高总体分类精度Table1 The highest overall classification accuracy for different feature extraction 由表1可以总结出如下结论. (1) 对于高光谱数据样本集来说,不同的特征提取算法可以提高数据集的分类性能,大多数的信息都将能保留下来以便为后续的分类服务.对于Indian Pine数据集,经过PCA特征提取后的低维子空间经过SVM后的总体分类精度并没有原始数据集的精度高,因此可以推论:由于PCA是线性特征提取算法,其不能提取出原始数据集中由于大气、水分等产生的非线性折射产生的数据间的相关性和非线性因素. (2) 不同的算法在应用到不同的数据集时,得出的总体分类精度也是有差别的.当标签样本的数量有限时,半监督算法相对于其他不考虑正则化参数的算法来说得到的,总体分类精度就要减少许多. (3) 与无监督算法SPP比较,充分利用了高光谱数据少量先验类别信息的算法,获得了更高的总体分类精度.相比于其他基于流形学习的降维算法,由于不用考虑参数的影响,曲线平滑上升.而对参数敏感的流形算法,在一些特定的维数时,总体分类精度会不稳定. (4) 本文提出的算法并不是在所有的波段都表现良好,例如在维数为7~11维时,总体分类精度小于LLTSA算法.在维数大于14时,总体分类精度是所有算法中最高的,原因是考虑到了数据集局部的几何关系,效果好于全局算法.而且由于算法不需要设置额外的参数,因此在总体分类精度这项指标上比SPP算法要稍微弱一点. 图4为Indian Pine高光谱数据集不同算法对应的总体分类精度.由图4可以看出,各算法降维到7波段后,总体分类精度趋于稳定并且达到了最高点,由此得出:降维后的波段数过小,将损失高光谱数据样本的原始信息,然而低维子空间的维数如果选取得过大,又会使得运算复杂度过高,失去了特征提取的意义,况且得到的低维数据与原始数据相比并不能体现出降维的优势.由于考虑了全局和局部的几何结构,因此本文提出的算法在分类精度这一指标上要优于其他保持单一流形结构的特征提取算法. 图4 Indian Pine高光谱数据集不同算法对应的总体分类精度Fig.4 The overall classification accuracy ofdifferent algorithm graph of hyperspectraldata set of Indian Pine 图5为Salina高光谱数据集不同算法对应的分类图.由图5能够直观地看出各种数据源下的通过SVM算法分类后的效果图,能够得出结论:经过GMLS算法降维后的低维数据应用SVM支持向量机分类后得到的分类效果在几种算法中最优,几乎能够识别出全部的不同的地物,而且可以看出其他算法都或多或少地将某些地物错分. 图5 Salina高光谱数据集不同算法对应的分类图Fig.5 The classification map of different algorithmgraph of hyperspectral data set of Salina 表2所示为Indian Pine数据集不同特征提取算法的运算时间.每种算法在相同的条件下,分别运算10次取均值.本文算法的计算复杂度主要包括近邻图搜索和广义特征值求解,与样本个数N和维数D有关,而GLMS算法的计算复杂度主要包括寻找近邻图,计算复杂度为o(DN2).当N≫D时,本文提出的算法虽然比以往传统的算法耗费时间长,但是考虑到GLMS算法同时考虑了高维数据空间的不同几何结构,而且本文提出的算法在后续的数据分类中显示出较高的性能,计算时间也只是比SPP算法多了14.79 s,相比于优点,这些时间几乎可以忽略. 表2 Indian Pine数据集不同特征 提取算法的运算时间Table2 The operation time of different algorithm graph of hyperspectral data set of Indian Pine 考虑到半监督算法需要事先知道原始数据集的先验知识,而无监督算法则不需要,然而,目前基于流形学习的无监督算法只能够单独地描述局部或者全局的几何结构,通过构建两种图来实现不同流形结构的统一.然而正是由于构建近邻图要搜索全局结构和局部结构的图构造策略,造成了在算法复杂度上的提高,因此,算法的改进还要围绕着如何在减少搜索近邻图的时间复杂度上来提高. [1] Plaza A,Benediktsson J A,Boardman J W,et al.Recent Advances in Techniques for Hyperspectral Image Processing[J].Remote Sensing of Environment,2009,113(1):110-122. [2] Green R O,Eastwood M L,Sarture C M,et al.Imaging Spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS)[J].Remote Sensing of Environment,1998,65(3):227-248. [3] Bachmann C M,Ainsworth T L.Bathymetric Retrieval from Manifold Coordinate Representations of Hyperspectral Imagery[C]∥IEEE International Conference on Geoscience & Remote Sensing Symposium.IEEE,2007:1548-1551. [4] Bachmann C M,Ainsworth T L,Gillis D B,et al.Modeling Coastal Waters from Hyperspectral Imagery Using Manifold Coordinates[C]∥IEEE International Conference on Geoscience & Remote Sensing Symposium.IEEE,2006:356-359. [5] Belkin M,Niyogi P.Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering[J].Advances in Neural Information Processing Systems,2002,1(14):585-591. [6] 齐滨.高光谱图像分类及端元提取方法研究[D].哈尔滨:哈尔滨工程大学,2012:13-34. (Qi Bin.Research on Hyperspectral Image Classification and Endmember Extraction Methods[D].Harbin: Harbin Engineering University,2012:13-34.) [7] Zhang T H,Yang J,Zhao D L,et al.Linear Local Tangent Space Alignment and Application to Face Recognition[J].Neurocomputing,2007,70(7):1547-1553. [8] He X F,Cai D,Yan S C,et al.Neighborhood Preserving Embedding[J].IEEE International Conference on Computer Vision,2005,2:1208-1213. [9] He X F,Niyogi P.Locality Preserving Projections[J].Advances in Neural Information Processing Systems,2004,2(16):153-160. [10] 王立志.基于流形学习的高光谱图像降维与分类研究[D].重庆:重庆大学,2012:34-56. (Wang Lizhi.Research on Dimensionality Reduction and Classification of Hyperspectral Image Based on Manifold Learning[D].Chongqing: Chongqing University,2012:34-56.) [11] 甘资先,周方俊,肖奕.多维尺度分析中的算法研究[J].清华大学学报:自然科学版,1991,31(6):20-27. (Gan Zixian,Zhou Fangjun,Xiao Yi.Study on the Algorithm for Multidimensional Scaling[J].Journal of Tsinghua University: Natural Science,1991,31(6):20-27.) 【责任编辑: 李 艳】 Hyperspectral Image Feature Extraction Algorithm Based on Global and Local Manifold Structure ZhaoChunhui,CuiXiaochen (School of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China) High spectrum image manifold learning unsupervised feature extraction algorithm can only separate description based on high dimensional data space whether it is local or global geometric structure or not,there is no algorithm can also maintain a high dimensional data of global and local geometric structure.A novel unsupervised feature extraction algorithm is proposed based on global and local manifold structure (GLMS) for feature extraction of hyperspectral image.Manifold learning algorithms are based on the basic theory,which establishes two maintain manifold structure neighbor graphs,and it is applied to describe the data of the global and local manifold structure,by solving the generalized eigenvalue problem to obtain the optimal projection reconstruction weight matrix and then to get the low dimensional embedding space to achieve the purpose of reducing dimension.In the AVIRIS hyperspectral image tests on Indian Pine and Salina data set,experimental results show that the proposed algorithm has better improvement in classification accuracy and computational efficiency. hyperspectral image; unsupervised feature extraction; global and local manifold; manifold learning 2015-01-15 赵春晖(1965-),男,黑龙江汤原人,哈尔滨工程大学教授,博士生导师. 2095-5456(2015)04-0283-06 TN 911.2 A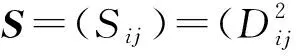
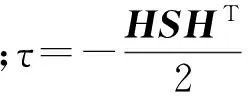
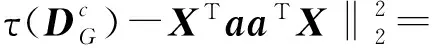
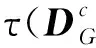

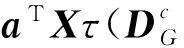

2 算法步骤及流程图
3 实验结果及分析



4 结 语

