不同维GM(1,1)模型在基坑地表沉降预测中应用

郑 丽,白宝玉

(1.宿州学院 环境与测绘工程学院,安徽 宿州 234000; 2.重庆市公安局 科技信息化处,重庆 400000)

不同维GM(1,1)模型在基坑地表沉降预测中应用

郑 丽1,白宝玉2

(1.宿州学院 环境与测绘工程学院,安徽 宿州 234000; 2.重庆市公安局 科技信息化处,重庆 400000)

根据地铁工程施工中基坑地表沉降监测数据,引入灰色系统理论,建立不同维GM(1,1)预测模型,对基坑开挖引起的周边地表沉降作了预测和分析.通过残差和后验差法对模型的可靠性进行检验,通过实证分析了在基坑地表沉降预测中应用灰色模型的可行性.研究结果表明构建不同维灰色模型,随着参与建模的数据维度的增加,发展系数-a逐渐减小,而灰作用量b、后验差指标C及平均相对误差均呈现增大的趋势,所建不同维GM(1,1)模型精度均达到了一级,尤以4维GM(1,1)模型累计沉降量实测值与累计沉降量预测值吻合较好,满足短期预测需求.可见针对基坑周边地表沉降需要的建模数据较少,便于节约长期观测成本,可为工程后继施工提供一定的理论依据.

基坑工程; 不同维GM(1,1); 地表沉降; 预测

随着城市地下空间的开发,基坑工程引发的地表沉降灾害评估成为地面沉降控制与管理、地质灾害防治的重要措施.城市地下工程由于埋置深度浅,基坑开挖和施工降水过程中,土体原来的应力平衡状态受到破坏,导致基坑周围地表产生不均匀沉降[1].地表沉降的产生将对周边建(构)筑物或地下管线带来不同程度的影响,过大的地表沉降还会造成建(构)筑物的破坏,引发经济损失和安全事故.为此,在基坑施工期间必须对基坑周围的环境进行监测.其中,地表沉降观测是其中重要的一个方面.通过定期观测,掌握其沉降变形规律,并通过建立相关模型获得预测变形值,以便及时采取适当的预防或善后措施,确保基坑周边环境的安全.

在城市轨道交通工程建设中,变形监测数据处理与信息反馈是信息化施工和管理的重要组成部分,是保证安全施工、工程环境安全和社会稳定必不可少的有效措施.近年来,关于基坑地表沉降预测的方法大体上分为回归模型、灰色模型、人工神经网络模型,这些预测方法均基于时间序列数据建立预测模型,得出预测结果.灰色模型的本质是指数拟合,当原始序列隐含着指数变化规律时,灰色GM(1,1)模型预测方法是非常成功的[2].它是灰色系统理论的核心内容之一,其以较少的数据进行预测和分析,建模简单,公式简洁,易于求解,具有可检验性等诸多优点,成为预测系统动态分析及控制的基础[3].目前,很多学者就灰色模型在基坑工程预测中展开了研究,如吴杰等[4]考虑了该点位移和围护桩上其他点的位移及锚索拉力是耦合的,采用多因素灰色G(1,N)模型对基坑位移进行预测,取得了较好的预测精度.卢志刚等[5]采用灰色理论GM(2,1)二阶线性动态模型应用于基坑工程中,对基坑的水平位移和沉降预测进行了计算,得到较好精度.陈晓斌等[6]将GM(1,1)和GM(2,1)模型应用到基坑工程中,通过编制计算程序,完成其在锚杆拉力、地面沉降和地面水平位移预测计算,通过实证分析得出GM(1,1)比GM(2,1)模型更可靠、稳定性高.值得注意的是预测中这些对原始数据要求都是等时距的,但是对于在基坑工程预测中选择多少维原始数据参与建模效果并未进行分析.

鉴于此,本文针对某地铁车站施工过程中地表沉降监测的一个监测点连续多期的沉降实测资料进行分析,应用灰色理论进行沉降变形的预测和检验,对监测数据进行分析、处理和建模,并比较了不同维灰色预测模型处理该工程的模型精度,以期为周边地表沉降变形预报工作提供一定的参考.

1 GM(1,1)模型概述

灰色动态预测模型,通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而对系统的时间序列进行数量大小的预测,即对系统的主行为特征量或某项指标,发展变化到未来特定时刻出现的数值进行预测[7].

1.1 模型的建立

对给定的初始变量X有n个原始数据,组成一个非负离散时间序列如下:

(1)

对序列x(0)进行一次累加,生成新数列x(1)={x(1)(1),x(1)(2),….,x(1)(n)},令z(1)为数列x(1)的紧邻均值生成数列,即

其中:k=2,3,…,n;a=0.5.

称方程

(2)

为GM(1,1)模型的基本形式,式中参数-a为发展系数,b为灰作用量.

引入如下矩阵向量记号:

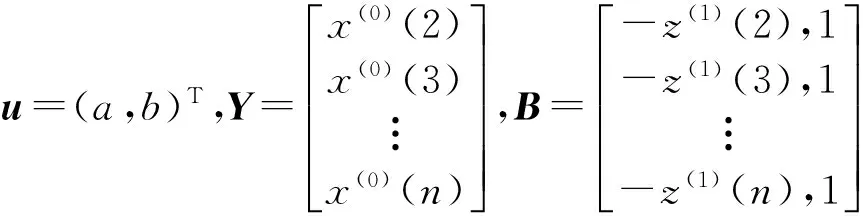
于是GM(1,1)模型中式(2)可表示为Y=Bu采用最小二乘法可求得参数a,b的估计值u=(a,b)T=(BTB)-1BTY.

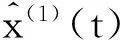
(3)

其被称为GM(1,1)模型的白化方程,也称影子方程,这是一个一阶线性非齐次常微分方程模型.

1.2 模型的求解

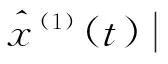
(4)

其中k=1,2,…,n-1,可知式(4)为GM(1,1)预测方程.

从式(4)通过累减还原得到原始数据列x(0)的还原值(预测值)

(5)

其中,k=1,2,…,n-1.

表1 模型的应用范围表Table1 The extent Tableof the application of model

1.3 模型的精度检验

为了分析模型的可靠性,必须对模型进行诊断.目前通用的诊断方法是对模型进行后验差法检验[9].这里定义残差如下:

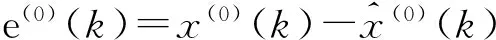
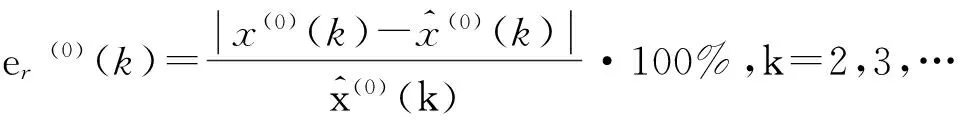
一般认为,当相对残差小于20%时,达到一般要求;当相对误差小于10%时,达到较高要求.

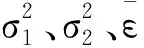
若后验差指标C小,表明即使原始数据离散,模型值与实际值的差并不离散,小误差概率P越大,且为1时最好.

表2 P、C值与预测精度Table2 The value of P,C and prediction accuracy

2 工程实例

2.1 地铁车站工程周边环境及工程地质

拟建场地位于广场内,站址现状为绿地,出入口周边用地规划为绿地用地,站位距离周边建筑物较远,对其使用影响较小,主体结构范围内有电力管线需要采取迁移和保护措施.本站地势平坦,地面吴淞高程一般为16.61～18.75 m,场地地貌类型属阶地,发育有坳沟亚地貌,基坑深度范围的各土层主要为人工填土、软弱土、中硬土及基岩,地下水类型主要为松散地层中的孔隙水、基岩裂隙水.

为确保地铁车站的安全施工及周围环境的稳定,采用精度为二等的光学水准仪对地铁车站基坑工程进行地表沉降监测,表3为某个地表沉降监测点的实测值,监测周期为1 d.表3所列数据为连续14 d观测所得14期数据,通过定期的监测点的沉降变化速率和累积沉降量来判断基坑周围环境的整体稳定性.

根据表3绘制地表沉降监测点变化趋势图,从图1中可以看出:地铁车站基坑周边地表沉降监测点14期实测数据显示最大沉降量为3.7 mm,最小为2.1 mm,累计沉降量高达39.8 mm,平均沉降量2.8 mm/d,地表沉降点略有下沉,但变化速率不大,沉降趋于稳定.

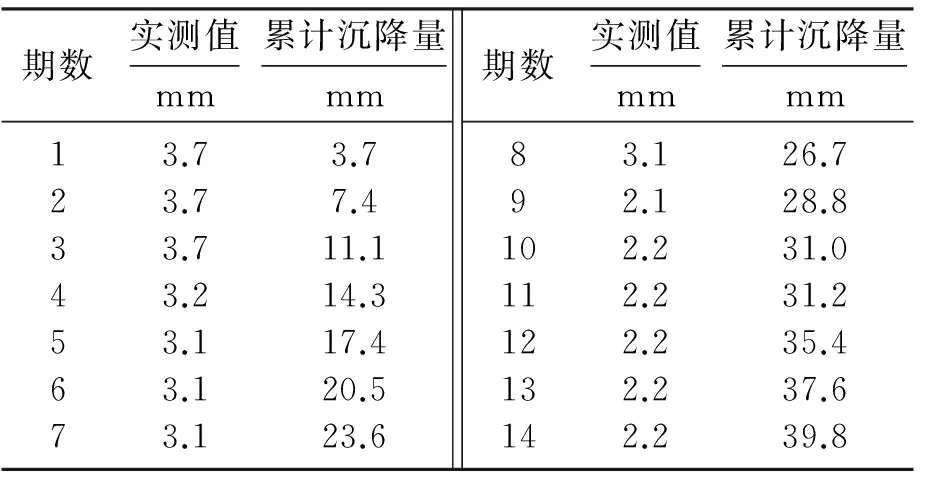
表3 地表沉降监测点实测沉降数据Table3 The actual monitoring data of ground surface settlement on monitoring point

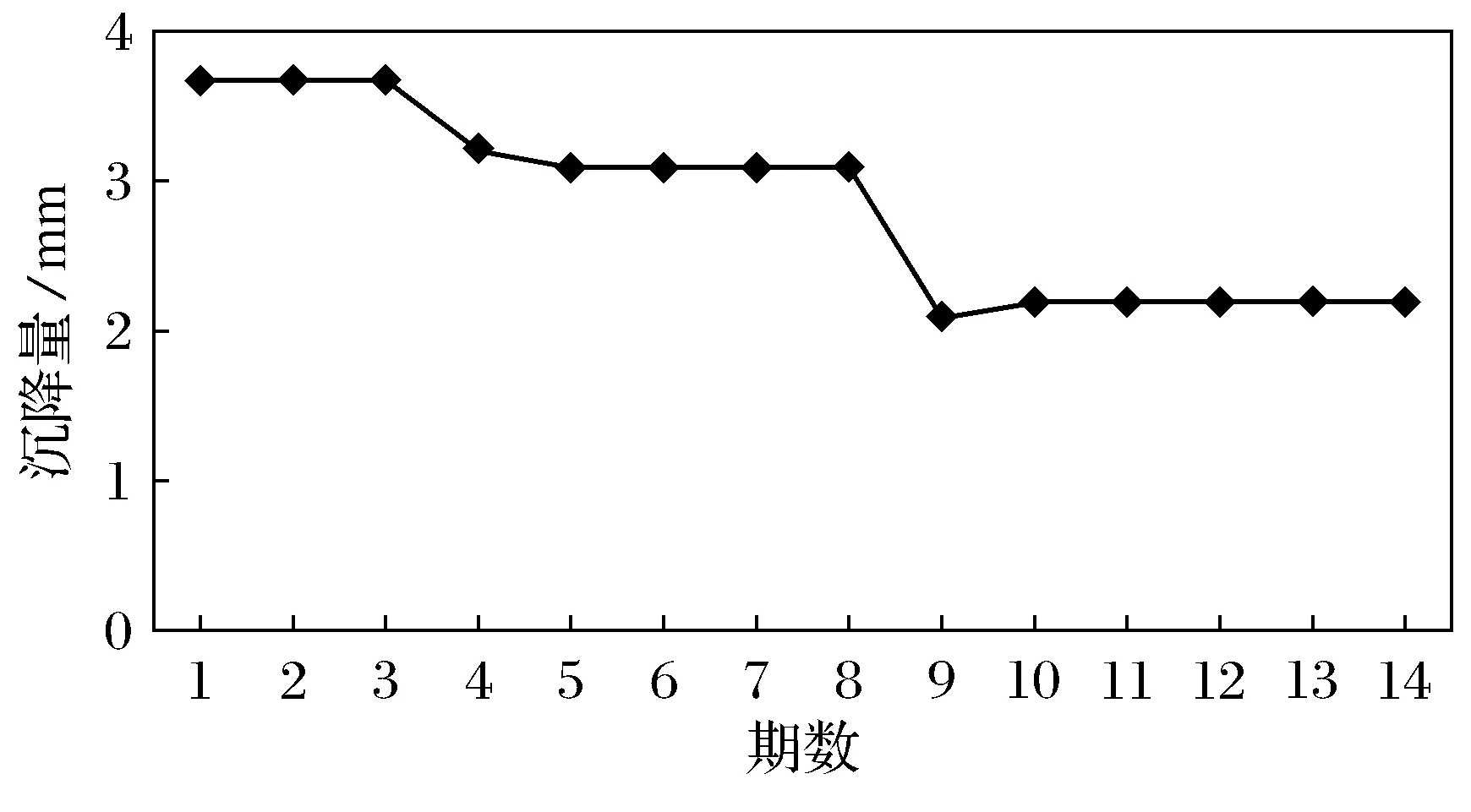
图1 地表沉降监测点实测值变化示意图Fig.1 Diagram of actual monitoring data of groundsurface settlement on monitoring point

2.2 构建不同维GM(1,1)基坑地表沉降预测模型

由于基坑变形是多因素作用的结果,其变形系统的实质是一个灰色系统,故可采用灰色系统理论对其变形进行预测研究[10].依据表3所提供数据作为样本数据,分别构造4～14维的GM(1,1)模型,计算模型参数,GM(1,1)模型得到指定时间段内的预测值,根据实际问题的的需要,对实际沉降量与预测值进行比较.以建立4维GM(1,1)模型为例,阐述建模过程,表中前4个数据构成原始序列x(0)(k)=(3.7,3.7,3.7,3.2),对其进行一次累加生成累计沉降观测值x(1)(k)=(3.7,7.4,11.1,14.3).

表4 地表沉降监测点沉降观测值与预测值Table4 The actual monitoring data and predicted value of ground surface settlement on monitoring point

建立4维GM(1,1)模型为:

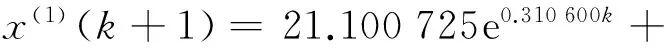
其中,发展系数-a=0.310 600,灰作用量b=5.404 65.

由此根据表1所示可知,当-a>0.3时,所建预测模型适用于短期预测,进一步计算,得出后验差指标C和小误差概率分别为C=0.095 0,P=1.000 0,对照表2可知,预测精度为好,点的累计沉降模型达到一级预测精度.如表4所示,该沉降监测点的累计沉降观测值和预测值基本吻合,最大残差绝对值为0.995 5mm.最小为0 mm,平均残差为0.331 1 mm.通过累减还原得到模型预测值,进而计算模型相对误差和绝对误差可知:绝对误差最小为0 mm,最大为0.900 5 mm,相对误差最大达24.34%.

同理,可建立不同维数的预测模型,各维度模型参数及精度评定结果见表5.

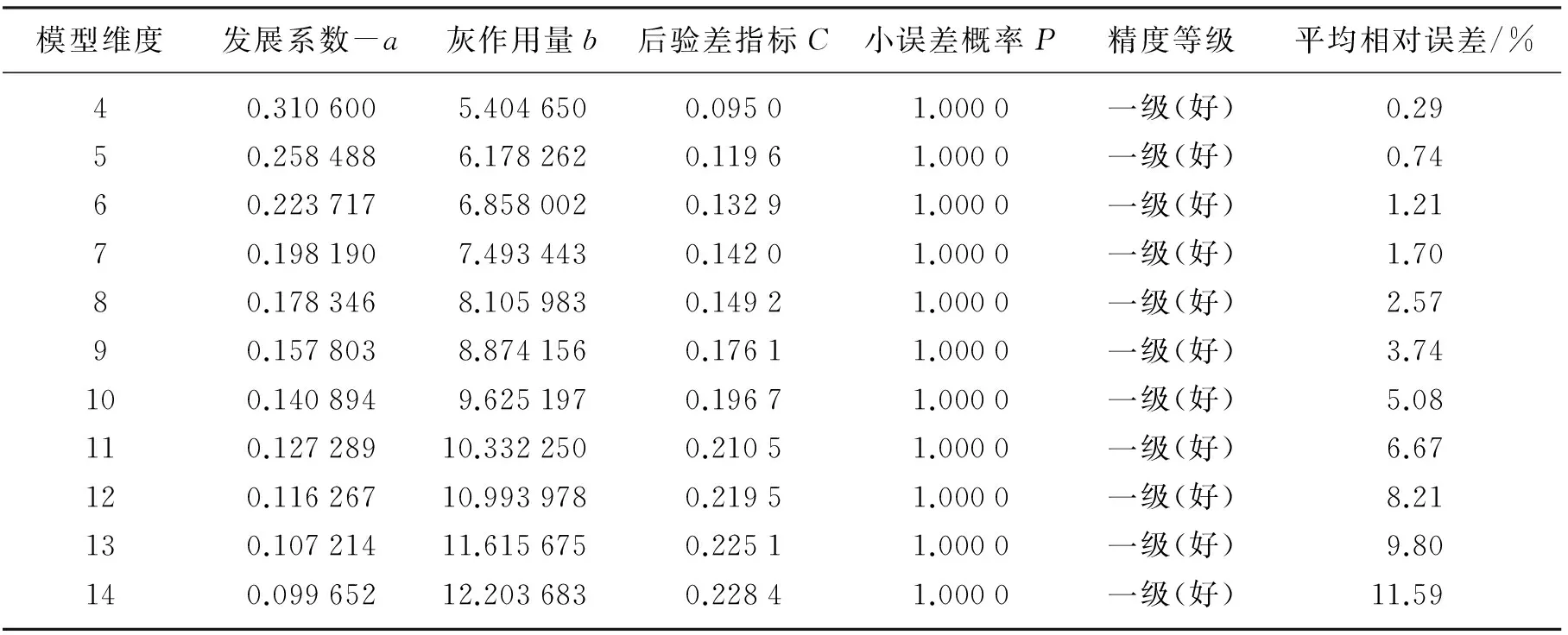
表5 4～14维GM(1,1)模型参数及精度评定结果Table5 The parameters and accuracy assessment results of different dimension GM(1,1) models

从表5可以看出,建立的4～14维GM(1,1)模型从中选择预测精度最好的模型进行沉降量预测,通过比较可知,选择不同的数据维数,发展系数-a,灰作用量b的值也不一样,后验差指标C值平均相对误差各不相同.随着参与建模的数据维度的增加发展系数-a呈现递减的趋势,而灰作用量b、后验差指标C以及平均相对差均呈现增大的趋势,唯独相同的是P值均为1,表明这些参数所建立模型的精度均达到了一级水平,尤以4维GM(1,1)模型平均相对误差最小为0.29%,适用于短期预测,其预测效果较好,说明预测基坑周边地表沉降,并不是数据越多建立模型预测值与实测值越接近,沉降监测结果越可靠.

为了提高精度,本文选用4维,第4次残差序列建立GM(1,1)模型为

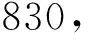
(6)

模型参数-a=0.362 364,b=0.000 663.其平均相对误差为0.02%,根据后验差指标C和小误差概率P对模型进行检验,当P=1>0.95和C=0.004 4<0.35时,精度等级为好,表明模型可靠.由此推算预测值如表6.

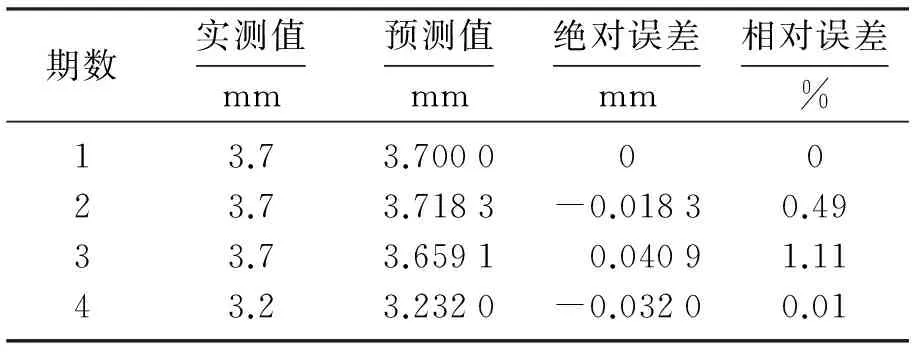
表6 4维残差模型实测值与预测值Table 6 The measured values and forecasted values of residuals model

如表6所示,4维残差序列模型的预测值与实测值非常接近,满足短期预测所需.其绝对误差均小于0.05 mm,相对误差最大为1.11%,满足较高精度要求.沉降实测值均小于4 mm,说明沉降比较稳定.

3 结 论

本文引入了灰色系统理论,根据地铁车站基坑周边地表沉降监测点实测数据,通过累加生成数据列,建立微分方程,进而对模型参数求解,还原预测值,建立GM(1,1)预测模型.通过预测模型可了解周边地表沉降变形情况,不仅仅节约了长期观测的费用,还能及时反馈到设计中,指导地铁施工,基于本文研究得到以下结论:

(1) 在地铁工程施工过程中,地铁车站基坑工程中一个周边地表沉降监测点的14期实测数据分析可知,该点累计沉降量高达39.8 mm,其中最大沉降量为3.7 mm,最小为2.1 mm,平均沉降量2.8 mm/d,表明地表沉降点略有下沉,但变化速率不大,沉降趋于稳定.

(2) 依据实测数据建立4维GM(1,1)模型x(1)(k+1)=21.100 725e0.310 600k+(-17.400 725),其预测精度达到一级,适用于短期预测,根据所建模型可得沉降监测点的累计沉降观测值和预测值基本吻合,模型通过精度评定,其绝对误差最小为0 mm,最大为0.900 5 mm,满足较高精度要求.为了提高精度选用4维,第4次残差序列建立GM(1,1)模型式(6),其平均相对误差为0.02%,模型通过检验,精度等级为好.表明模型可靠.由此推算预测值与实测值吻合非常好,沉降实测值均小于4 mm,而预测值平均值不超过4 mm,说明沉降比较稳定.

(3) 分别构建4～14维GM(1,1)模型,所建立不同维4～14维GM(1,1)模型均能通过精度评定,且预测精度达到一级,其中以4维模型的平均相对误差最小.基于平均相对误差最小的GM(1,1)建模,适用于短期预测,所建立的4维GM(1,1)累计沉降预测模型,最大残差绝对值为0.995 5 mm,最小为0 mm,平均残差绝对值为0.331 1 mm,平均相对误差为0.29%.

较5～14维模型而言,可以获得更为满意的预测结果.在实际建模过程中,选择不同的数据维数建立模型,模型参数各不相同,并不是原始数据序列的数据都用来建模,通过比较4～14维的GM(1,1)模型可知针对预测基坑周边地表沉降变形,建模过程中所需监测数据少,实际建模时,并不是参与建模的原始时间序列数据越多,模型精度就越好,证明了在基坑周边地表沉降变形分析中应用灰色预测法的可行性.

[1] 蒋万军,张庆贺,张文才.长条形地铁车站开挖时周边地表沉降规律及控制措施[J].建筑技术开发,2007,34(7):17-19.

(Jiang Wanjun,Zhang Qinghe,Zhang Wencai,et al.Disciplinarian and the Controlling-Measurement for the Surface Settlement in the Excavation of Long-Strip Metro Pit in Shanghai[J].Building Technique Development,2007,34(7):17-19.)

[2] 张文翔,瞿成松,刘毅,等.灰色模型在基坑工程地面沉降预测中的应用[C]∥地下交通工程与工程安全:中国国际隧道工程研讨会文集,2011:857-863.

(Zhang Wenxiang,Qu Chengsong,Liu Yi,et al.Based on Grey Model for the Surface Settlement around Foundation Pit[C]∥Underground Transportation Projects and Work Safety: Proceedings of China 5th International Symposium on Tunnelling,2011:857-863.)

[3] 刘思峰.灰色系统理论及其应用[M].北京:科学出版社,2000:105-110.

( Liu Sifeng.Grey System Theory and Application[M].Beijing: Science Press,2000:105-110.)

[4] 吴杰,柏林,左工,等.多因素灰色G(1,N)模型及其在基坑位移预测中的应用[J].测绘科学,2012,37(6):178-180.

(Wu Jie,Bo Lin,Zuo Gong.Based on Grey Multi Factor GM (1,N) Model and its Application in the Foundation Pit Deformation Prediction[J].Science of Surveying and Mapping,2012,37(6):176-178.)

[5] 卢志刚,张建栋,刘兴权.基于GM(2,1)模型的基坑变形预测分析[J].科技通报,2013.29(7):103-108.

( Lu Zhigang,Zhang Jiandong,Liu Xingquan.Pit Deformation Prediction Analysis Based on GM(2,1) Model[J].Bulletin of Science Technology,2013,29(7):103-108.)

[6] 陈晓斌,张家生,安关峰.GM(1,1)与GM(2,1)模型在基坑工程预测中的应用[J].岩土工程学报,2006(S):1401-1405.

(Chen Xiaobin,Zhang Jiasheng,An Guanfeng.Application of Gray-Method Models G(1,1) and G(1,2) Forecasting of Pit Excavation Engineering[J].Chinese Journal of Geotechnical Engineering,2006,28(S):1401-1405.)

[7] 梅正阳,韩志斌.数学建模教程[M].北京:科学出版社,2012:85-90.

( Mei Zhengyang,Han Zhibin.Mathematical Modeling Tutorial[M].Beijing: Science Press,2012:85-90.)

[8] 张雷,杨海鸣.灰色预测分析开挖基坑周边地表的沉降[J].路基工程,2008(6):142-143.

(Zhang Lei,Yang Haiming.Application of Grey Forecasting Method to the Surface Settlement in the Excavation of Foundation Pit[J].Subgrade Engineering,2008(6):142-143.)

[9] 邓华灿,陈松林.基于灰色序列GM(1,1)模型的建设用地预测[J].沈阳大学学报.2007,19(2):100-102.

(Deng Huacan,Chen Songlin.Predication of Constructed Land Based on Grey Model(1,1)[J].Journal of Shenyang University,2007,19(2):100-102.)

[10] 胡冬,张小平.基于灰色系统理论的基坑变形预测研究[J].地下空间与工程学报,2009.5(1):74-78.

(Hu Dong,Zhang Xiaoping.Research on Predicting Deformation of Foundation Pit Based on Grey System Theory[J].Chinese Journal of Underground Space and Engineering,2009,5(1):74-78.)

【责任编辑: 胡天慧】

Application of Different Dimension GM (1,1) Model in Prediction of Foundation Pit Ground Settlement

ZhengLi1,BaiBaoyu2

(1.School of Environment and Survey Engineering,Suzhou University,Anhui 234000,China; 2.Science Information Office of Chongqing Police,Chongqing 400000,China)

Based on foundation pit surrounding ground settlement data of subway engineering,the grey system theories are employed.By establishing the different dimension GM (1,1) prediction models,ground surface settlement of foundation pit were forecasted and analyzed.Use residuals and the posterior variance validation to the reliability of the model outcome,the exemplified result shows that the feasibility of grey model to forecast ground surface settlement of foundation pit is verified.The result shows that in constructing different dimension GM (1,1) model,as the number of data dimension grows,the parameter a is decreased,but the parametersb,Cand the average relative error are increased,different dimension model all has high precision achieve the level of the standard 1.The calculating results of four dimension GM (1,1) model accordance well with those experimental observation of surrounding ground settlement,it is suit short-term prediction demand.So,the required data for modeling the ground surface settlement needed are relatively less,which can save the cost for long-term observation and provide an important theoretic basis.

foundation pit engineering; different dimension GM (1,1); ground surface settlement; prediction

2015-01-09

宿州学院安徽省煤矿勘探工程技术研究中心开放课题资助(2013YKF04); 宿州学院校级项目(2011yss03).

郑 丽(1983-),女,江苏洪泽人,宿州学院讲师.

2095-5456(2015)04-0277-06

P 258

A