基于实验和数值方法的橡胶材料本构模型分析

李 炼,潘盛山

(大连理工大学 建设工程学部,辽宁 大连 116024)

基于实验和数值方法的橡胶材料本构模型分析

李 炼,潘盛山

(大连理工大学 建设工程学部,辽宁 大连 116024)

为探寻目前用于土木工程减隔震方面的基于唯象理论的Neo-Hookea模型、Mooney-Rivilin模型和Yeoh模型三种橡胶本构模型在有限元分析中的匹配程度,先对橡胶进行静力加载实验,然后通过实验数据处理得到三种本构模型各自的参数,并将三种模型参数分别代入到有限元软件进行分析计算,最后将得到的三种模型下的计算结果与实验数据对比.分析结果表明,在橡胶压缩时,Neo-Hookea模型适用于压应变为0～45%的范围,Mooney-Rivilin模型和Yeoh模型适用于压应变为≥60%的范围.研究对橡胶压缩时如何选择本构模型做出了解答,过程中所采用的研究方法和研究结果也有一定的借鉴意义和实用价值.

橡胶; 本构模型; 加载试验; 有限元模拟; 静态特性; 参数

目前橡胶材料在工程中应用广泛,在建筑材料领域有利用其制成轻质、弹性好、韧性高、抗冲击的橡胶混凝土[1],在结构减隔震领域有利用其超弹性和黏弹性来研发减隔震装置.现如今在结构减隔震领域里,橡胶构件的设计中主要采用一些复杂的数值技术.随着计算力学的发展和橡胶在工程中应用的日渐广泛,需要采用更精确、实用且能与有限元理论相融合的本构模型[2].基于连续介质力学唯象理论,橡胶常用的本构关系模型有N次多项式模型和Ogden模型,通过实验方法获得相关模型参数是对橡胶制品进行性能分析的关键所在[3].在这两种模型中,N次多项式模型使用范围广,可通过改变多项式阶数和系数以适应小、中、大各阶段的应变,如Neo-Hookea模型、Mooney-Rivlin模型和Yeoh模型.而Ogden模型更多的用于拉伸情况下的超大应变的模拟,应变水平可达到700%.该模型拥有更高阶的参数,需要在拟合时提供足够多的实验数据,但同时也容易出现拟合数值困难.鉴于此,本文主要以适合中小应变的N次多项式模型为研究对象,通过对橡胶制品进行静力加载试验,并运用Origin软件进行实验数据处理,求得各类本构关系的参数后在ANSYS软件中进行数值分析,将实验结果与数值计算结果进行对比验证,以了解各本构模型与数值计算的契合程度,为工程应用提供借鉴.

1 橡胶本构关系理论

实验所用的材料是典型的超弹性材料,是由共价键连接而成的长链分子物,分子链之间在许多节点上通过化学键相连而成,并形成交联网络结构[4].理论上通常采用应变能函数W=W(I1,I2,I3)来对该类超弹性材料的物理性质进行表达,其中I1,I2,I3是Green应变张量第一、第二和第三主不变量.对于单位立方体块,如果受力后变成边长分别为λ1,λ2,λ3的长方体,则[5]

(1)

又对于不可压缩材料,

(2)

故

(3)

因为单轴压缩时另两个方向自由,设压缩应变为ε,则有

(4)

将式(2)、式(4)代入式(1)可得:

(5)

将式(5)代入应变能关系式并对应变张量求导可得到单轴压缩时橡胶应力应变关系式[6]

(6)

(7)

(8)

下标NH1、MR1、Y1分别对应Neo-Hookea模型、Mooney-Rivilin模型和Yeoh模型.CNH1、C10、C1等为各模型对应的参数.

2 橡胶圆柱体实验

2.1 实 验

传统的橡胶实验为了确定橡胶材料的应变能函数以及对应的参数,在考虑橡胶完全或近似不可压缩的前提下,需对橡胶进行三种模式的实验[7]:单轴向拉伸实验;平面剪切实验;等双轴拉伸实验.

本实验由于条件所限,没有采取传统的实验方法,而是对橡胶进行单轴压缩试实验[8].实验橡胶为天然橡胶,其硬度为60,将其制成直径为0.2 m,高为0.2 m的圆柱体试件.实验时橡胶柱上下表面各垫有传压钢板以及光滑的有机玻璃板以起到减小摩擦的作用.将制成的试件放在WAW-1000B微机控制电液伺服万能实验机上进行静载压缩,在室温条件下以20 mm/min的速度施加竖向压缩位移,当位移达到129 mm时停止加载.如此反复连续加载卸载共三次,前两次可视为实验机调节,记录最后一次应力应变数据值.前后一共进行了三组实验,取三组实验的平均值作为最后的实验值.

实验数据如表1所示.

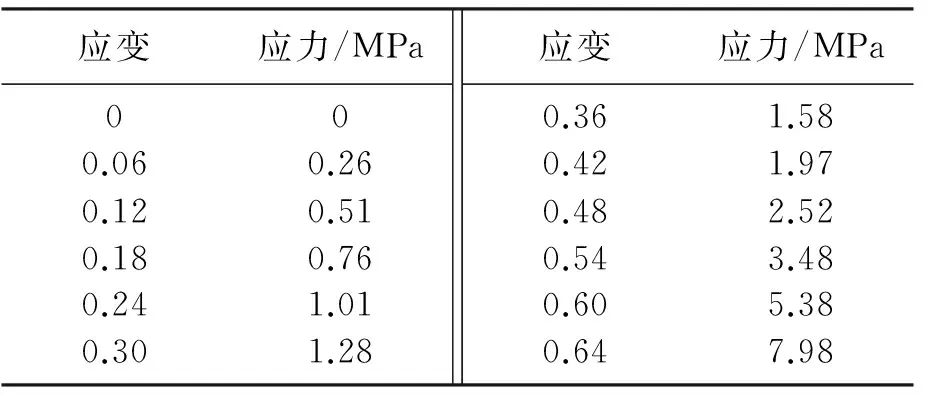
表1 单轴压缩实验数据Table1 The experimental data of uniaxial compression

导出实验数据运用Origin进行处理,得到曲线如图1所示.

实验所测得的应力

(9)

式中:F为所受载荷;A0为初始受压面积.

实验所测得的应变

(10)

式中:Δl为压缩量;l0为初始高度.

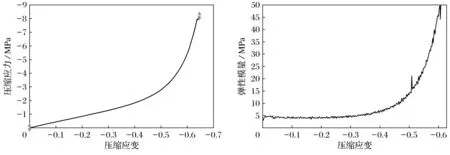
图1 实验数据点曲线Fig.1 The curve of experimental data point

绘制的曲线为名义应力应变曲线.由于在ANSYS中所得的结果均采用的是Cauchy应力与Cauchy应变(即真应力与真应变),所以在读取ANSYS计算结果时需要将对应的真应力、真应变转化为对应的名义应力和名义应变.它们之间换算关系为[9]

(11)

(12)

式中,σtrue,εtrue,σnom,εnom分别为真应力、真应变、名义应力、名义应变.

2.2 参数拟合

通过实验得到应力应变区,先后用Origin软件进行该曲线拟合,如图2所示,拟合目标方程为式(6)～式(8).

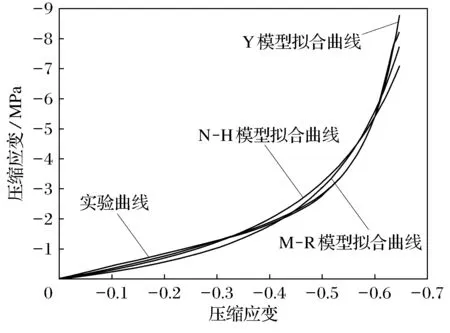
图2 拟合曲线图

拟合结果以及所得各参数如下:

N-H模型CNH1=0.458,拟合曲线相关系数R=0.973 6;

M-R模型C10=0.272,C01=0.080 8,拟合曲线相关系数R=0.983 8;

Y模型C1=0.529,C2=-0.097,C3=0.025,拟合曲线相关系数R=0.998 5.

3 有限元数值模拟

用ANSYS有限元分析软件进行数值模拟时,橡胶单元采用Solid185单元,该单元用于3D实体结构,可模拟几乎不可压缩材料的弹塑性行为和完全不可压缩材料的超弹性行为,其材料属性分别按照Neo-Hookea模型、Mooney-Rivilin模型和Yeoh模型进行定义.为了方便计算,由于圆柱体的对称性,只建1/4圆柱模型.建模时在模型底面施加竖向约束,在顶面施加向下的强制位移载荷(129 mm).如图3所示.

算完后通过/post26时间历程后处理导出各本构模型对应的应力应变结果,按照式(11)、式(12)转为名义应力和名义应变并与实验所得数据进行对比,如图4所示.

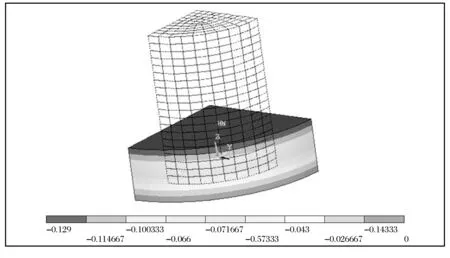
图3 ANSYS橡胶有限元模型图Fig.3 The finite-element model of rubber

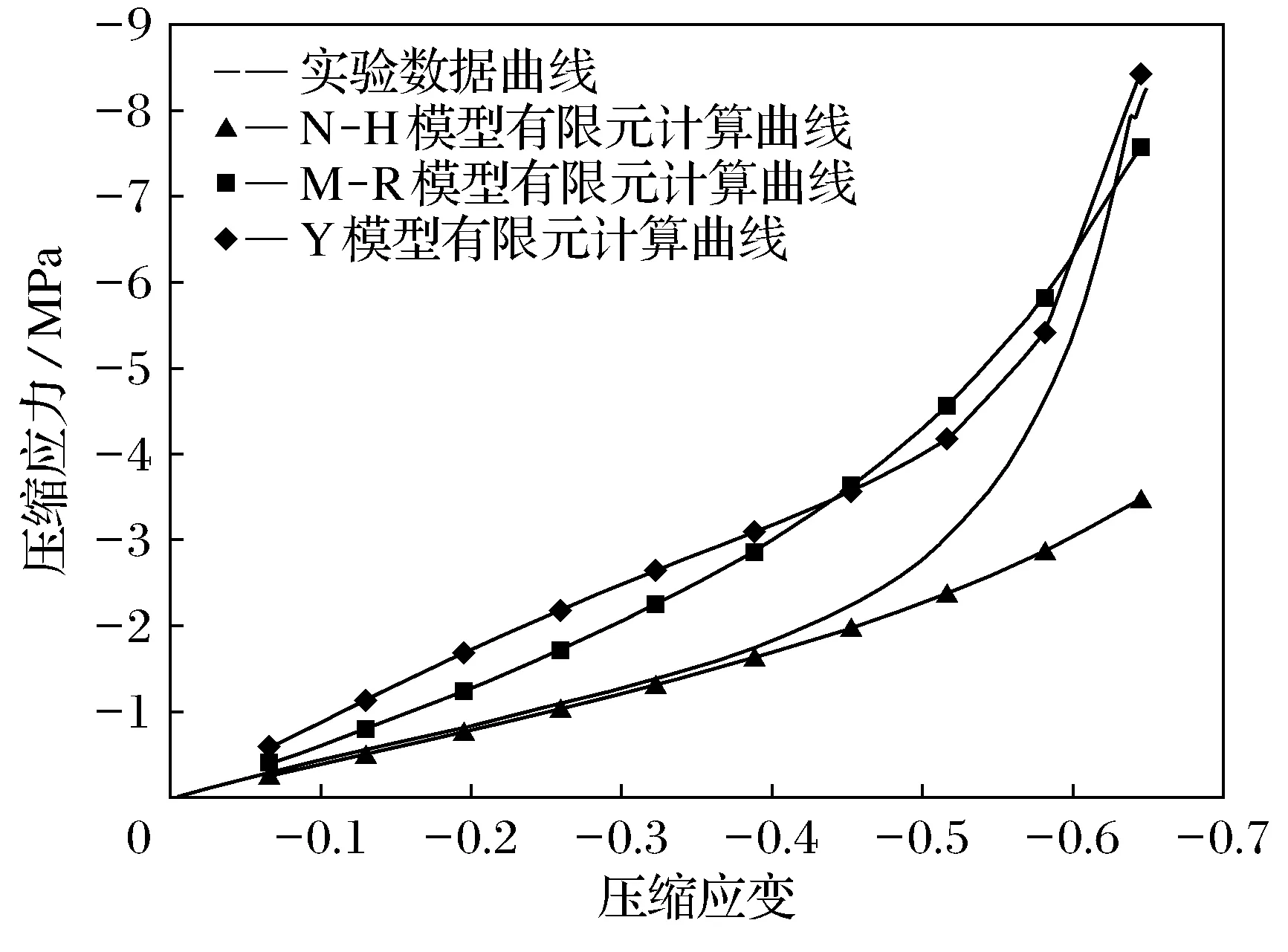
图4 实验与有限元结果对比图Fig.4 The comparison chart of the finite-elementresult and experiment data

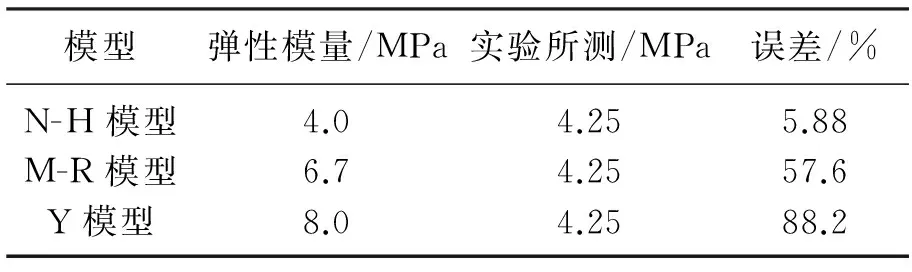
表2 初始弹性模量对比表(0≤ε≤0.3)Table2 The comparison Tableof the initial elastic modulus

表3 有限元数据与实验数据对比表Table3 The comparison Tableof the finite element value and the experiment value

续表3

应变实验应力/MPaN-H应力与实验应力差/MPaM-R应力与实验应力差/MPaY应力与实验应力差/MPa0.3871.742-0.1221.1131.3400.4522.233-0.2691.3621.3010.5163.029-0.6661.5011.1240.5814.617-1.7691.1630.7500.6458.244-4.772-0.6680.190

将上述各个模型应力与实验应力差形成的数组求二范数(记范数1),同时取各组前5个数组成的数组,再求一次二范数(记范数2).

范数1: ‖NH‖2=5.14; ‖MR‖2=2.92; ‖Y‖2=3.05.

范数2: ‖NH‖2=0.125; ‖MR‖2=1.17; ‖Y‖2=1.99.

对实验和数值分析的结果进行总结.

(1) 橡胶在刚开始受压时(ε≤0.3)本构关系呈线性,其初始弹性模量约为E=4.25 MPa.当应变ε≥0.5时弹性模量急剧增大,说明在中等应变的时候橡胶已经开始进入压缩硬化状态,应力应变关系不再是线性.

(2) 在运用Origin对三个理论本构关系式进行拟合时发现,单从曲线整体上看,三拟合曲线都能与实验数据曲线较好地匹配.从曲线相关系数来看,Yeoh模型结果最好,Neo-Hookea模型最差.

(3) 通过对有限元计算值与实验数据对比得出的初始压缩刚度和二范数可知,Neo-Hookea模型在小应变阶段(0≤ε≤0.45)几乎与实验数据重合,能十分完好地模拟出其应力应变关系;而当进入到中等应变阶段(ε≥0.6)后,Mooney-Rivilin模型和Yeoh模型开始逐渐与实验数据曲线靠近,其中Yeoh模型效果更好.故在进行数值分析时,若是对橡胶进行小应变的压缩(ε≤0.45),可采用Neo-Hookea模型且能得到很好的结果;若是处在中等应变阶段(ε≥0.6),用Mooney-Rivilin模型和Yeoh模型进行模拟较合适.

4 工程实例分析

为了验证上述三类本构关系的实用性,以大连理工大学桥梁工程研究所某次板式橡胶支座实验为例进行分析.该板式橡胶支座为实验所用支座组中的一个,所用橡胶与前面做压缩实验所用的橡胶属同一厂家生产,均为天然橡胶,规格也相同.支座橡胶层为三层,每层厚度35 mm,长宽均为600 mm.内加劲钢板层共两层,每层厚度10 mm,长宽均为600 mm,顶底面钢板层厚度为20 mm,长宽均为700 mm.支座模型如图5.

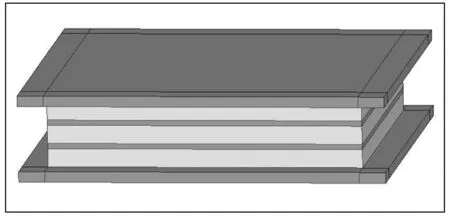
图5 板式橡胶支座有限元模型图Fig.5 The finite-element model of laminaterubber bearing

建模时钢板采用Solid65单元,弹性模量为210 GPa,泊松比υ=0.3;橡胶采用Solid185单元,分别采用Neo-Hookea模型、Mooney-Rivilin模型和Yeoh模型来定义其材料属性.为了验证支座的压缩性能,在支座顶层钢板施加6 MPa的压应力,通过有限元计算后得出对应于橡胶各个本构模型下的支座竖向位移.

ΔY=3.58mm.

同时,依据JTGD62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》中规定,橡胶支座的抗压弹性模量和形状系数按下式计算:

式中:Ee为支座抗压弹性模量(MPa);S为支座形状系数;Ge为支座剪变模量,常温下Ge=1.0 MPa;lo a、lo b分别为支座加劲钢板短边和长边尺寸.当支座顶面施加6 MPa压应力时,由规范中公式计算支座竖向位移为Δ0=10 mm.

将有限元计算值与理论计算值对比见表4.

由表4可看出,在板式橡胶支座的有限元模拟中,采用Neo-Hookea模型对支座橡胶层进行模拟更为接近理论值,而Mooney-Rivilin模型和Yeoh模型计算所得误差都较大,这也与前面得出的三种本构模型在模拟小应变状态下橡胶的受力情况吻合.

该工程实例所得的结果与前面所得橡胶三种本构关系的结论相一致,很好地解释了在板式橡胶支座受压时橡胶层采用何种本构模型更为适合.事实上,由于JTGD62—2004《公路钢筋混凝土及预应力混凝土桥涵设计规范》中规定板式支座最大压应力不超过10 MPa,所以在使用时支座的竖向变形都是很小的,工程中板式橡胶支座在受力时更多的需要橡胶层提供较大的横向剪切应变而不是竖向应变.根据本文前面得到的结论,在板式橡胶支座中采用Neo-Hookea模型来模拟橡胶层是合理的,也是与实际情况相符的.

表4 竖向位移值对比表Table4 The comparison Tableof the vertical displacement

5 结 语

本次实验的结果数据仅限于本实验所用橡胶,由于实验过程中存在摩擦力、实验加载速度等多方面因素的影响,实验结果与有限元计算存在一定的偏差,但是仍从整体上对有限元计算中如何选取本构模型给出了相应的分析和回答,具有一定的普适性.本文在研究过程中采用了由实验到理论再到数值计算的研究方法.首先对橡胶进行静力加载实验得到应力应变关系曲线,然后通过已有的橡胶本构关系理论来得到与实验数据相符合的三种常用的应力应变关系式,再将得到的应力应变关系式代入到有限元中进行数值计算,最后将实验结果与数值结果进行对比.与此同时,本文还将所得的结论用于工程实例中,发现所得结论能很好地与工程实例结果相吻合,这也从一定程度上反映了该研究成果的意义.总体上说来,本文的研究结果表明了橡胶压缩时与各类本构模型相适应的程度,结论具有一定的借鉴意义,对工程实践也具有指导作用.在后续的研究中,将进一步分析橡胶加载、卸载时的应力应变曲线,通过应力应变滞回曲线结合有限元数值计算的方法考察橡胶的黏滞性,探寻橡胶的减隔震性能以为开发新的橡胶类减隔震产品提供理论基础.

[1] 杨春峰,杨敏,叶文超.改性方式对橡胶混凝土力学性能的影响[J].沈阳大学学报:自然科学版,2012,24(3):78-81.

(Yang Chunfeng,Yang Min,Ye Wenchao.Influence of Modification to Mechanical Properties of Waste Rubber Concrete[J].Journal of Shenyang University: Natural Science,2012,24(3):78-81.)

[2] 危银涛,方庆红,金状兵,等.填充橡胶本构模型研究进展[J].高分子通报,2014,5(5):15-21.

(Wei Yintao,Fang Qinghong,Jin Zhuangbing,et al.Research Progress on Constitutive Model of Filler Rubber[J].Chinese Polymer Bulletin,2014,5(5):15-21.)

[3] 刘锋,朱艳峰,李丽娟,等.橡胶类材料大应变硬化的本构关系[J].华南理工大学学报:自然科学版,2006,34(4):9-12.

(Liu Feng,Zhu Yanfeng,Li Lijuan,et al.Constitutive Law of Hardening Rubber-Like Material with Large Strain[J].Journal of South China University of Technology: Natural Science Edition,2006,34(4):9-12.)

[4] 李忱.超弹性体非线性本构理论[M].北京:国防工业出版社,2012:9.

(Li Chen.The Constitutive Theory of Hyper Nonlinear Elastic Body[M].Beijing: National Defence Industry Press,2012: 9.)

[5] Treloar L R G.The Physics of Rubber Elasticity[M].3rd Edition.Oxford: Clarendon Press,1975.

[6] 王丽丽.超弹性材料参数的测定及在微管吸吮模型中的应用[D].太原:太原理工大学,2013,R318.08:16-18.

(Wang Lili.The Determination of Hyperelastic Material Parameters and the Application in the Micropipette Aspiration Experiment Model[D].Taiyuan: Taiyuan University of Technology,2013.)

[7] 刘文武,朱石坚,楼京俊,等.确定橡胶材料应变能密度函数的一种新方法研究[J].振动与冲击,2007,26(7):1-5,9,176.

(Liu Wenwu,Zhu Shijian,Lou Jingjun,et al.A New Research Method to Determine the Strain Energy Density Function of Rubber Material[J].Journal of Vibration and Shock,2007,26(7):1-5,9,176.)

[8] 伍开松,徐大萍,严永发,等.橡胶大变形不可压缩方法试验数据处理[J].橡胶工业,2013,60(7):400-403.

(Wu Kaisong,Xu Daping,Yan Yongfa,et al.Data Processing Method of Rubber Testing Based on Incompressible Large Deformation Analysis[J].China Rubber Industry,2013,60(7):400-403.)

[9] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].2版.北京:机械工业出版社,2006.

(Shi Yiping,Zhou Yurong.The ABAQUS Finite Element Analysis Example[M].Beijing: China Machine Press,2006.)

【责任编辑: 祝 颖】

Constitutive Model of Rubber Material Based on Experiment and Numerical Method

LiLian,PanShengshan

(Faculty of Infrastructure Engineering,Dalian University of Technology,Dalian 116023,China)

To study the matching degree of Neo-Hookea model,Mooney-Rivilin model and Yeoh model,which are based on phenomenological theory and used in seismic mitigation and absorption,in finite element analysis,the static loading test on rubber were done,then the respective parameters of each constitutive model were got by processing the experimental data,and the parameters of the three models were substituted into the finite element analysis software to analysis and calculate.The results show that,when the rubber is compressed,Neo-Hookea model is suiTablefor a range of 0～45% of compressive strain,and the Mooney-Rivilin model and Yeoh model is suiTablefor compressive strain of more than 60%.This research explained the choosing of constitutive model for rubber compression,and the research methods and results used in the process also has a certain significance and practical value.

rubber; constitutive model; loading test; finite-element simulation; static characteristics; parameters

2015-01-31

国家自然科学基金资助项目(51108058).

李 炼(1987-),男,湖北黄冈人,大连理工大学硕士研究生.

2095-5456(2015)04-0267-06

TU 533

A