村级居民点离散度评价模型及其与农村经济关联分析

杨 思 遥，王 艳 慧，李 贺 颖

(首都师范大学资源环境与地理信息系统北京市重点实验室,北京 100048；首都师范大学三维信息获取与应用教育部重点实验室,北京 100048；首都师范大学城市环境过程与数字模拟国家重点实验室培育基地,北京 100048)



村级居民点离散度评价模型及其与农村经济关联分析

杨 思 遥，王 艳 慧*，李 贺 颖

(首都师范大学资源环境与地理信息系统北京市重点实验室,北京 100048；首都师范大学三维信息获取与应用教育部重点实验室,北京 100048；首都师范大学城市环境过程与数字模拟国家重点实验室培育基地,北京 100048)

量化居民点空间分布离散度并探索其与农村经济指标的关联关系，以期为“整村推进”扶贫开发规划的实施提供指导意见。以国家扶贫重点县——鹤峰县为研究区，以行政村为评价单元，分别从人文和自然角度引用离散度综合指数(DCI)和景观综合指数(LCI)结合空间探索性分析方法，对比分析鹤峰县居民点空间分布的离散特点，并采用线性回归模型和空间滞后回归模型剖析鹤峰县整体及不同自然与经济条件下离散度与农民人均纯收入之间的相互影响关系。研究结果表明：1)整体上，DCI与LCI均存在空间聚集效应，但两者空间分布特征存在差异，DCI评价结果介于0.59～4.56，LCI评价结果介于0.14～2.61，DCI可以更好地反映离散度。2)通过空间滞后回归模型对DCI与农民人均纯收入分析，得到两者间呈明显相关关系。3)DCI与道路密度、经济圈层、坡度均存在相关关系，同时反映收入变化趋势；LCI在经济圈层等级下未表现出此特征。对于“整村推进”扶贫项目的实施，既要重视道路等人文要素的影响，也要考虑行政村之间的联系。

离散度；景观指数；农民人均纯收入；居民点；空间分布格局；鹤峰县

0 引言

居民点是人们共同生活和进行经济、政治和文化等活动而聚集的定居场所[1]。居民点空间分布状况是一个区域自然、社会、经济以及历史发展的综合反映，影响着区域经济发展的规模、方向以及发展的可能性[2]。行政村作为农村社会经济的基本统计单元是由若干居民点构成的。相比城市有规律的集中建设规划，一些偏远地区的居民点布局缺乏详尽的规划。多数居民围田造房，居民点分布离散，之间经济交流受到限制，这是导致农村大面积贫困的一个原因。定量揭示居民点分布规律有助于辅助相关部门基础设施布局、社会保障设施布局等的具体规划与实施，对于改善贫困山区居民的贫困状况、推进国务院《中国农村扶贫开发纲要(2011—2020)》中“整村推进”扶贫开发措施的实施具有重大意义。

在居民点空间分布方面，定性的研究不够精确，目前关注重心转移到居民点分布的定量研究上。孙华生等用GIS叠加分析、缓冲区分析等方法，分析了不同道路缓冲区、高程、坡度上的居民点分布特征，并提出了一系列居民点规划方案[1,3-6]；宋志军从分形的角度对居民点空间分布进行了评价[7]；周婧结合多种指数对贫困区居民点用地进行分析[8]，但都没有在行政村尺度下与经济状况相关联的分析。吴江国等基于景观分析软件计算景观格局指数，分析居民点分布特征[9-13]；王志彬等通过边界密度、最小距离指数等景观指数评价了不同景观类型之间的区别[14-16]，但其侧重点是不同的景观类型，未对某一具体景观类型做出详尽分析，且未考虑不同地理环境与社会经济条件(如地理位置、公共基础设施等)对不同斑块区域的影响。居民点空间分布离散程度作为区域差异程度的定量表达，其对微观尺度的区域协调发展和维持区域公平具有重要参考价值。李新运等选取重心距离、平均间距等指标基于欧式距离计算城市群中居民点的空间分布离散度[17,18]，但缺乏与经济状况的详细关联分析，并且欧式距离不能准确反映出两地之间的实际连通距离。李贺颖等根据改进的离散度综合指数(DCI)定量研究内乡县居民点空间分布离散度，并与农村居民纯收入做相关分析，得到DCI可以反映农村经济状况的结论[19]，但仅从人文角度分析评价，且未考虑DCI与表征贫困状况的核心指标——人均纯收入之间的关系。

本文以国家扶贫开发重点县——鹤峰县为研究区，分别从人文和自然角度评价居民点空间分布离散度，对比分析二者之间的区别，并详细剖析不同自然与经济条件下二者与农民人均纯收入之间的相互影响关系，以期为政府相关部门系统整治规划农村居民点提供参考。

1 研究区概况及数据源

1.1 研究区域概况

鹤峰县位于湖北省西南部，恩施州的东南部，与湖南省毗邻。鹤峰县是巴文化发祥地之一，是第二次国内革命战争时期湘鄂边革命根据地的中心，先后被定为国家一类老区县、国家扶贫开发重点县。鹤峰县辖9乡镇、203个行政村(去除无居民点区域)、23 422个居民点。县境东西长85 km，南北宽67 km，总面积2 892 km2，人口22.02万人。鹤峰县内地形西北高、东南低，多山间小盆地，平均海拔1 147 m，是湖北省的高山县之一；最高点是西北部的牛池，海拔2 095.6 m，最低点是东南角的江口，海拔194.6 m，高差达1 901 m。

1.2 数据来源及数据处理

本文所使用的数据包括基础地理数据和社会经济数据，具体包括：鹤峰县2010年的村界数据、居民点数据、根据Google Earth矢量化的道路数据、来自鹤峰县扶贫办的各行政村2010年统计数据(含各行政村的农民人均纯收入数据)。所有数据在使用前均进行了裁剪、数据导入、地理配准等预处理。

2 研究方法

本文计算居民点空间分布离散度的方法，一方面引用李贺颖提出的离散度综合指数(DCI)[19]，另一方面从常用的景观指数中选取最适合描述居民点空间分布离散度的指数，组合构建景观综合指数(LCI)。从居民点空间分布离散度出发研究鹤峰县的居民点空间分布格局，从而验证DCI反映农村居民点空间分布离散程度的合理性，同时验证从居民点空间分布离散水平上反映农村经济状况的有效性。

DCI与LCI相近，两者均以行政村为评价单元，所不同的是：DCI基于道路网络连通距离计算，在构建3个基于数理统计方法计算的内部指标的同时，通过3个外部指标兼顾了行政村整体与外部的联系，反映了人文因素对离散度的影响；LCI基于欧式距离计算，使用传统景观指数，仅反映行政村内部居民点的自然空间分布离散状态，结构相对简单。

2.1 离散度综合指数评价(DCI)

DCI基于道路距离，从人文角度构建，适合鹤峰县多山地的地貌特征，包含加权平均重心距离、加权平均间距、空间标准差3个内部指标，以及行政村整体距邻村的平均距离、距离最近县城、最近乡镇政府的距离3个外部指标。DCI综合了内外部因素，具有全局性，描述行政村整体的离散度，由于6个指标对DCI影响程度大小相同，因此等权重赋权，加权求和得到每个行政村的DCI指数，计算方法如下：

加权平均重心距离的计算公式为：

(1)

重心点坐标的计算公式为:

(2)

式中：di为居民点pi到行政村内居民点重心点(xg,yg)的距离，通过道路网络连通距离计算，ai为居民点pi(xi,yi)的面积。

加权平均间距的计算公式为：

(3)

dij=ai×d

(4)

式中：d为居民点i、j间的道路距离，ai同上，n为行政村内居民点个数。

此外，空间标准差取行政村内居民点两两之间道路距离的标准差。3个外部指标也通过道路距离计算。最终通过等权重赋权加权求和得到DCI。

DCI=∑(di×wi) (i=1,2,…,6)

(5)

式中：di分别代表6个指标，wi代表不同指标的权重。

2.2 景观综合离散度指数评价(LCI)

从景观格局指数中选取与离散度、破碎度相关的指数构建LCI，包括平均斑块面积(MPS)、边界密度(ED)、最小距离指数(NNI)。计算方法如下：

MPS用于评价居民点斑块破碎度，其数值越小代表区域内居民点破碎度越大。

MPS=A/N

(6)

式中：A代表居民点斑块总面积，N代表居民点斑块个数。

ED揭示居民点斑块的边界分割程度，数值越大所体现的居民点斑块的破碎度越大。

ED=L/A

(7)

式中：L代表斑块边界总长度，A同上。

NNI综合考虑了斑块间最小欧式距离因素和斑块密度因素，其数值越大，代表居民点斑块离散度越大。计算公式如下：

NNI=MNND/ENND

(8)

(9)

式中：MNND为每个居民点斑块与其最邻近斑块间的平均最小距离，N和A同上。

由于以上3个指数在本研究中对离散度指数的重要性一致，因此以等权重构建LCI。正向负向指标均标准化处理，得到的LCI数值越大，代表居民点的分布越分散。

LCI=MPS×W1+ED×W2+NNI×W3

(10)

式中：W代表权重，其他指标含义同上。

2.3 空间探索性分析方法

空间自相关性表示某一要素的值是否与其周边相邻区域的属性值相关[20]。在鹤峰县的应用中，正相关表示该行政村离散度指数的值与其周边行政村的离散度指数的变化趋势相同，负相关表示相反。本文中选用全局Moran′sI指数以及LISA聚类图进行分析。全局Moran′sI可从全局上判断鹤峰县各行政村间的DCI是否存在自相关性，大于0则存在空间自相关性，小于0则不存在自相关。LISA聚类图则在地图上具体显示某一行政村与周边行政村的相关性。这种自相关性也应用到具体的回归模型中，传统的线性回归方程仅能拟合自变量和因变量之间的关系，没有考虑变量自身的空间自相关性。空间滞后模型适合于处理空间数据，并且提供一个统计上合理的解决方法[21]，它不仅考虑自变量与因变量之间的关系，还将变量的空间自相关性考虑进去，从而使回归拟合结果更准确。

2.4 离散度-农村经济关联分析方法

本文选用农民人均纯收入这一表征贫困状况的核心指标反映行政村经济状况，并具体分析其与上述离散度指标的关联。在居民点空间分布离散度与经济发展的关联性分析中，一方面采用传统线性回归模型，通过拟合度R2判断相关性大小；另一方面应用空间滞后回归模型分析两者间的关联程度，通过修正后的拟合度R*2提高拟合结果的准确性。在研究尺度方面，一方面对鹤峰县203个行政村的离散度指数值与农民人均纯收入数据整体分析，另一方面划分不同自然、经济等级条件，对不同等级条件下离散度与人均纯收入的相关性进行分析。

3 研究结果与分析

3.1 鹤峰县农民人均纯收入、DCI、LCI分布

3.1.1 农民人均纯收入分布状况 在鹤峰县203个有统计数据的行政村中，人均纯收入介于700～7 519元，约1/4行政村的收入水平低于2 300元贫困线，约1/3行政村低于恩施市农民人均纯收入3 255元，且只有1个行政村高于湖北省农民人均纯收入5 832元。鹤峰县人均纯收入自西向东呈逐渐降低的趋势，距离市区越近经济发展状况越好，走马镇作为经济中心对区域经济水平有一定促进作用。

3.1.2DCI分布状况DCI值介于0.59～4.56，平均值为2.02，在ArcGIS10.2中，按NaturalBreaks分类法将DCI分为3个等级，叠加显示山体阴影(图1)，可看出：鹤峰县北部、东部、东南部、西部的小部分地区以及中部偏南地区，地形起伏度均较大，相应DCI值也较大，居民点空间分布离散，而乡镇政府及县城附近行政村的DCI值普遍低于周边地区。DCI的空间分异特征主要为：从城关到外围离散度等级增大。在GeoDa软件中分析DCI的空间聚集效应，得到图2所示LISA图。通过计算可知DCI的全局Moran′sI指数为0.50，且通过检验，因此DCI在空间上存在空间自相关性。DCI在中北部县城附近呈低低聚集状态，所覆盖的区域包括县城和中营乡、下坪乡、燕子乡、容美镇这些经济中心，该区域经济较发达，距离县城较近，道路较通畅，居民点呈大面积聚集状态分布，因而DCI数值较低。中南部有两个区域呈高高聚集状态分布，该区域距离乡镇政府和县城较远，交通不便，通过计算外部指标所占比重可知，3个外部指标贡献度达65%，DCI值总体较大。

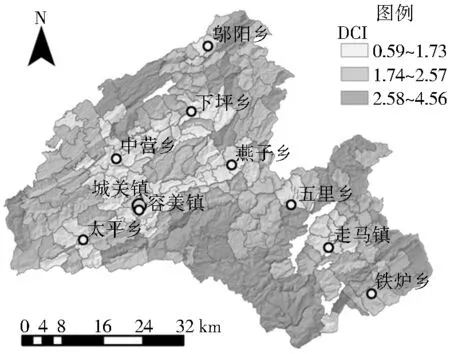
图1 鹤峰县DCI指数分布

Fig.1 The DCI index distribution of Hefeng County

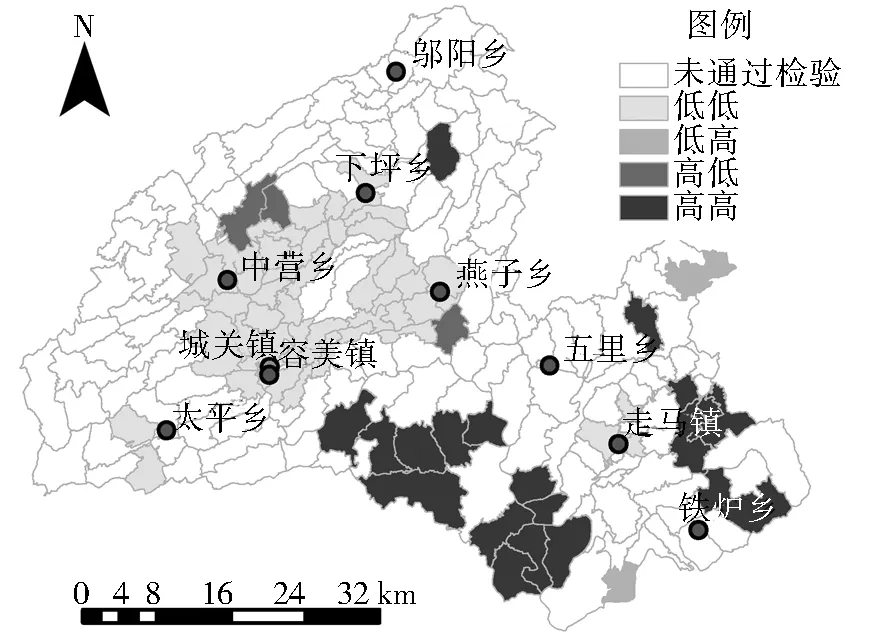
图2 鹤峰县DCI指数LISA聚类

Fig.2 LISA cluster map about DCI in Hefeng County

3.1.3 LCI分布状况 通过ArcGIS10.2统计得出，鹤峰县内居民点斑块总数为23 422个，居民点总面积33.47 km2，平均居民点斑块面积1 429 m2，居民点斑块数量多，平均面积小，分布散。同样以行政村为研究单元计算LCI，且按Natural Breaks分类法分为3个等级(图3)，发现LCI仅在鹤峰县9个乡镇政府附近和走马镇多数行政村范围内较低。LCI的空间分异特征主要为：离散度等级低值区分布于走马镇大部分区域及主要乡镇。在GeoDa软件中分析LCI的空间聚集效应，得到LISA图(图4)。通过计算可知LCI的全局Moran′s I指数为0.36，且通过检验，因此LCI也存在空间自相关性,高高聚集的区域为鹤峰县北部和城关镇东侧和西侧，低低聚集的区域为五里乡和走马镇大部分区域。

图3 鹤峰县LCI指数分布

Fig.3 The LCI index distribution of Hefeng County

图4 鹤峰县LCI指数LISA聚类

Fig.4 LISA cluster map about LCI in Hefeng County

对比图1和图3可看出，DCI与LCI除在乡镇政府附近数值均低于周边行政村外，二者的分布规律不尽相同。对比图2和图4可看出，虽然DCI与LCI均存在空间自相关性，但聚集区域完全不同。图2中，城关镇、中营乡和太平乡作为经济中心，其周围行政村离散度较低，该区域DCI表现出大面积低低聚集；但图4中LCI只存在小面积低低聚集，相反在走马镇附近存在大面积低低聚集。此外高高聚集的分布区DCI多集中于鹤峰县南部，LCI则多集中于北部。原因是DCI考虑外部指标，受乡镇位置影响，尤其城关镇的影响作用显著；而LCI不考虑经济中心位置，仅反映行政村内部的居民点分布状况，故表现出与DCI不同的聚集特征。

3.2 DCI、LCI与农民人均纯收入间关系

通过散点图及相关系数的方式分析离散度与农民人均纯收入的关联关系：以DCI为因变量、农民人均纯收入为自变量做线性回归分析，得到散点图，可看出DCI随着农民人均纯收入的增高而降低，拟合度R2为0.10，相关系数为-0.31，且通过检验，两者呈负相关关系。

由于DCI存在空间自相关性，根据普通线性回归模型得到的R2并不能很好地反映DCI与人均纯收入的关系，因此采用空间滞后回归模型考虑DCI的空间自相关性，得到的R*2值为0.46，大于线性回归模型的0.10，且通过检验。因此DCI不仅与人均纯收入相关，还与其周围行政村的DCI值有关，DCI与人均纯收入之间的关联关系采用空间滞后回归模型模拟更准确。R2值不很高的原因可能与恩施市的地理位置有关，另外当地的基础设施是否齐全以及当年是否发生自然灾害等都是影响人均纯收入的因素。同理计算LCI与农民人均纯收入之间的关联关系，根据相关系数R判断两者之间不存在相关性。由此看来，LCI虽然可以描述居民点的空间分布离散状态，但与行政村经济状况无相关性。

3.3 不同道路密度条件下DCI与收入、LCI间关系

行政村的经济状况往往与道路、交通状况相关，可用道路密度描述行政村的道路密集程度[22]。按Natural Breaks分类法将道路密度分成三类，分别统计不同道路密度等级下的DCI、LCI、收入的平均值(表1)。从表1看出：随着道路密度降低，DCI、LCI增大，收入降低。可见道路稀疏造成的交通不便加大了居民点分布的离散度，从而影响行政村经济。

表1 不同道路密度DCI、LCI及收入平均值

Table 1 The average value of dispersion and income in different road density

道路密度DCI均值LCI均值人均纯收入(元)高(4．17～8．18)1．551．653221中(2．63～4．17)2．001．773029低(0．77～2．63)2．501．872984

在每一道路密度等级内部对DCI、LCI与农民人均纯收入进行相关分析可得：LCI与收入之间不存在相关性，而DCI与收入之间存在相关性；由于DCI存在空间自相关性，结合空间滞后模型在3种道路等级下对DCI与农民人均纯收入进行空间滞后回归分析，相应拟合度R2在高、中、低道路密度下分别为0.22、0.37、0.29，均通过检验，在中等道路密度条件下拟合度最高，但数值均大于基于全县水平的线性回归拟合度0.10。因此，DCI不仅与人均纯收入有关，还与其空间自相关性有关，这不仅在整个鹤峰县范围内适用，在不同道路密度等级条件下也适用。

3.4 不同经济圈层条件下DCI与收入、LCI间关系

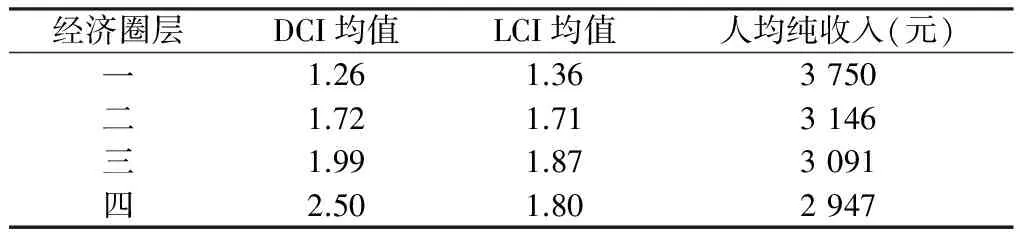
依据泰森多边形的邻近分析法，按距离经济中心(县城和乡镇政府所在地)远近将鹤峰县划分为4个经济圈层，距离经济中心最近的行政村为第一经济圈，距离经济中心最远的为第四经济圈，统计每个圈层的DCI、LCI和收入平均值(表2)。从表2看出：随着行政村距经济中心距离增大，受经济中心辐射作用变小，人均纯收入降低，DCI、LCI增大。但LCI的变化趋势在第四圈层发生改变，该圈层虽然距市区较远，但地势较平坦，利于大面积居民点集中建房，因此基于LCI计算的居民点离散度转而变小。

表2 不同经济圈层DCI、LCI及收入平均值

Table 2 The average value of dispersion and income in different economic circle

经济圈层DCI均值LCI均值人均纯收入(元)一1．261．363750二1．721．713146三1．991．873091四2．501．802947

3.5 不同坡度等级条件下DCI与收入、LCI间关系

地形地貌影响居民点的空间分布格局，坡度较陡的区域往往地质灾害多发，行政村经济状况也受到影响。因此依据表3等间隔划分平均坡度。鹤峰县多数行政村平均坡度大于15°，这可能也是导致鹤峰县整体贫困的原因之一。坡度增大会加大道路的曲折度，增大行政村之间的道路连通距离，影响居民点选址，因此DCI、LCI都随之增大，收入随之降低。LCI仅从区位角度分析居民点空间分布离散度，DCI还从人文角度分析离散度。坡度影响居民点的区位选择，区位对居民点离散度和农民人均纯收入均具有较强作用。

表3 不同平均坡度DCI、LCI及收入平均值

Table 3 The average value of dispersion and income under different average slope

坡度DCI均值LCI均值人均纯收入(元)5～15°缓坡1．921．53356515～25°斜坡1．981．74315925～35°陡坡2．161．922802

在斜坡地DCI也存在空间自相关性，对该区域的DCI和农民人均纯收入利用空间滞后回归模型进行回归分析，得到R2为0.44，大于基于全县水平的线性回归拟合度0.10。因此DCI与人均纯收入及其自身的空间自相关性有关，不仅在全县范围内适用，在不同坡度带内也适用。

4 结论与建议

本文选取人文、自然两种离散度指标计算方法对鹤峰县的居民点空间分布离散度进行评价，对比分析评价结果及其与农民人均纯收入之间的关系，并对比分析不同等级条件下DCI、LCI与农民人均纯收入之间的关联关系。得到以下结论：

(1)从人文角度构建的DCI对鹤峰县居民点空间分布离散度的评价结果为0.59～4.56，从自然角度构建的LCI评价结果为0.14～2.61，可见DCI在表征离散度中所含因素更全面，可更好地反映离散度。

(2)DCI和LCI均存在空间自相关性。DCI的空间分异特征表现为：道路密度越大、距离经济中心越近，地形起伏越小，DCI越小且呈现低低聚集分布，居民点空间分布越密集，反之DCI越大且呈高高聚集，居民点空间分布越离散；而LCI表现为道路密度越大、地形起伏越小，LCI越小，但在考虑经济圈层下第四圈层中与DCI不同，呈现出逐渐增大但在第四圈层转而变小的变化趋势。

(3)DCI与农民人均纯收入呈负相关关系，可以反映行政村的经济发展水平，且二者之间的关系通过空间滞后回归模型模拟更合理，拟合度为0.46；而LCI与行政村人均纯收入之间不存在相关性。通过进一步分级分析可知：DCI与农民人均纯收入在道路密度中等和平均坡度中等区域拟合度相对较高。

DCI、LCI两种指数均可用于居民点离散度评价中，两者分别从人文、自然角度构建，因此侧重点有所差异，造成了两种离散度指数与行政村经济状况关联性的差异。在行政村尺度上DCI与农村经济状况的关联性明显优于LCI，这也突出了道路要素的重要性，因道路曲折引发的交通不便也是导致贫困村贫困的重要原因之一。LCI在小尺度研究区的应用中存在局限性，会弱化居民点空间分布离散水平，但基于等级条件平均值可反映区域的经济状况，也说明区域人均收入与自然层面的居民点分布离散仍存在关联，贫困区相对集中的大面积居民点建立有利于区域经济的发展。DCI的优势也体现在行政村的外部关联中，重要乡镇、经济中心都对行政村经济的发展至关重要，如果要改善一个行政村的经济状况，应从更大范围的行政区域入手，考虑多方面要素的影响。因此，在扶贫的问题上应充分贯彻“整村推进”扶贫开发措施，同时也要考虑区域之间的联系，既要考虑自然要素的影响，也要重视道路等人文要素的影响。在规划具体居民点布局的同时，也应从行政区域整体状况及空间范围入手。

[1] 孙华生，黄敬峰，金艳，等.基于GIS技术的县域居民点空间分布特征分析及其优化布局[J].浙江大学学报，2007，33(3)：348-354.

[2] 梁会民，赵军.基于GIS的黄土塬区居民点空间分布研究[J].人文地理，2001，16(6)：81-83.

[3] 朱雪欣，王红梅，袁秀杰，等.广东省佛冈县城乡居民点空间格局优化研究[J].中国土地科学，2009，23(8)：51-57.

[4] 赵卫，沈渭寿，邹长新，等.雅鲁藏布江源头区居民点分布的影响因素[J].山地学报，2012，30(6)：728-736.

[5] 姜磊，雷国平，张健，等.农村居民点空间布局及优化分析[J].水土保持研究，2013，20(1)：224-229.

[6] ZHAO M D，TANG G A，SHI W Z，et al.A GIS-based research on the distribution of rural settlements in Yulin of northern Shaanxi[J].Journal of Geographical Sciences，2002，12(2)：171-176.

[7] 宋志军，关小克，朱战强.北京农村居民点的空间分形特征及复杂性[J].地理科学，2013，33(1)：52-60.

[8] 周婧，杨庆媛，信桂新，等.贫困山区农户兼业行为及其居民点用地形态[J].地理研究，2010，29(10)：1767-1779.

[9] 吴江国，张小林，冀亚哲，等.县域尺度下交通对乡村聚落景观格局的影响研究[J].人文地理，2013，28(1)：110-115.

[10] 从忆波，刘伟圣.秦安县农村居民点空间分布景观格局分析[J].地理空间信息，2011，9(5)：90-93.

[11] 潘竟虎，靳学涛，韩文超.甘谷县农村居民点景观格局与空间分布特征[J].西北大学学报，2011，41(1)：127-133.

[12] 刘颂，郭菲菲.基于景观格局分析的乡村居民点布局优化研究[J].东北农业大学学报，2010，41(11)：42-46.

[13] 于淼，边振兴，李建东.RS与GIS支持下的桓仁县农村居民点景观格局与空间分布特征分析[J].西南师范大学学报，2009，34(4)：106-114.

[14] 王志彬，王得祥，任广鑫，等.秦岭菜子坪林区森林景观格局及破碎化分析[J].西北农林科技大学学报，2011，39(12)：95-100.

[15] 杨瑞卿，薛建辉.城市绿地景观格局研究——以徐州市为例[J].人文地理，2006，20(3)：14-18.

[16] 谢军飞，李炜民，李延明，等.基于Patch Analyst的北京城市公园景观格局指数评价[J].城市环境与城市生态，2007，20(6)：14-16.

[17] 李新运.城市空间数据挖掘方法与应用研究[D].青岛：山东科技大学，2004.

[18] 冯维波，谢江沛，王伟伟，等.基于空间离散度的川渝城市群与长三角城市群的比较分析[J].城市规划，2012，7(1)：17-19.

[19] 李贺颖，王艳慧.贫困县村级居民点空间分布离散度及与农村居民纯收入关联格局分析[J].地理研究，2014，33(9)：1617-1628.

[20] 马国霞，徐勇，田玉军.京津冀都市圈经济增长收敛机制的空间分析[J].地理研究，2007，26(3)：590-598.

[21] 谢花林，刘黎明，李波，等.土地利用变化的多尺度空间自相关分析——以内蒙古翁牛特旗为例[J].地理学报，2006，61(4)：389-400.

[22] 范科红，李阳兵，冯永丽.基于GIS的重庆市道路密度的空间分异[J].地理科学，2011(3)：365-371.

Village Residential Dispersion Model and Its Association with Rural Economy

YANG Si-yao,WANG Yan-hui,LI He-ying

(1.BeijingKeyLaboratoryofResourceEnvironmentandGeographicInformationSystem,CapitalNormalUniversity,Beijing100048;2.KeyLaboratoryof3-DimensionalInformationAcquisitionandApplication,MinistryofEducation,CapitalNormalUniversity,Beijing100048;3.StateKeyLaboratoryIncubationBaseofUrbanEnvironmentalProcessesandDigitalSimulation,CapitalNormalUniversity,Beijing100048,China)

Quantifying the dispersion of settlement spatial distribution and exploring the relationship between the distribution index with rural economic indicators,so as to provide guidance to"the whole village poverty alleviation and development plan"implementation.In this paper,with Hefeng County as the research area and administrative village as the evaluation unit,combined with the spatial exploratory analysis method,the characteristic of residential spatial distribution dispersion in Hefeng County is analyzed from the angle of humanity and nature.And using linear regression model and spatial lag regression model,the interaction between the village′s dispersion with per capita income on different natural and economic conditions is analyzed in detail.The result shows that: the dispersion evaluation results of DCI and LCI are within the scope of 0.59～4.56 and 0.14～2.61 respectively.With the higher road density,the closer distance to economic center,the smaller terrain,the dispersion index is smaller and residential space distribution is more intensive,the regional economy is more developed.In planning the layout of the village settlements,we should comprehensively consider the influence of many factors,and combine the influence of human factors such as the road.

dispersion;landscape index;the per capita net income of rural;residents;spatial distribution pattern；Hefeng County

2014-12-10；

2015-06-21

国家自然科学基金项目(40701147)；北京市自然科学基金项目(8132018)；十二五国家科技支撑计划项目(2012BAH33B03、2012BAH33B05)

杨思遥(1992-)，女，硕士研究生，研究方向为GIS方法与应用。*通讯作者E-mail：huiwangyan@sohu.com

10.3969/j.issn.1672-0504.2015.05.016

F301

A

1672-0504(2015)05-0073-06