土坝混凝土防渗墙侧壁负摩阻力分析
程素珍 杜 滨 刘莉莉
(山东省水利科学研究院,山东济南 250013)
土坝混凝土防渗墙侧壁负摩阻力分析
程素珍 杜 滨 刘莉莉
(山东省水利科学研究院,山东济南 250013)
混凝土防渗墙是土坝防渗加固比较常用的方法,但由于墙体和两侧坝体的弹性模量、强度差异较大,在上覆荷载作用下墙体与土体之间产生不均匀沉降,使防渗墙侧壁出现负摩阻力,其应力甚至达到材料的极限抗拉强度,造成墙体出现裂缝,防渗效果降低。本文以崮山水库为例,采用有限元法分析防渗墙的受力状态,探讨了模量比值k的变化对墙体负摩阻力的影响、相对沉降与负摩阻力的关系、中性点的位置等,为防渗墙的运行管理提供理论支持。
防渗墙;负摩阻力;分析
防渗墙是修筑在土石坝和松散覆盖层中起防渗作用的地下连续墙,因其防渗效果好、施工速度快、结构可靠等优点[1-2],成为山东省土石坝防渗处理的首选工程措施。但是防渗墙主要是以水泥为胶凝材料的混凝土构筑物,即使采用黏土取代普通混凝土中的大部分水泥形成的塑性混凝土浇筑防渗墙,其变形模量与坝体土也差异较大,坝体在自身沉降过程中,墙体变形小,坝体变形大,当坝体土相对墙体产生向下的位移时,土体就会对墙体产生向下的摩阻力即负摩阻力[3],当负摩阻力大于墙体材料的抗拉强度时,防渗墙就会出现开裂,裂缝的出现会严重降低墙体的防渗性能,甚至产生流土、管涌等水力破坏现象[4-5]。随墙体深度的增加,相对沉降会逐渐减小,负摩阻力逐渐消失,在墙体和其两侧的土体沉降相等处,摩阻力为零,该点即为中性点,中性点以上墙体受负摩阻力,以下受正摩阻力。因此,分析防渗墙中性点的位置、负摩阻力的大小、墙体材料的变形模量对墙体受力状态的影响等对评价防渗墙的安全状态至关重要。本文结合崮山水库大坝安全鉴定,分析了防渗墙侧壁摩阻力的变化,评价了墙体的工作状态。
1 工程概况
崮山水库位于威海市环翠区,枢纽工程由大坝、溢洪道、放水洞、电站等组成,工程规模为Ⅲ等,主要建筑物为3级。大坝系壤土心墙砂壳坝,坝顶长385m,坝顶高程28.8m,最大坝高20.3m。是一座集防洪、供水、养殖、发电等综合效益于一体的中型水库。
坝体内采用黏土心墙防渗,心墙顶高程28.10m,顶宽2m,上下游坡比为1∶0.4。心墙和坝基砂内构筑混凝土防渗墙,墙体位于坝轴线,墙长150m,厚度0.6m,上部埋入黏土心墙内, 顶高程25.00m,坝基砂内平均深度12.71m,底部嵌入基岩1.20m,墙体材料为C10素混凝土,设计轴心抗拉强度650kPa,设计轴心抗压强度5MPa,弹性模量E28=400~1000MPa;渗透系数小于1×10-7cm/s。
水库建成后不久,坝体出现了较大沉降,最大沉降量达84.5cm,且坝顶出现裂缝。水库经多年运行后,现状沉降基本稳定,但是防渗墙与墙两侧土体弹性模量差异较大,由于沉降差异,墙体侧壁易出现负摩阻力,当负摩阻力大于墙体抗拉强度时,可引起墙体裂缝。因此,采用有限单元法对防渗墙侧壁负摩阻力进行模拟计算,评价墙体的应力状态。
2 防渗墙应力分析
防渗墙应力计算采用DuncanEt-μt模型,它是一种非线性应力应变关系模型[6],两个基本变量为切线杨氏模量Et和切线体积变形模量Bt,Et、Bt表达式分别为:
式中K——模量参数;
n——无因次指数;
Pa——大气压力;
Rf——破坏比;
Kb——待定试验常数;
Bt——体积模量系数;
m——体积模量指数;
S——应力水平。
由Et、Bt作为参数进而求得土的泊松比μt为:
计算中限制Bt值在(1/3~17)Et的范围内,相当于μt在0~0.49的范围内。
坝体主要由黏土心墙、壤土坝壳、砂壳、堆石压重体和坝基砂组成,坝基基岩为片麻花岗岩,作为刚性材料考虑。坝体土计算参数均可采用常规三轴剪切试验测定[6],室内试验成果建议值见表1。防渗墙的密度、弹性模量和泊松比分别为ρd=2.4g/cm3,E=600MPa,μ=0.17。
埋于坝体和坝基中的防渗墙受力情况比较复杂,不仅受到水压力、土压力、坝体自重的影响,还由于防渗墙及其两侧的弹性模量差异较大,沉降差异引起的不均一变形产生侧壁正、负摩阻力,防渗墙底部支撑条件也是影响墙体受力的主要因素。对于已运行多年的水库,坝体变形主要是竖向变形,墙体与两侧坝体沉降差异产生的摩阻力引起的墙体竖向应力为主要内力,也是产生墙体裂缝的主要因素。
采用GEO-SIGMA/W程序进行有限元分析,计算模型、材料分布及网格划分情况见图1。防渗墙侧壁摩阻力分布见图2。
由图2可知,在心墙内部及坝基中上部的防渗墙内竖向主应力都为负值;随着深度的增加防渗墙负摩阻力逐渐减小,在深度24m处摩阻力为零,墙体和两侧土体沉降相等,定义该点为中性点,中性点向下逐渐产生了正的摩阻力。经计算墙体最大负摩阻力为1250kPa,接近墙体的极限抗拉强度值,因此,墙体内存在产生裂缝的可能。
经分析,防渗墙出现负摩阻力原因是:坝体和防渗墙的弹性模量差异较大,且墙体底部支撑条件较好,在外力作用下,墙体变形较小,而坝体材料为松散层,在自重下产生的固结沉降明显,最大沉降量达84.5cm,使防渗墙两侧的坝体沉降大于防渗墙的沉降,从而引起对墙体侧面的向下摩阻力,随着深度的增加,坝体沉降量逐渐变小,而墙体在上覆压力和负摩阻力的作用下沉降量逐渐增加,二者的相对沉降量逐渐减小,侧壁负摩阻力也逐渐减小,当相对沉降减小为零,即达到了中性点,侧壁摩阻力为零;过中性点后,上部产生的负摩阻力使防渗墙的压缩量继续增加,当大于两侧土层的变形量时,防渗墙的侧壁会出现正的摩阻力,且随着深度的增加正摩阻力在不断加大,直到防渗墙底部,其正摩阻力达到了最大值。
由于墙体底部是入岩的封闭式防渗墙,墙基坚硬,防渗墙沉降较小,而相对位移会维持较长时间,负摩阻力会长期作用于中性点以上墙体两侧。由于墙体是挡水构筑物,上下游长期存在水头差,墙体在水溶蚀等外部因素作用下,强度会逐渐降低,当负摩阻力大于材料拉应力时,会造成墙体开裂,因此,应加强墙体的长期观测。
3 不同k值下的负摩阻力计算
防渗墙侧壁产生负摩阻力的原因是墙体与两侧土体的刚度不同,在外力作用下坝体产生了相对墙体的沉降。为研究两者的刚度差异对负摩阻力的影响,选取两种材料的不同模量比值k进行计算分析,k值见表2,不同k值下的墙侧壁最大负摩阻力变化和中心点位置见图3。

表2 计算方案
注E1为防渗墙的弹性模量,E2为坝基覆盖层的模量,取E2=22kPa。
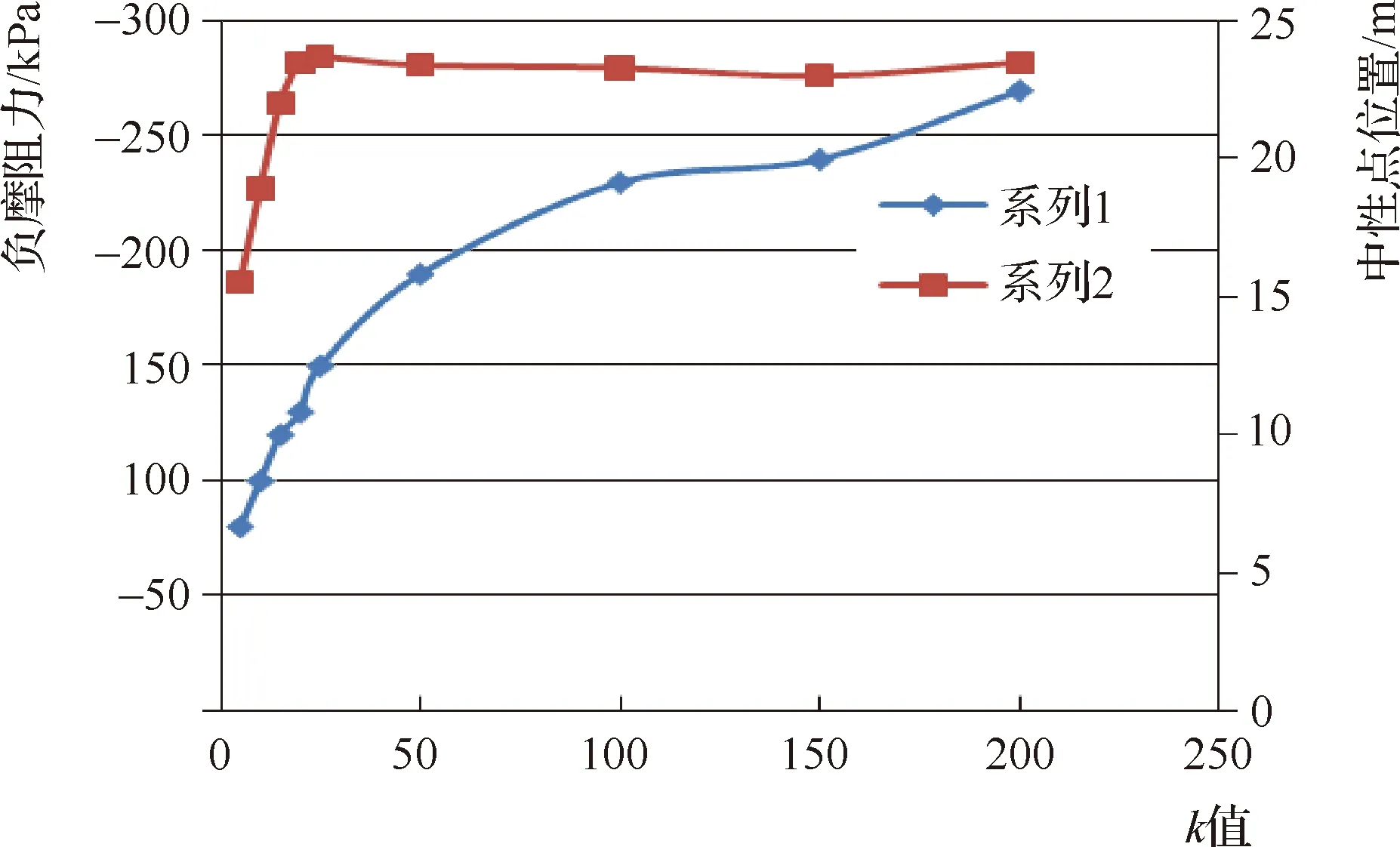
图3 k值与负摩阻力和中性点关系曲线
从图3可知,防渗墙—土体相对刚度大小对防渗墙最大侧壁摩阻力有明显的影响。随着k增大,其侧壁负摩阻力也不断加大。侧壁负摩阻力在k值较小时增长较快,但随着k值的继续增加,其最大负摩阻力的增量逐渐减小。原因是随着k值的加大,墙体的模量不断增加,在外力不变的情况下自身沉降量减小,墙体与两侧松散层的相对沉降增大,当相对位移增加到一定程度时,两侧土体产生屈服破坏,侧壁摩阻力达到峰值,此后即使再加大k值,其负摩阻力也基本保持不变。因此,为降低侧壁负摩阻力,在满足墙体抗压强度的情况下,尽量采用低弹模的塑性防渗墙。
4 k值对中性点的影响
防渗墙所受摩阻力为0的点为中性点,在墙体与两侧土体压缩模量相等时,其变形协调,在竖向应力作用下,不存在相对运动趋势,可以说处处为中性点,但是两种材料的强度总存在差异,就必然有中性点的存在。经计算防渗墙中性点位置随k值变化的情况见图3。
中性点位置在-15~23m之间,也就是在防渗墙深度的1/2~1/3处,符合端承墙的受力规律。中性点随着k值的增大而深度逐渐增加,在二者的刚度比较接近时,k值对中性点的位置影响较大,当刚度差别较大时,中性点的位置基本不随k值的变化而变化,对于崮山水库防渗墙,当k>24时,中性点的位置基本不变。原因是防渗墙的模量较小时,防渗墙的变形大,产生的相对位移小,随着深度增加,负摩阻力的增加引起的防渗墙压缩量不断变大,使防渗墙与两侧土体间的不均匀沉降得到了弥补,从而中性点位置较高。随着k值的加大,中性点下降的速度在变慢。中性点也就是墙体所受应力最大的点,因此,在工程管理中,要重点加强防渗墙底端1/3~1/2之间的施工质量,加强该处的观测。在工程设计中,防渗墙应力应变及渗压计观测设施主要安装在墙体端1/3~1/2之间,就是因为该部位受力最大,最容易出现破坏。
5 相对沉降对负摩阻力的影响分析
只要墙体与土体之间产生相对运动或有运动趋势,就会产生摩阻力,当产生滑动时摩阻力基本不变。图4为防渗墙的相对沉降量与负摩阻力的关系曲线。
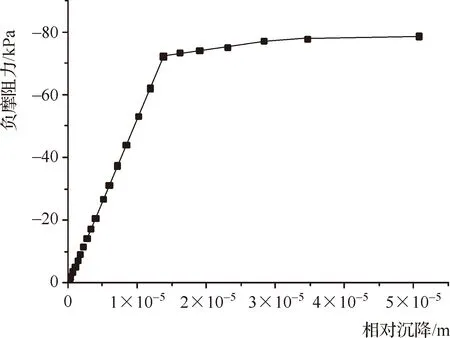
图4 防渗墙相对沉降与摩阻力的关系曲线
由图4可知,当相对沉降量小于1.5×10-5m时,负摩阻力与相对沉降量呈直线关系,说明墙体与土体之间位移在屈服范围内,当相对沉降量达到一定程度后,墙体两侧的土体产生屈服破坏,即使相对沉降值再增加,负摩阻力也不会再加大,因此,在工程中要避免屈服破坏的发生。
6 结 语
通过对崮山水库防渗墙侧壁负摩阻力和中性点位置随k值的变化规律的分析,得出以下主要结论:
a.水库经过多年运行,坝体固结沉降明显,最大沉降量达84.5cm,造成墙体产生较大的负摩阻力,其值已接近材料的极限抗拉强度,应加强墙体观测。
b.防渗墙—土体相对刚度的大小,对防渗墙最大侧壁负摩阻力有明显影响。侧壁负摩阻力在k值较小时增长较快,但随着k值继续增加,其最大负摩阻力增量逐渐减小。因此,为降低侧壁负摩阻力,在满足墙体抗压强度的情况下,尽量采用低模量的材料以适应坝体变形,从而减小防渗墙的应力。
c.防渗墙最大竖向应力的位置基本在距防渗墙底端1/3~1/2处,因此,在工程中应加强该部位的监测,防止墙体出现破坏。
[1] 郑秀培.土石坝地基混凝土防渗墙设计与计算[M].北京:水利电力出版社,1979:12-20.
[2] 苏炳煌.低弹模混凝土防渗墙新技术在村内水库除险加固工程中的应用[J].水利建设与管理,2014(7):47-50.
[3] 张展弢,冯志焱.西安黄土地区静压桩荷载沉降特性与分析[J].岩石力学与工程学报,2005,24(14):2549-2552.
[4] 杨洋,黄德强.土石坝低弹模塑性混凝土防渗墙应力变形分析[J].中国水能及电气化,2014(9):52-56.
[5] 郭亚洁.张峰水库塑性混凝土试验研究[J].水利建设与管理,2007(5):83-84.
[6] 谢定义,姚仰平,党发宁.高等土力学[M].北京:高等教育出版社,2007:111-121.
Analysis on negative friction resistance of earth dam concrete cut-off wall sidewalls
CHENG Suzhen, DU Bin, LIU Lili
(ShandongWaterConservancyScientificResearchInstitute,Ji’nan250013,China)
Concrete cut-off wall is a more commonly used method in earth dam anti-seepage reinforcement. However, elastic modulus and strength differences of walls and dam bodies on both sides are greater. Uneven settlement is produced between the walls and soil under the effect of overlying load, thereby negative friction resistance is produced on the sidewalls of cut-off wall, and the stress even can reach ultimate tensile strength of the materials, thereby leading to cracks on the walls and low seepage control effect. In the paper, Gushan Reservoir is adopted as an example. Finite element method is adopted to analyze the stress state of cut-off wall. Influence of the change of modulus ratiokto the negative friction resistance of walls, relationship between relative subsidence and negative friction resistance, position of neutral point, etc. are discussed, and theory support is provided for operation and management of cut-off wall.
cut-off wall; negative friction resistance; analysis
10.16617/j.cnki.11-5543/TK.2015.10.019
TV543+.82
A
1673-8241(2015)10-0066-05

