外爬式塔吊附着节点安全性分析

朱现磊 杨 林 张 涛

(1.中国矿业大学(北京)基建处，北京 100083； 2.中冶建筑研究总院有限公司，北京 100083)

外爬式塔吊附着节点安全性分析

朱现磊1杨 林1张 涛2

(1.中国矿业大学(北京)基建处，北京 100083； 2.中冶建筑研究总院有限公司，北京 100083)

以某高层科研楼工程项目为背景，运用有限元程序ABAQUS，模拟了不同荷载条件下外爬式塔吊附着结构的塑性损伤情况，并在极限荷载下对预埋件截面面积进行了验算分析，得出了一些有价值的结论。

外爬式塔吊，附着节点，有限元，安全性分析

0 引言

随着我国社会经济的快速发展，高层建筑大量出现[1]，在其结构施工中，塔吊是工程施工的核心设备[2]。高层建筑塔吊的科学、安全运行是确保工程施工质量、进度和安全的关键因素[3]。高层建筑动臂塔吊爬升方式分为内爬式和外爬式两种，外爬式塔吊具有塔身短、整机轻、适用性强等优点[4,5]。由于外爬式塔吊自重和外载作用于爬塔支撑架上，爬塔支撑架通过预埋件与建筑的主体结构相连[6]，因此合理的爬塔支撑架、预埋件及附着节点的受力安全性，是外爬式塔吊安全可靠工作的重要保证。

1 工程概况

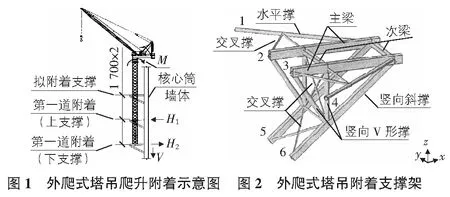
以某科研楼工程为例，根据工程特点和实际需要，施工过程中采用M760D-US型外爬附着式塔吊，塔吊通过支撑架附着于墙体上，塔架与核心筒墙体经预埋件连接。支撑架共有三道，下支撑架、上支撑架及拟附着支撑架，上支撑架和下支撑架的支座水平力平衡外爬式塔吊顶部的集中弯矩如图1所示。每个支撑架均选用Q345B钢结构材料，由主梁、次梁等结构单元组成，如图2所示。预埋件形式采用对拉钢板，锚板选用Q345钢材。锚板下混凝土强度类别为C50，轴心抗压强度设计值为19.1 MPa。本文主要对附着节点进行安全性模拟分析和计算验证。

2 节点极限荷载的有限元分析

2.1 模型建立

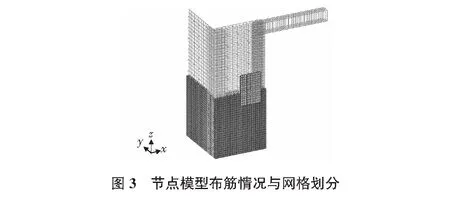
混凝土采用ABAQUS中的混凝土塑性损伤本构模型，该模型采用的是由Lubliner[7]和Lee[8]提出的混凝土塑性损伤断裂模型，以此来模拟混凝土中损伤引起的弹性刚度退化。由于模型的对称性，因此建立一半模型，节点受力考虑为极限荷载情况，梁采用弹簧单元进行简化，墙体边界耦合上弹簧单元，为柔性约束，弹簧刚度为截面法向刚度，计算式如式(1)所示。

K=∑EiAi/L(i=1，…，j)

(1)

其中，E为材料弹性模量；A为材料面积；L为结构长度；j为结构内部件数。

钢筋则采用理想弹塑性的双折线模型，三维桁架单元，钢筋和预埋件预埋部分通过ABAQUS提供的Embedded region技术耦合到混凝土部件内，各弹簧一端分别与相应的混凝土节点进行耦合，同时约束另一端位移，如图3所示。预埋件外板内侧与混凝土表面定义接触约束，法向定义为硬接触。

2.2 计算结果及分析

本文分析了模型在1倍、1.5倍、1.6倍最大外荷载条件下各部分受力、损伤以及破坏情况。不同加载条件下混凝土受力及相应混凝土结构拉伸损伤情况分别如图4，图5所示。

当加载1倍外荷载时，混凝土最大应力位于预埋件的压载部位，最大应力为10.58 MPa，核心筒墙体出现值为0.60的小范围拉伸损伤，但并未出现开裂。当荷载增加到1.5倍时，最大等效应力增加到41.56 MPa，位于核心筒墙体下部，同时拉伸裂缝继续向上下两端扩展，墙体连接位置和预埋件位置均产生了斜向裂缝，且裂缝间未见明显贯通，整个结构仍处于稳定平衡状态。当荷载继续增加至1.6倍外荷载时，核心筒土墙体斜向裂缝贯穿整个横截面，此时整个结构已经破坏，无法继续承载。

当加载1倍外荷载时，预埋件下部个别纵筋和拉筋达到屈服强度；当增加到1.5倍外荷载时，节点应力逐渐由锚筋承担，同时中部暗柱箍筋逐渐屈服，钢筋屈服位置与混凝土开裂位置基本重合，而在墙体端柱下部内侧和暗柱内侧出现局部范围压缩屈服；当加载力继续增加时，钢筋屈服范围进一步扩大，结构破坏。

3 预埋件的安全性验算

3.1 支撑架最大支座反力

通过外爬式塔吊附着节点的有限元模拟分析，得知1.5倍的外部荷载为此外爬式塔吊的极限荷载，现用1.5倍的放大系数来进行预埋件的安全性验算。

图1中，M760D-US型外爬附着式塔吊水平力H1，H2及竖向力V分别取1 080 kN，930 kN及4 350 kN，验算时假定塔吊荷载以4个均分集中力的形式作用于外爬式塔吊支撑架的支承钢梁上，即均分后的270 kN水平力作用在上支撑架，232.5 kN水平力和1 087.5 kN竖向力作用于下支撑架。

根据GB 50009—2012建筑结构荷载规范[10],计算支座反力时按承载能力极限状态设计。通过有限元分析软件MIDAS/Gen进行分析，得到支撑架最大支座反力值见表1。

表1 支撑架最大支座反力

3.2 预埋件安全性验算

根据GB 50010—2010混凝土结构设计规范[11]，该预埋件锚筋的总截面面积As≥max(A,B)，其中：

当剪力、法向拉力和弯矩共同作用时：

(2)

(3)

当剪力、法向压力和弯矩共同作用时：

(4)

(5)

(6)

ab=0.6+0.25t/d

(7)

其中,M为弯矩设计值；V为剪力设计值；N为法向拉力或压力设计值；ar为锚筋层数影响系数；ab为锚板弯曲变形折减系数；av为锚筋受剪承载力系数；t为锚板厚度，40 mm；d为锚筋直径；z为沿剪力方向最外层锚筋中心线间距；fy为锚筋的抗拉强度设计值，不大于300 N/mm2；fc为混凝土轴心抗压强度，设计值为19.1 MPa。

1)主梁节点埋腿截面面积验算。

2)水平撑处埋腿截面面积验算。

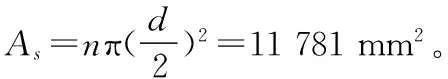
3)竖向斜撑处埋腿截面面积验算。

4 结语

以某特定工程为背景，运用数值软件ABAQUS，模拟分析不同外载条件下外爬式塔吊附着节点处的稳定性情况，并进行附着节点处预埋件截面面积理论计算，得出如下结论：

1)随着外部荷载的增大，外爬式塔吊附着节点处最大应力位置沿混凝土墙体向下移动，墙体逐渐出现裂缝，直至开裂破坏；同时，锚筋由小部分损伤变形至大部分屈服断裂，最后整个结构无法继续承载。

2)1.5倍外荷载条件下时，外爬式塔吊附着结构最大应力位于墙体下部，墙体中拉伸裂缝扩展发育，预埋件周围墙体产生斜向裂缝，此时裂缝并未完全贯穿，整个结构处于失稳边缘。

3)通过外爬式塔吊附着节点处预埋件截面面积验算可知，极限外荷载条件下，外爬式塔吊安全可靠，满足相关规范要求，为现场使用提供指导。

[1] 摩天城市网.冲向天空的1.7万亿——中国摩天城市报告[EB/OL].(2012.7.31)[2013.6.1]http//www.Motiancity.com/2012/index.php.

[2] 田金成,曹新飞,董 明.内爬式塔吊在高层建筑中的应用[J].施工技术,2009,38(10):75-77.

[3] 卿龙邦,姚 雄,肖成志，等.外爬式塔吊对高层钢板剪力墙结构影响的分析[J].华北地震科学,2013(31):24-27.

[4] 李 迪,王朝阳.超高层建筑施工中塔吊的合理应用[J].工业建筑,2012(12):79-80.

[5] 张 宇,陈晓明.爬升塔吊的外挂支承系统设计研究[J].建筑施工,2007，29(10):802-803.

[6] 曾 强.巨型桁架—核心筒结构施工技术研究与施工过程力学模拟分析[D].重庆:重庆大学,2009.

[7] Lubliner J, J.Oliver, S.Oller, et al. A Plastic-Damage Model for Concrete[J]. International Journal of Solids and Structures,1989(25):299-329.

[8] Lee J, Fenves GL. Plastic-Damage Model for Cyclic Loading of Concrete Structures[J].ASCE Journal of Engineering Mechanic,1998,124(3):892-900.

[9] ABAQUS Theory Manual, version 6.3[M].Hibbitt Karlson & Sorensen, Inc 2002.

[10] GB 50009—2012，建筑结构荷载规范[S].

[11] GB 50010—2010，混凝土结构设计规范[S].

Safety analysis of external climbing tower crane attached nodes

Zhu Xianlei1Yang Lin1Zhang Tao2

(1.ChinaUniversityofMiningandTechnology(Beijing)InfrastructureDepartment,Beijing100083,China;2.CentralResearchInstituteofBuildingandConstructionCo.,Ltd,MCCGroup,Beijing100083,China)

Based on a high-rise building project, the plastic damage of external climbing tower crane attached nodes is simulated in different load conditions using ABAQUS. Embedded parts section is checked under the condition of limit load, achieves some valuable conclusion.

external climbing tower crane, attached nodes, finite element method, safety analysis

2015-06-01

朱现磊(1983- )，男，硕士，工程师； 杨 林(1982- )，男，工程师； 张 涛(1983- )，男，硕士，工程师

1009-6825(2015)23-0025-03

TU731

A