基于单周期控制的三相三开关PFC整流器的分析与设计

王智，方炜，刘晓东

(安徽工业大学电气信息学院，安徽马鞍山243002)

基于单周期控制的三相三开关PFC整流器的分析与设计

王智，方炜，刘晓东

(安徽工业大学电气信息学院，安徽马鞍山243002)

分析研究了一种基于单周期控制的三相三开关功率因数校正(PFC)整流器。针对传统的单周期控制下输入电流平均值畸变问题，提出了一种改进的PWM调制方法，通过改变比较器的调制波信号，消除传统单周期控制方法所带来的输入平均电流中的奇次谐波，详细阐述了其工作原理和控制方法。仿真和实验结果表明，本文所提出的控制方法使得三相输入电流的谐波分量明显降低，功率因数得到显著提高。

功率因数校正;单周期控制;三相整流器

1 引言

随着电力电子技术的发展，各种整流装备，大到轧钢机用变流装置，小到荧光灯用的交流电子整流器等，均不同程度地向所连接的电网输送谐波电流，这增加了电网的损耗，尤其是大功率的整流装置带来的谐波电流更为严重。因此对高功率因数整流器的需求不断增加，而大功率三相功率因数整流器的研制更为重要。

单周期控制是一种不需要乘法器的新颖控制方法［1，2］，该技术同时具有调制和控制的双重性，其优点是无论系统处于稳态、暂态时，都能保持受控量恰好等于或正比于控制参考信号，具有控制算法简单、抗输入和输出干扰性强等优点，因而受到了越来越多的关注。目前，单周期控制主要以模拟控制为主［3，4］，而数字控制有着调试方便、可实现较复杂算法、抗噪声能力强以及可以实现远程遥控等优点，逐渐成为研究的重点，但是对数字控制的单周期PFC的研究还是主要基于单相PFC控制算法研究［5，6］。另外，传统单周期控制下输入平均电流存在畸变，文献［7］给出了解决方案，但该方案中需要实时比较调制波与载波，得到所需要的占空比信号，对于数字控制来说很难解决采样速度与实时控制之间的矛盾，因此难以实现数字控制。

本文研究了一种基于单周期控制的三相三开关PFC控制器，所采用的电路拓扑结构［8］能够有效地实现三相电路之间的解耦。基于单周期控制方法设计出的三相PFC控制器一方面可以提供较高的功率因数，另一方面，可以有效地抑制电网三相电源不对称对三相PFC控制器的影响。另外，针对传统单周期控制下输入平均电流的畸变，本文提出了一种改进的PWM调制方法，通过改变比较器的调制波信号，可有效降低传统单周期控制方法所带来的电流奇次谐波，并给出了系统的稳定性分析，为电路设计提供了理论基础。最后对本文所提的方法进行了实验验证，仿真和实验结果表明该控制方法的正确性和有效性。

2 单周期控制的工作原理及其分析

在分析单周期三相PFC的控制过程之前，先给出以下假设条件:

(1)三相电网电压对称，内阻为零;

(2)每个等效的单相三电平电路参数相同，所有开关管和二极管均为理想器件;

(3)Boost变换器工作在连续电流模式;

(4)开关管S的开关频率远大于电网电压频率，在一个开关周期(Ts)内，各相输入电压可等效为恒定值。基于单周期控制的三相三开关整流器电路结构图如图1所示。

图1 单周期控制的三相三开关整流器Fig．1 Circuits of three-phase OCC-PFC

在每个开关周期内以电网中线O点为参考点，电路工作在连续电流模式下，可以定义开关函数:

式中，ki分别对应电路的三相开关状态。由此可以得到A、B、C三点的开关周期内平均电压为:

式中，Di为开关管Si(i=a，b，c)的占空比大小;当电路达到稳态时，两电容上的电压均衡，为输出电压的一半，即Up=Un=0.5Uo，其中Up为Cp两端电压，Un为Cn两端电压。根据电感电压伏秒平衡，式(2)可简化为:

式中，Ui与ki(i=a，b，c)同号，式(3)可进一步简化为:

由式(4)可以看出三相的占空比大小只与其输入电压值及输出电压有关，与其他两相无关，从而实现了三相之间的解耦。为实现单位功率因数，变换器的各相输入特性呈纯阻性，各相输入电压、电流应满足:

式中，Re为等效输入阻抗。将式(5)代入式(4)，等式两边同乘电流采样系数Rs，则基于单周期控制下三路比较器的电感电流采样信号分别为Rsix(x=a，b，c)，计vm=0.5RsUo/Re，得:

式中，vm为电压环PI调节输出。式(6)为单周期控制的核心函数，该控制方式是一种典型的峰值电流控制方式［2，3］。下面以A相为例分析，一个开关周期内电感电流峰值ia_peak与平均值ia_avr为［7］:

式中，Uam为A相输入电压峰值，即Ua=Uamsinθ。由式(8)可以看出，单周期控制下的平均电流中存在较大的奇次谐波，主要是三次谐波，且谐波含量与开关频率和输入电感值成反比。

3 改进PWM调制的控制方案

根据第2节的分析可知，单周期控制的核心是通过实时对比比较器的调制波信号与载波信号，得到每个周期内占空比信号。但这种峰值电流调制方法会导致电感电流中存在较大的奇次谐波。为了有效改善输入电流质量，降低奇次谐波的含量，现提出一种改进的PWM调制方法。

仍以A相为例，根据单周期控制的思想，假设在一个开关周期内，初始阶段电感电流为ia_valley，电感电流的峰值为ia_peak。开关导通时，电感电流上升斜率为M1;开关关断时，电感电流的下降斜率为M2，有:

由此可以计算出一个开关周期内电感电流采样信号的平均值ua_avr为:

式中，Boost升压占空比Da=1－|Ua|/Up，Rs(ia_peak－ia_valley)=DaTsM1。

Boost电路满足0＜|Ua|/Up＜1，不难分析出当|Ua|/Up=1/3时式(12)取最小值。假设开关频率为20kHz，电感取400μH，采样系数Rs为0.1，代入式(12)得:

由式(13)可知，ia_avr与0.5(ia_peak+ia_valley)最大偏差只有1/540。因此，可近似将一个周期内的电感电流平均值等效为电感电流初始值与峰值的平均值。

基于以上分析，如果能够控制使得比较器的调制信号与载波信号的交点为电感电流初始采样值Rsia_valley和峰值采样值Rsia_peak的平均值，则ia_avr正比于Ua呈正弦变化，从而实现降低电流中各奇次谐波含量的目的。

现提出一种新的调制方法，假设新调制方式下比较器的调制波信号为u'ia，其值为每个周期电感电流初始采样值和实时绝对值采样的平均值，载波信号为1－v'm，v'm为该调制下电压环输出。单周期控制下A相PWM信号产生逻辑图如图2所示，图2中u'n_avr、u'(n+1)_avr分别表示比较器第n和n +1个周期调制波信号与载波信号的交点信号值，则:

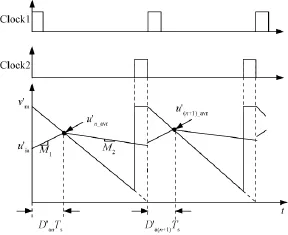
图2 A相PWM信号产生逻辑图Fig．2 Logic diagram of phase A PWM production

图2中，D'an和D'a(n+1)为新调制方式下的开关管Sa在第n和n+1个周期的占空比大小，系统稳定后，由式(6)知:

根据A相电感电压伏秒平衡(式3)，可得:

令i'a_avr=0.5(|ia_valley|+|ia_peak|)，则:

系统稳定后，式(17)中v'm、Uo为恒定值，稳态下输出等效阻抗R'e=0.5UoRs/V'm，因此:

由此，输入电流平均值Ia近似正比于输入电压Ua。与式(8)相比，式(18)中电感电流平均值已无低频奇次谐波分量，达到了提高输入电流质量的目的。

根据上述分析，改进PWM调制方式是通过改变比较器调制波信号，使其等于每个开关周期初始电流采样值与电感电流实时采样值之和，即:

式中，ia(t)为输入电感电流实时值。

改进PWM调制实现的关键在于比较器输入端电流的采样，本文设计了如图3所示的模拟控制电路，令此调制下采样系数R's=0.5Rs。

通过芯片LF398及其外围电路得到一个周期内电感电流初始采样信号uval(uval=R's|ia_valley|)，R's|ia|、uval再经过同相求和电路得到所需的比较器调制波信号u'ia。

图3 比较器输入端电流采样实现Fig．3 Realization of input current sampling of comparator

4 Simulink仿真与实验

根据前面所述的控制方法，对三相三开关PFC功率变换器进行了仿真验证，仿真参数如下:输入电压为三相对称电压，相电压有效值为220V，基波频率为50Hz，输出电压Uo=750V，开关管的工作频率为20kHz，输入滤波电感为400μH，输出电容Cp= Cn=1000μF，改进前后(采用不同的电流采样方式)电流采样系数分别为0.1和0.05，输出功率为10kW。

图4为改进前后仿真的电流波形。从波形上看，改进电流采样方式下电流正弦度更高。

为验证本文上述理论分析，设计了一台额定功率为4kW的试验样机，其相电压有效值为135V，输出电压Uo=450V，输出电容Cp=Cn=1000μF，改进前后电流采样系数分别为0.1和0.05，开关频率为20kHz，实验中选取输入滤波电感为450μH。

图5给出了基于两种不同采样方式下变换器的电流波形和输入电压波形，输入电流有效值为10A。可以看出改进后的电流波形更接近正弦波形，质能分析仪的测量结果显示改进前输入电流谐波总畸变率为6.5%，而改进后输入电流谐波总畸变率低于3.5%，各奇次谐波和THD值均明显减小。

图4 三相电流仿真波形Fig．4 Simulation waveforms of three-phase currents

图5 4kW负载时实验波形Fig．5 Experimentalwaveforms at 4kW load

图6为负载跳变时(从2.4kW到4kW)的输出电压及各相电流波形，图6中通道4为输出电压波形，其他为各相电流波形。可以看出跳变时输出电压波动较小，能够实现平稳过渡，输入电流在2～3个电网周期后就能达到新的稳态。输出功率2.4kW时THD值为6.2%左右，功率因数为0.985。

图6 负载跳变实验Fig．6 Experimentwaveforms of load step

图7为不同负载时，两种电流采样方式下变换器的输入电流THD与功率因数曲线。可以看出，改进后的PFC变换器有着更高的功率因数，更小的电流畸变(THD值更小)。

图7 两种PWM调制下电流THD与功率因数曲线Fig．7 Variation of input current THD and power factor with load in different PWM modulations

5 结论

本文设计了一种单周期控制的三相三开关PFC整流器，并提出了一种改进的PWM调制方式，理论分析了三相之间的解耦关系，抑制了电网三相电源不对称对控制器的影响。并针对采用传统控制方式下电流纹波对输入电流谐波的影响，通过改变比较器的控制输入信号，有效降低传统单周期控制方法所带来的电流奇次谐波。与传统电流采样控制方式相比，改进后的三相整流器输入奇次谐波大大减小，同时输入功率因数得到了很大提高。仿真和实验结果验证了理论分析的正确性。

［1］Xiang Deng，ZhengWei，Yi Fan，et al．Modified one cycle controlled three-phase power-factor-correction［A］．38th Annual Conference on IEEE Industrial Electronics Society［C］．2012.567-572．

［2］K M Smedeley，S Cuk．One-cycle control of switching converters［A］．IEEE Power Electronics Specialists Conference［C］．1995.1173-1180．

［3］张厚生(Zhang Housheng)．单周控制的三相三开关高功率因数整流器(Three-phase three-switch high power factor rectifierwith one cycle control)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2007，22(4):113-117．

［4］江涛，毛鹏，谢少军(Jiang Tao，Mao Peng，Xie Shaojun)．基于简单模拟控制的相VIENNA整流器研究(Study on single-phase VIENNA rectifier based on simple analog control scheme)［J］．电力电子技术(Power E-lectronics)，2009，43(11):66-68．

［5］陈兵，谢运祥，宋静娴(Chen Bing，Xie Yunxiang，Song Jingxian)．单周控制新型Buck-PFC变换器(One-cycle controlled novel Buck-PFC converter)［J］．电工技术学报(Transactions of China Electrotechnical Society)，2008，23(11):79-83．

［6］Jappe T K，Mussa SA．Current technique applied in single phase PFC Boost converter based on discrete time one cycle control［A］．2011 IEEE 33rd International Telecommunications Energy Conference(INTELEC)［C］．2011.1-5．

［7］江涛，毛鹏，谢少军(Jiang Tao，Mao Peng，Xie Shaojun)．单周期控制PFC变换器的输入电流畸变研究(Distortion issue on input current of OCC-PFC converter and its solution)［J］．中国电机工程学报(Proceedings of the CSEE)，2011，31(12):51-56．

［8］Zhang Xianjin，Fan Caihong．Research on 3-phase 4-wire VIENNA rectifier based on one cycle control［A］．2012 Fifth International Conference on Intelligent Computation Technology and Automation(ICICTA)［C］．2012.280-282．

(，cont．on p.74)(，cont．from p.56)

Design and analysis of three-phase three-sw itch power factor rectifier based on one-cycle control

WANG Zhi，FANGWei，LIU Xiao-dong
(Anhui University of Technology，Ma’anshan 243002，China)

This paper presents the analysis about three-phase power factor correction based on one-cycle control．According to the problem of the average input currents distortion under the traditional one-cycle control，an improved PWM modulation method is introduced based on the analysis．With the proposed method，the odd harmonic in input current is reduced significantly，and the paper expounds its operating principle and controlmethod．The steady-state stability analysis is explained，and the stability condition of the whole system is derived．Furthermore，the theoretical analysis is confirmed by simulation results and experimental investigations．

power factor correction;one-cycle control;three-phase rectifier

TM464

A

1003-3076(2015)01-0052-05

2013-08-11

国家自然科学基金(51207001)、安徽省自然科学基金(1308085ME66)资助项目

王智(1988-)，男，安徽籍，硕士研究生，主要从事电力电子功率变换技术的研究;方炜(1977-)，男，安徽籍，副教授，从事电力电子功率变换、非线性控制等方面的研究。