捷联惯导系统极区动基座对准

高 伟,叶 攀,石惠文,许伟通,奔粤阳

(哈尔滨工程大学自动化学院,黑龙江哈尔滨150001)

捷联惯导系统极区动基座对准

高 伟,叶 攀,石惠文,许伟通,奔粤阳

(哈尔滨工程大学自动化学院,黑龙江哈尔滨150001)

传统卡尔曼滤波对准只适用于中低纬度地区,不适用于极区。针对这一问题,提出惯性系下卡尔曼滤波对准作为极区对准方案。首先选择惯性系为对准坐标系,在惯性系内推导捷联惯导系统的速度误差方程和失准角方程,建立适用于极区对准的误差模型。以速度误差为观测量,结合误差模型建立卡尔曼滤波器并进行离散化处理。然后对该对准算法进行仿真,验证其在极区的可行性,并与传统的卡尔曼滤波对准的仿真结果进行对比。最后,分析不同速度和有加速运动等情况下该算法在极区的性能,为工程实践提供理论依据。

捷联惯导系统;极区动基座对准;惯性系;卡尔曼滤波

0 引 言

捷联惯性导航系统(strapdown inertial navigation system,SINS)是一种完全自主式、全天候的导航系统,现已被广泛应用在舰船、飞机等军事领域[12]。对于SINS来说,初始对准是SINS的关键技术之一[3-5],其精度直接影响SINS的导航精度。对于舰船SINS,目前常用的精对准方法有罗经对准和基于地理系的卡尔曼滤波对准[68]。但由于对准机理上的缺陷,这两种方法的对准精度会随纬度升高而降低,无法实现极区对准,这样舰船在极区行驶时,其导航质量在一定程度上就会受到限制。

____由于惯性技术的敏感性,国内外有关极区导航的资料较少,仅通过相关报道获知国外一些导航设备能够实现极区对准,如法国Ixsea公司[9]的SIMA30激光陀螺和俄罗斯的惯性罗经系统Vega-M,并且通过相关说明书得知SIMA30是一套基于惯性坐标系[1014]的设备。而对于我国舰艇已装备的国产惯性导航系统,其工作范围限定在南北纬70°范围内,均无法完成极区对准,也就不具备极区导航能力,这就在一定程度上限制了我国舰船的活动范围。

基于以上分析,为解决极区对准问题,本文提出惯性系下卡尔曼滤波对准作为极区对准方案。首先详细推导惯性系下SINS的误差模型,接着给出建立基于该误差模型的卡尔曼滤波器的具体步骤,进而实现惯性系卡尔曼滤波对准。通过设置不同仿真条件,分析该方法在极区对准中的适用性。

1 传统卡尔曼滤波对准的不足

传统卡尔曼滤波对准的精对准模型取在地理坐标系,

将惯性器件误差看作常值,位置信息可由GPS准确测得,

则与SINS动基座对准相关的误差方程为式中,δVE、δVN分别为载体的东向速度误差和北向速度误差;ωie为地球自转角速率;L为载体的纬度;φE、φN、φU分别为东向、北向和方位失准角;g为重力加速度;ΔE、Δ

N分别为东向和北向加速度计零偏;R为地球半径;εE、εN、εU分别为东向、北向和天向的陀螺漂移。

结合式(1),以[δVEδVN为状态量,速度为观测量,便可建立卡尔曼滤波器,进行状态估计。但是,进行状态估计并不一定都能得到状态量的精确估计值,卡尔曼滤波器还必须满足系统完全可观测的条件。经可观测度分析可知,传统对准方法建立的卡尔曼滤波器并不完全可观,其中ΔN和εE为3个不可观测量,进而导致估计误差的存在。

根据式(1),当3个不可观测量为零时,系统完全可观,求出一组失准角的估计值;当3个不可观测量不为零时,系统不完全可观,求出一组失准角的估计值,二者作差便可得失准角的估计误差[15]如下:式中分别为载体东向、北向和方位失准角的估计误差。

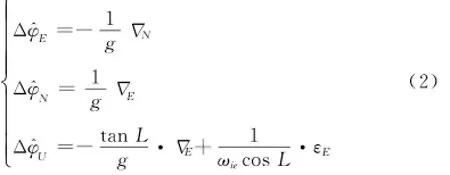
式(2)中水平失准角的估计误差为常值,与纬度无关;方位失准角的估计误差Δφ^U包括两部分,根据各参数的经验取值可知第二项起主导作用。忽略Δ^φU中第一项,对其进行仿真,其中取εE=0.01(°)/h,ωie=7.292 115 8×10-5rad/s,仿真结果如图1所示。

图1 方位失准角估计误差

2 惯性系精对准算法

上文从理论上论证了传统对准方法用于极区时的缺陷,区别于传统对准方法本文提出惯性系精对准。文中的惯性系是指地心惯性系,即坐标原点在地心,x、y轴选在赤道平面内并分别指向本初子午线和东经90°方向,z轴选在沿地球极轴指向北极的方向上。

惯性系的精对准是在粗对准的基础上进行的,惯性系粗对准结束后可得载体系至计算惯性系的转换矩阵Ci'b。设计算惯性系i'与惯性系i之间的误差角为φi,对应的误差角矩阵为Ci'i。惯性系下精对准的主要任务就是通过卡尔曼滤波得出误差角准确的估计值^φi,对准原理如图2所示。

图2 惯性系精对准原理图

估计出^φi后,姿态矩阵Cbn可表示为

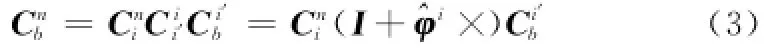
式中,^φi×为^φi的反对称矩阵;Ci'b由陀螺输出计算更新得到,其初值为粗对准结束时刻的Ci'b;Cni可由下式准确给出:式中,t为对准时间;λ、L为精对准结束时刻载体的经、纬度,由GPS准确给出。

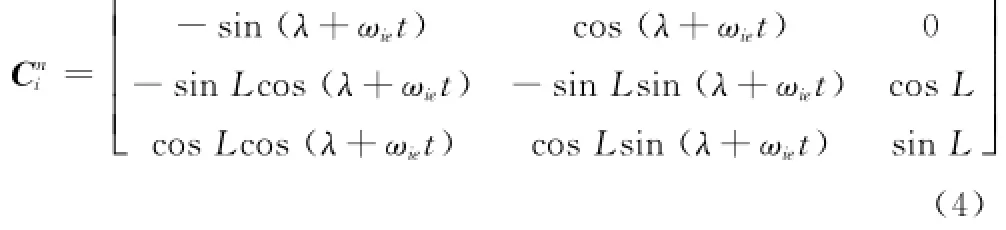
3 惯性系下SINS的误差模型

要估计惯性系下的失准角,需将误差模型建立在惯性系,推导惯性系下SINS的失准角方程和速度误差方程,建立惯性系下的卡尔曼滤波器,从而实现惯性系卡尔曼滤波对准。

3.1 失准角方程

设误差角矩阵为Ci'i,则在失准角为小角度的情况下

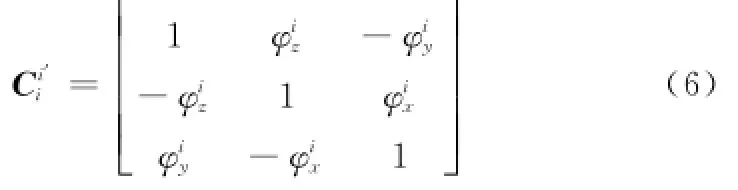
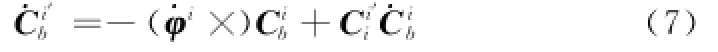
式中;φi×为失准角在惯性系上投影的反对称阵。

将式(5)代入式(7),并整理得

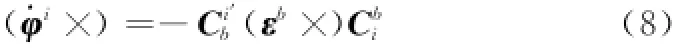
进一步展开

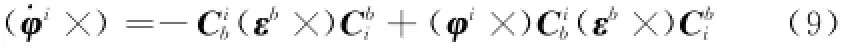
在式(9)中忽略二阶小量(φi×)C

bi(εb×)C

ib,并由矩阵的相似变换定理[16]可得失准角方程

3.2 速度误差方程

为求解速度误差方程,首先推导惯性系下SINS基本方程,设r为载体重心在惯性系内的向径,由向量的绝对变率和相对变率的关系得

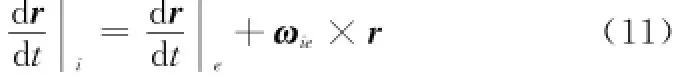
设式(11)中

式中,V为载体重心相对于地球坐标系的速度向量即地速向量。将式(12)代入式(11)中可得

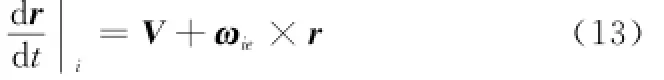
对式(13)再次求导,则

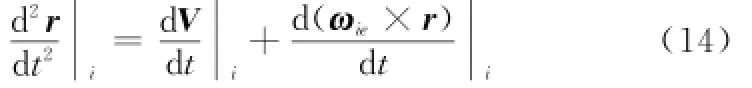
由于地球自转角速率可近似地看为常量,即

于是式(14)可写成

将式(13)代入式(16),得

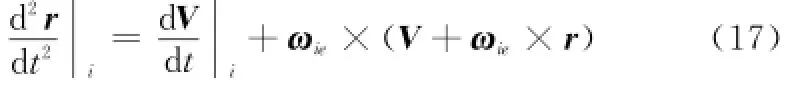
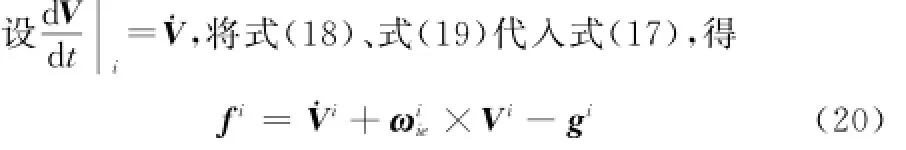
式(20)即为惯导基本方程在惯性系下的投影。式中Vi表示地速向量在惯性系下的投影；Vi表示地速在惯性系下的投影的导数;fi为加速度计输出的比力在惯性系的投影; ωiie为地球自转角速率在惯性系的投影;gi为地球重力加速度在惯性系的投影。

将式(20)投影到计算惯性系i'

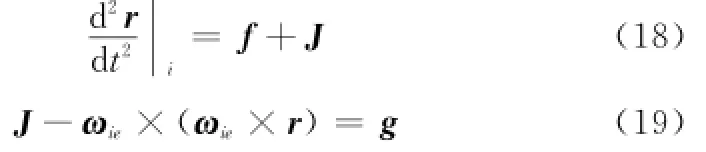
式中,f为比力输出;J为引力加速度;g为重力加速度。

由于

用式(21)减式(20)可得惯性系下动基座的速度误差方程

式中,速度误差δVi=Vi'-Vi;f～b、fb分别为加速度计输出的实际比力和理想比力;δωiie、δgi分别为计算值和理想值之差,即

在实际计算时ωiie=[0 0ωie]T可准确已知,这里取同时假设地球为规则球体即δgi=0,在忽略二阶小量的情况下式(22)化简为

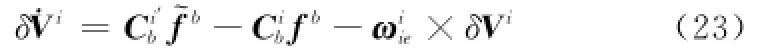
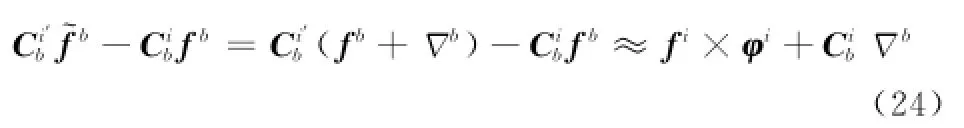
把式(24)代入式(23)得惯性系下动基座的速度误差方程

综合式(25)、式(10)可得惯性系下SINS动基座误差模型

展开上式:式中,δVx、δVy、δVx分为别惯性系x轴、y轴和z轴的速度误差;ωie为地球自转角速率;L为载体的纬度;φx、φy、φzΔ分别Δ为Δ惯性系x轴、y轴和z轴的失准角;g为重力加速度;x、y、z分别为惯性系x轴、y轴和z轴的加速度计零偏;R为地球半径;εx、εy、εz分别为惯性系x轴、y轴和z轴的陀螺漂移。

显然,与传统误差模型式(3)相比,惯性系误差模型式(27)不存在与纬度相关的tan L/R,ωiesin L,ωiecos L项。这是因为式(20)中的ωiie=[0 0ωie]T与惯导基本方程中的ωtie=相比缺少了纬度相关项,从而产生了上述差距,消除了纬度的影响,从对准机理上为实现极区对准提供了依据。

4 建立卡尔曼滤波模型

4.1 状态方程

状态方程的形式为测量,其中Vi'为惯性系下SINS解算的载体速度,Vi为GPS测得的载体在惯性系下的速度,可得惯性系下卡尔曼滤波的观测方程为

式中,X(t)为t时刻系统的状态变量;A(t)和B(t)分别为系统的状态矩阵和噪声驱动矩阵;W(t)为系统噪声序列。根据误差模型,将陀螺常值漂移和加速度计常值偏差均扩充到状态变量中,构建状态变量

状态矩阵A(t)为

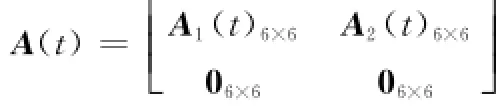
其中

A2(t)中Cij为Cib中对应的各元素,A1(t)中

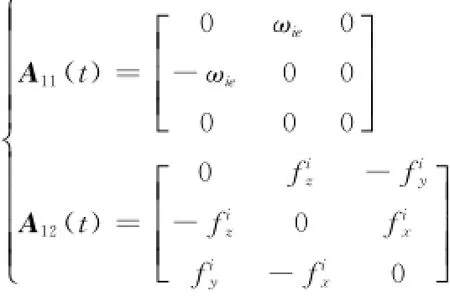
噪声驱动阵B(t)为

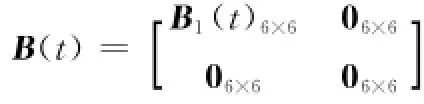
其中

噪声序列W(t)为

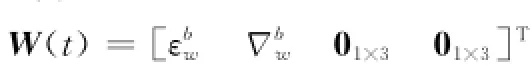
式中,εbw为载体坐标系的陀螺随机漂移,假设为Gauss白噪声过程;Δbw为载体坐标系的加速度计随机偏差,同样假设

为Gauss白噪声过程。

4.2 观测方程

取惯性系下计算地速Vi'和理想地速Vi的差值作为观

式中,Z(t)为t时刻的观测值;ηw(t)为观测噪声序列;H(t)为观测阵,其具体表达式为

5 仿真分析

由于式(28)和式(29)确定的是连续的滤波模型,要用计算机仿真还需要对模型进行离散化处理,离散化后的滤波模型[1-718]为

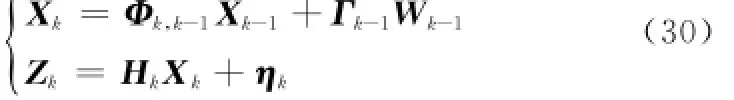
式中,Xk表示k时刻状态量的估计值;Φk,k-1表示k-1时刻至k时刻的一步转移矩阵;Γk-1表示k-1时刻的系统噪声驱动阵;Wk-1表示k-1时刻的系统激励噪声序列;Hk表示k时刻的观测阵;ηk表示k时刻的观测噪声序列。

仿真条件设置如下:

(1)陀螺的常值漂移为:εbi=0.01(°)/h(i=x,y,z);陀螺的角随机游走系数为:σε=0.001(°)/h(i=x,y,z);加Δwi速度计的常值偏置为:=1×10-4g(i=x,y,z);加速度计测量白噪声为:σΔwi=1×10-5g(i=x,y,z)。

(2)卡尔曼滤波器中P、Q、R阵初始取值如下:

(3)精对准仿真时,设置粗对准结束后水平失准角为0.1°,方位失准角为0.5°。

对于极区动基座仿真,设置舰船航行的速度为Vn= 2 m/s,Ve=2 m/s,舰船经度为126.671°,纬度分别为80°、85°、89°(极区),仿真结果如图3～图5所示。

图3 纬度为80°初始对准仿真曲线

图4 纬度为85°初始对准仿真曲线

精对准结束时两种对准方法在3种不同纬度下对应的东向误差角、北向误差角、方位误差角的稳态值如表1所示。

_表1 两种算法不同纬度对准稳态值

图5 纬度为89°初始对准仿真曲线

由图3、图4、图5和表1可知,传统对准和惯性系对准两种对准方法在纬度分别为80°、85°、89°情况下均能实现水平精对准,对准精度后者略优于前者;二者所用对准时间均在500 s左右,所以对准时间相当。在方位对准方面,惯性系对准的稳态值分别为0.205 1°、0.208 3°和0.212 1°,满足惯导系统对对准精度的要求,且随纬度变化不大;而传统对准在纬度为80°时稳态值为0.475 5°,在纬度为85°和89°时曲线最终趋于发散,无法实现对准。这是因为在极区尤其是在极点附近,舰船的运动会导致纬度的快速变化,由于传统对准方法中的方位对准受纬度影响,所以方位误差角也会随之变化,进而导致方位对准时无法达到稳态。

基于以上分析,可知传统对准无法实现极区对准,尤其是在纬度为80°～90°时对准误差较大或者无法达到稳态,这也符合图1所示失准角的变化规律。而惯性系对准的对准精度在极区基本不变,不受纬度的影响,可以实现SINS极区动基座对准。

然后,分析不同运动情况下该算法对准在极区的对准精度,设置舰船所在经度为126.671°,纬度为85°。设置以下3种情况:

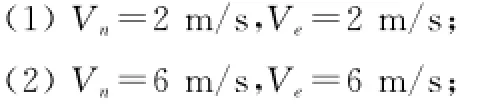
(3)初始速度Vn=2 m/s,Ve=2 m/s,舰船加速度an= 0.02 m/s2,ae=0.02 m/s2,加速时间3 min。仿真结果如图6所示。

精对准结束时舰船在3种运动形式下对应的东向误差角、北向误差角、方位误差角的稳态值如表2所示。

表2 不同运动形式情况对准稳态值

图6 不同运动情况下对准曲线

由图6和表2可知,在无加速度,速度分别为情况(1)和情况(2)两种运动形式下,前者对准的水平精度和方位精度均略高于后者。在情况(3)有加速度情况下,东向、北向的误差角与上述两者对应时刻的值为0.010 9°、-0.008 4°,虽然只是略高于其他两种情况,但由图6(a)和图6(b)可知它们有发散趋势;方位误差角虽然达到了稳态,但其对准稳态0.672 3°明显偏大。

由上述分析可知,虽然该对准方法能实现SINS极区动基座对准,但对舰船的运动形式也有一定要求,在无加速度条件下低速行驶更有利于对准精度的保障。

6 结 论

本文首先论证了纬度升高会对传统对准产生不利影响,导致传统对准方法无法实现极区对准。接着通过对SINS在惯性系内建模,实现了惯性系下卡尔曼滤波对准并将其应用于极区对准。计算机仿真结果表明,该方法能够很好地降低高纬度对对准产生的不良影响,在极区进行对准时,对准时间和对准精度两方面均能很好地满足SINS对初始对准的要求。最后,通过对不同运动形式的仿真分析,论证了无加速度低速运动为该对准方法的有利对准条件。

[1]Hays K M,Schmidt R G,Wilson W A,et al.A submarine navigator for the 21st century[C]∥Proc.of the IEEE Position Location and Navigation Symposium,2002:179-188.

[2]Qin Y Y.Inertial navigation[M].Beijing:Science Press, 2006:112-124.(秦永元.惯性导航[M].北京:科学出版社, 2006:112-124.)

[3]Silson P M G.Coarse alignment of ship’s strapdown inertial attitude reference system using velocity loci[J].IEEE Trans.on Instrumentation and Measurement,2011,12(1):1-11.

[4]Gao W X,Miao L J,Ni M L.Multiple fading factors Kalman filter for SINS static alignment application[J].Chinese Journal of Aeronautics,2011,24(2):476-483.

[5]Han S,Wang J.A novel initial alignment scheme for low-cost INS aided by GPS for land vehicle applications[J].Journal of Navigation,2010,63(4):663-680.

[6]Ali J,Ushaq M.A consistent and robust Kalman filter design for in-motion alignment of inertial navigation system[J].Measurement,2009,42(4):577-582.

[7]Qin Y Y,Zhang H Y,Wang S H.Kalman filter and integrated navigation principle[M].Xi’an:Northwestern Polyt-echnical University Press,1998:75-86.(秦永元,张洪钺,汪淑华.卡尔曼滤波与组合导航原理[M].西安:西北工业大学出版社, 1998:75-86.)

[8]Cheng X H.Moving base initial alignment research for strapdown inertial navigation system[D].Nanjing:Southeast University,1998:52-68.(程向红.捷联惯性导航系统动基座初始对准研究[D].南京:东南大学,1998:52-68.)

[9]Yan G M.Strapdown inertial navigation system moving base initial alignment and other relavant issues research[D].Xi’an: Northwest Polytechnic University,2008.(严恭敏.捷联惯导系统动基座初始对准及相关问题研究[D].西安:西北工业大学博士后研究工作报告,2008.)

[10]Gaiffe T,Cottreau Y,Faussot N,et al.Highly compact fiber optic gyrocompass for applications at depths up to 3000 meters[C]∥Proc.of the International Symposium on Under Technology, 2000:155-160.

[11]Napolitano F,Gaiffe T,Cottreau Y.PHINS:the first high performances inertial navigation system based on fiber optic gyroscopes[C]∥Proc.of the 9th Saint Petersburg International Conference on Integrated Navigation Systems,2002:296-304.

[12]Qin Y Y,Yan G M,Gu D Q,et al.Strapdown inertial navigation coarse alignment based on the swing base information[J]. Journal of Northwestern Polytechnical University,2005,23 (5):681-684.(秦永元,严恭敏,顾冬晴,等.摇摆基座上基于信息的捷联惯导粗对准研究[J].西北工业大学学报,2005,23 (5):681 684.)

[13]Yan G M.Moving base initial alignment and other related studies for strapdown inertial navigation system[D].Xi’an:Northwestern Poly technical University,2008:18 54.(严恭敏.捷联惯导系统动基座初始对准及其他相关问题研究[D].西安:西北工业大学,2008:18 54.)

[14]Yan G M,Weng J,Bai L,et al.Moving base initial alignment

and navigation and positioning based on inertial frame[J].Systems Engineering and Electronics,2011,33(3):618-621.(严恭敏,翁浚,白亮,等.基于惯性参考系的动基座初始对准与定位导航[J].系统工程与电子技术,2011,33(3):618 -621.)

[15]Zhang Y.Research of alignment technology for ship’s strapdown inertial navigation system[D].Harbin:Harbin Engineering University,2012.(张义.舰船捷联惯性系统初始对准技术研究[D].哈尔滨:哈尔滨工程大学,2012.)

[16]Gao W,Ben Y Y,Zhang X,et al.Rapid fine strapdown INS alignment method under marine mooring condition[J].IEEE Trans.on Aerospace and Electronic Systems,2011,47(4):2887 -2893.

[17]Choukroun D,Bar-Itzhack I Y,Oshman Y.A novel quaternion Kalman filter[J].IEEE Trans.on Aerospace and Electronic Systems,2006,42(1):174-190.

[18]Subramanian V,Burks T F,Dixon W E.Sensor fusion using fuzzy logic enhanced Kalman filter for autonomous vehicle guidance in citrus groves[J].Transactions of the ASABE,2009,

52(5):1411-1422.

Polar moving base alignment for strapdown inertial navigation system

GAO Wei,YE Pan,SHI Hui-wen,XU Wei-tong,BEN Yue-yang
(Automation College,Harbin Engineering University,Harbin 150001,China)

The traditional alignment method with Kalman filter is available in the low and middle latitude region,but not available in the polar region.For this issue,we propose the Kalman filter alignment under inertial frame as a solution.Firstly,the inertial frame is chosen to play the role of the alignment frame.The error model of a strapdown inertial navigation system which is applicable to the polar region alignment is derived under the inertial frame.And the misalignment angle equation and the velocity error equation are included in the error model of the navigation system.In this paper,the velocity error is used as the measurement information and the discrete Kalman filter is obtained on the basis of the alignment error model.Secondly,simulations are implemented to evaluate the feasibility of the proposed alignment algorithm in polar regions,compared with the traditional alignment method with Kalman filter.Moreover,the performances of the proposed algorithm under different speeds and accelerations are specially analyzed in order to provide theoretical basis for practical applications.

strapdown inertial navigation system;polar moving base alignment;inertial frame;Kalman filter

U 666.1

A

10.3969/j.issn.1001-506X.2015.03.24

高 伟(1977-),男,教授,博士,主要研究方向为捷联导航技术、光学陀螺技术、惯性测量技术、海洋运载器综合导航技术。

E-mail:gaow@hrbeu.edu.cn

叶 攀(1990-),男,硕士研究生,主要研究方向为捷联导航初始对准算法。

E-mail:yepan500577@sina.com

石惠文(1991-),男,主要研究方向为惯性导航初始对准技术。

E-mail:1394708027@qq.com

许伟通(1990-),男,硕士研究生,主要研究方向为捷联导航系统算法。

E-mail:252816821@qq.com

奔粤阳(1981),男,副教授,博士,主要研究方向为捷联惯性导航系统方案与系统算法、多传感器信息融合技术。

E-mail:byy@hrbeu.edu.cn

网址:www.sys-ele.com

1001-506X(2015)03-0626-07

2014 03 21;

2014 06 11;网络优先出版日期:2014 09 24。

网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20140924.0938.004.html

国家自然科学基金(51379042);中央高校基本科研业务费专项资金(heucf041420)资助课题