低轨回归轨道卫星轨迹漂移特性分析与控制
温生林,闫 野,张 华
(1.国防科学技术大学航天科学与工程学院,湖南长沙410073; 2.北京航天控制中心,北京100094)
低轨回归轨道卫星轨迹漂移特性分析与控制
温生林1,闫 野1,张 华2
(1.国防科学技术大学航天科学与工程学院,湖南长沙410073; 2.北京航天控制中心,北京100094)
针对低轨回归轨道卫星,建立了星下点轨迹漂移的数学模型,研究了星下点轨迹保持控制的问题。首先,分析了回归轨道星下点轨迹的约束条件,给出了星下点轨迹漂移与卫星轨道根数偏差之间的关系。在此基础上,将星下点轨迹保持控制问题转化为基于平均轨道根数的相对轨道控制问题,其中参考卫星是虚拟的,仅受到地球引力影响,利用高斯摄动方程建立了包含J2摄动和大气阻力摄动的相对运动方程,基于Lyapunov理论设计了星下点轨迹保持的相对平均轨道根数反馈控制律。仿真结果表明,所设计的星下点轨迹控制律能有效地实现星下点轨迹保持的要求。
低轨回归轨道;轨迹漂移;轨迹保持;平均轨道根数;高斯摄动方程
0 引 言
回归轨道是指星下点轨迹经过一段时间后重复出现的轨道[1]。我国的神州系列载人飞船、环境减灾卫星星座[2]以及国外的LANDSAT、SPOT、ENVISAT、RADARSAT等均采用回归轨道。回归轨道的主要优点在于:在一个固定的周期内,卫星的星下点轨迹会重复经过该地区,满足对特定地面目标周期性观测的任务需求,也便于卫星测控任务的实施。低轨回归轨道卫星在轨运行期间,由于受到大气阻力的衰减影响,使得轨道半长轴逐渐变小,轨道周期变短,导致星下点轨迹偏离参考轨迹向东发生漂移,从而破坏了星下点轨迹回归所需要的轨道参数条件。为此,需要研究星下点轨迹漂移的控制策略,使得星下点轨迹保持在参考轨迹附近。
目前为止,已有一些学者针对低轨卫星星下点轨迹保持问题展开了研究。文献[3]采用限制星下点轨迹漂移范围的方式,研究了航天器的轨道维持方法。文献[4]分析了大气阻力摄动引起的星下点轨迹漂移特性,研究了基于轨道半长轴偏置的星下点轨迹保持方法,该方法能有效地将星下点轨迹漂移控制在允许的范围内。文献[5]分析了太阳同步轨道卫星降交地方时产生漂移的原因,研究了大气阻力和太阳引力摄动对将交点地方时的影响,采用轨道参数偏置法设计了卫星将交点地方时漂移控制策略。文献[6]研究了低轨回归连续覆盖轨道的特性,分析了大气阻力引起的轨道衰减对星下点轨迹的影响,设计了基于速度脉冲的星下点轨迹保持方法。文献[7]研究了轨道半长轴衰减和轨道倾角长期变化引起的星下点轨迹漂移,给出了增大半长轴偏置量的星下点轨迹保持方法和计算模型。文献[3-7]都只考虑轨道半长轴或轨道倾角的变化对星下点轨迹漂移的影响,采用轨道半长轴或倾角偏置法设计了星下点轨迹保持的控制策略,未全面考虑其他轨道根数变化对星下点轨迹漂移的影响。
为了更好地描述星下点轨迹相对于参考轨迹的变化,本文通过引入参考卫星,分析了卫星轨道根数偏差对星下点轨迹漂移的影响,研究了星下点轨迹保持控制问题。首先,分析了回归轨道星下点轨迹的约束条件,研究了星下点轨迹漂移距离与星下点位置偏差的关系,考虑到卫星轨道控制是在惯性空间实施的,研究了星下点地理位置偏差与相对轨道根数偏差之间的关系。其次,将星下点轨迹保持问题转化为基于平均轨道根数的相对轨道保持控制问题,设计了星下点轨迹保持的控制律,对星下点轨迹保持的仿真结果表明,所设计的轨迹控制律是有效的。
1 回归轨道与星下点轨迹
1.1 回归轨道的约束条件
回归轨道卫星的轨道特性是星下点轨迹周期性重复,即经过一段时间后,星下点又重新通过原先经过的路线。星下点轨迹是卫星位置向量与地球表面交点在地球表面的运动轨迹,是卫星轨道运动和地球自转运动的合成,星下点位置一般用地理经度和纬度表示。卫星连续两次在上升段(或下降段)经过赤道面时,相邻的轨迹在赤道上的经度差ΔλAN可表示为

式中,ωE为地球自转角速度;Ω为轨道升交点的长期变化率;TΩ为轨道交点周期。
交点周期是卫星在轨道上连续两次在上升段(或下降段)经过赤道面的时间间隔。仅考虑J2摄动时,交点周期TΩ的计算公式[8]为
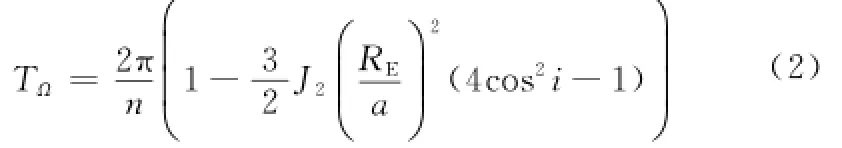
式中,n为轨道平均角速度;RE为地球半径;a为轨道半长轴;i为轨道倾角。
若设计合适的轨道半长轴、倾角和偏心率,使得卫星在d天内运行k圈后星下点轨迹重复一次,此时回归周期为d天,回归轨道的条件满足:

仅考虑J2摄动项,回归轨道的轨道半长轴a、轨道倾角i的约束方程如下:
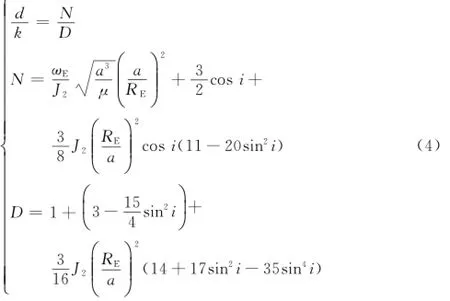
式中,μ为地球引力常数。
1.2 星下点轨迹漂移数学模型
卫星在轨运行期间受地球非球形引力、大气阻力等摄动力的影响,实际运行轨道逐渐偏离标称的设计轨道,导致卫星实际的星下点轨迹偏离标称轨迹,从而影响到地面轨迹的回归特性。
为了描述星下点轨迹的漂移,引入参考卫星和参考卫星星下点坐标系。参考卫星是虚拟的,仅受地球引力的作用。参考卫星星下点坐标系(SR-xRyRzR),如图1所示,原点位于参考卫星的星下点SR,星下点位置SR在地固坐标系中表示为地理经度、纬度(λR,φR),SRxR轴位于当地地平面内,沿当地纬度圈指向正东,SRyR轴位于当地地平面内,沿当地子午圈指向正北。
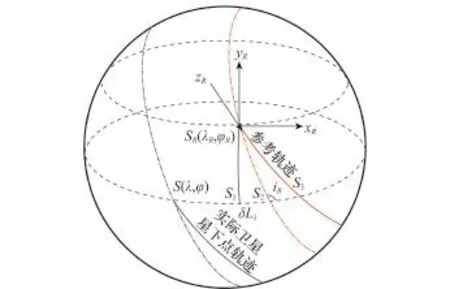
图1 星下点轨迹漂移示意图
定义星下点轨迹漂移角位移δLλ为给定纬度处实际卫星星下点轨迹与参考轨迹地理经度的偏差。一般将赤道面的星下点轨迹漂移δLAN来衡量星下点轨迹的漂移程度[9]。如图1所示,若t时刻,实际卫星的星下点位置S为(λ,φ), S1为参考卫星星下点所在的子午圈与实际卫星星下点处的纬线圈的交点,S2为实际卫星星下点处的纬线圈和参考轨道平面在地球表面投影的交点,S3为纬度φ处参考卫星的星下点。实际卫星星下点S和参考卫星星下点SR的地理经度差δλ=λ-λR,纬度差δφ=φ-φR,在图1中分别用表示。在球面直角三角形ΔSRS1S2中,在小角
度假设下,可得
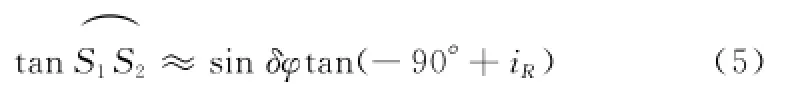
式中,iR表示参考卫星的轨道倾角。
由式(5)可得
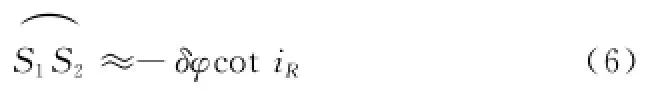
纬度φ处实际卫星星下点相对于参考卫星星下点S3的西退速率为cosφ(ωEΩR),故
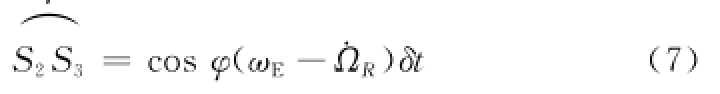
式中;ΩR表示参考卫星轨道升交点赤径的长期变化率;δt表示参考卫星从纬度φ飞行至φR的时间间隔。
由图1可知:纬度φ处星下点轨迹漂移δLλ是星下点地理经度偏差S1S、地理纬度偏差δφ引起的轨迹漂移S1S2以及实际星下点S相对S3点的西退角位移三者共同作用的结果,结合上述分析过程,可将δLλ表示为

时间间隔δt可表示为

根据纬度幅角、轨道倾角和地理纬度的关系式sinφ= sin u sin i,可得
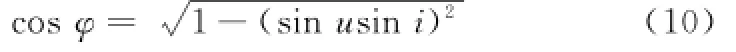
将式(9)和式(10)代入式(8),可得
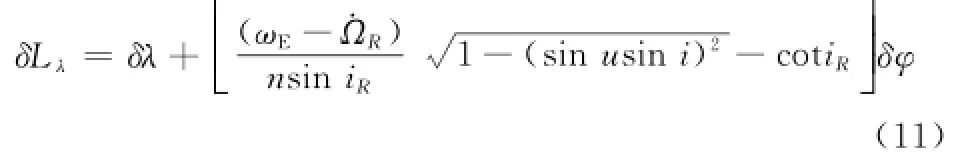
式(11)建立了星下点轨迹漂移距离与实际卫星星下点地理位置偏差的关系,但是卫星轨道控制是在惯性空间中实施的,因此需要研究实际卫星星下点地理位置偏差与卫星轨道根数偏差之间的关系。
定义卫星的平均轨道根数向量为
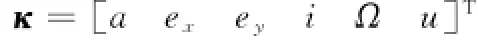
式中,ex=e cosω;ey=e sinω;e为偏心率;ω为近地点幅角。
两台手扶拖拉机突突突地上路了,我骑车跟在后面,就见眼前一股股黑烟飘进了夜的深处。我落在了后面,出村后停下来回望了一下柳家营的灯光,就觉得这里是一个神秘的村落。
定义实际卫星与参考卫星(下标R)的相对平均轨道根数向量为
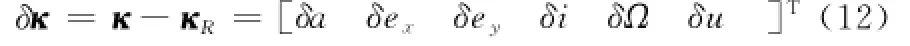
定义参考卫星的轨道坐标系ORRTN:OR为参考卫星质心,ORR轴为径向轴,沿卫星径向方向为正;ORT轴在参考卫星轨道平面,与ORR轴垂直,指向卫星运动方向;ORN轴由参考卫星质心出发,沿轨道面法向为正。设参考卫星在惯性空间的位置向量为rR,实际卫星相对参考卫星的位置向量为δr,在参考卫星轨道坐标系中表示为[x y z]T。在一阶近似下可得相对位置向量与相对平均轨道根数之间[10]的关系

式中
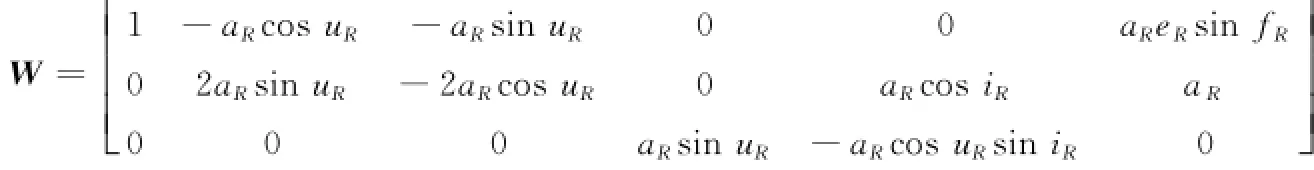
参考卫星轨道坐标系与参考卫星星下点坐标系的转动次序为:将参考卫星轨道坐标系先绕ORR轴转-iR角,再绕SRxR轴转90°,最后绕SRzR轴转90°。易知此时的坐标转换矩阵为
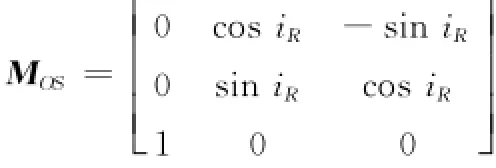
相对位置向量δr和星下点位置偏差δλ、δφ的关系为

利用式(11)、式(13)和式(14)星下点轨迹漂移的相对平均轨道根数表示为
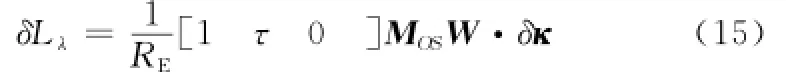
式(15)表明:星下点轨迹漂移δLλ是相对平均轨道根数向量、纬度幅角u和轨道倾角i的函数。当u=0时,可得升交点处的星下点轨迹漂移δLAN为
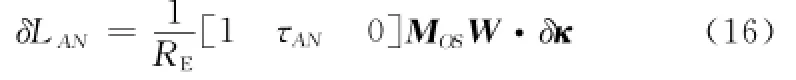
显然,升交点处的星下点轨迹漂移仅是相对平均轨道根数的函数。
2 相对运动动力学方程
2.1 基于平均轨道根数的高斯摄动方程
瞬时轨道根数随时间的变化规律可由高斯摄动方程来描述,高斯摄动方程的矩阵形式[11]可表示为

式中,κosc为瞬时轨道根数向量;向量A(κosc)描述了自由飞行条件下瞬时轨道根数的变化;B(κosc)为控制影响矩阵;u为控制加速度向量,u=[uruθuh]T。
从瞬时轨道根数向量κosc到平均轨道根数向量κ的解析变换[12]可表示如下:

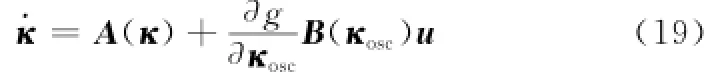
根据瞬时轨道根数和平均轨道根数的变换理论和方程式(17),可得平均运动的高斯摄动方程为式中,矩阵的非对角元素与J2项的量级相当或者更小,可以近似为一个6×6的单位矩阵13。由于瞬时轨道根数和平均轨道根数的差值与J2摄动相比很小,用瞬时轨道根数或平均轨道根数计算矩阵B的数值差很小,因此可假设矩阵B是根据平均轨道根数计算得到的,即有

对于低轨道卫星,地球非球形J2摄动和大气阻力摄动是主要摄动力。考虑地球引力和大气阻力摄动的平均轨道根数向量的高斯摄动方程为[1415]

式中,向量Ag(κ)和Adrag(κ)分别描述了在地球引力和大气阻力摄动作用下平均轨道根数的变化情况。
下面给出向量Ag(κ)、Adrag(κ)和矩阵B(κ)的具体表达式。
(1)向量Ag(κ)
考虑J2摄动影响后,向量Ag(κ)的表达式为
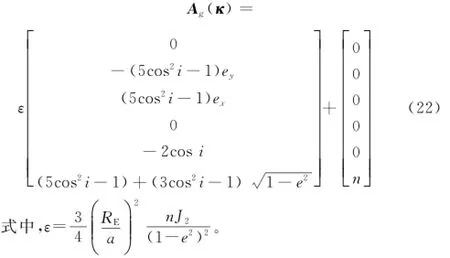
(
2)向量Adrag(κ)
卫星所受的大气阻力加速度为
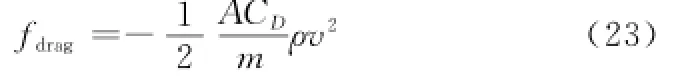
式中,A为迎风面积;CD为大气阻力系数;m为卫星质量;ρ为卫星所在位置的大气密度;v为卫星的飞行速度。
向量Adrag(κ)的表达式为

(3)矩阵B(κ)

2.2 相对平均轨道根数动力学方程
参考卫星仅受到地球引力的作用,其平均轨道根数的高斯摄动方程为

式(21)减去式(26)可得

将Ag(κ)和Adrag(κ)分别在κ=κR处线性化,有
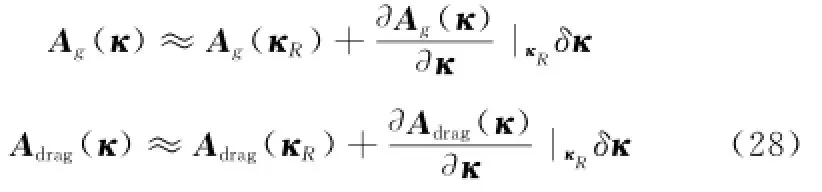
将式(28)代入式(27),可得基于相对平均轨道根数的动力学方程为
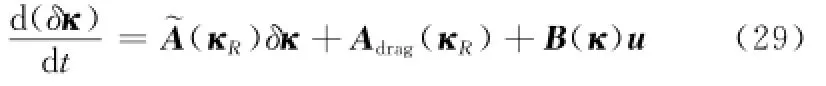
式中,~A(κR)为动力学方程的雅可比矩阵,~A(κR)可表示为
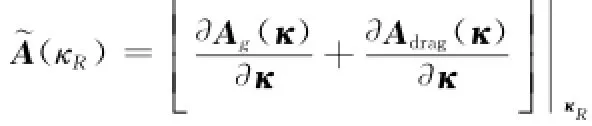
3 星下点轨迹保持的控制器设计
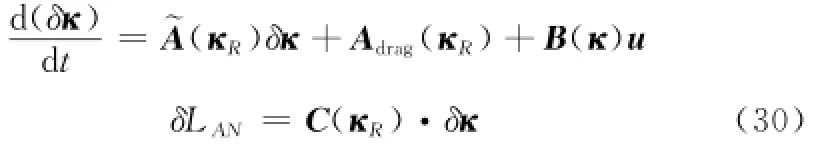
在进行卫星星下点轨迹保持的控制过程中,假定卫星的位置和速度是可以测量的,且大气密度可通过大气模型建模得到。则星下点轨迹保持的控制问题可描述为:在星下点轨迹存在漂移的情况下,设计控制加速度向量u(t),在控制加速度作用下,使得星下点轨迹由初始的偏离参考轨迹状态保持到参考卫星的星下点轨迹上。
根据式(16),结合相对平均轨道根数的动力学方程式(29),可得星下点轨迹漂移控制的数学模型
式(30)中,Adrag(κR)表示参考卫星受到的大气阻力对相对平均轨道根数的影响。下面基于Lyapunov理论来设计星下点轨迹漂移的控制律,定义Lyapunov函数为升交点处的星下点轨迹漂移δLAN的正定量
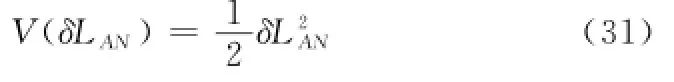
对V求导,并将式(30)代入,得到
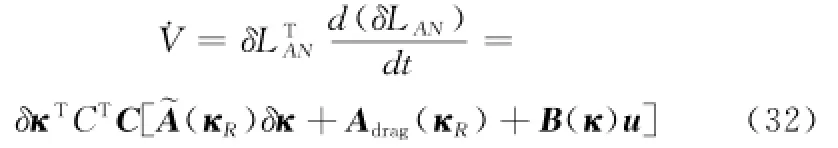
规定V是负定量

式中,P为正定反馈增益矩阵。
基于Lyapunov意义下稳定的闭环相对平均轨道根数变化的动力学控制约束如下:

值得注意的是,式(34)中P并不一定是常值矩阵,在设计所需的正定反馈增益矩阵P时,需要再次用到相对平均轨道根数的高斯摄动方程。比如,分析式(29)中的控制增益矩阵B(κ),很容易知道最好在卫星穿越赤道区域时调整轨道倾角。当u=0°,180°时,δi的反馈增益应较大一些;当u=±90°时,δi的反馈增益应较小一些。当相应轨道根数的控制效率最大时,时变的反馈增益取最大值;控制效率最低时,反馈增益取最小值或者零。根据B(κ)的表达式,可以选择反馈增益矩阵P为对角矩阵,对角线上的元素[16]如下:
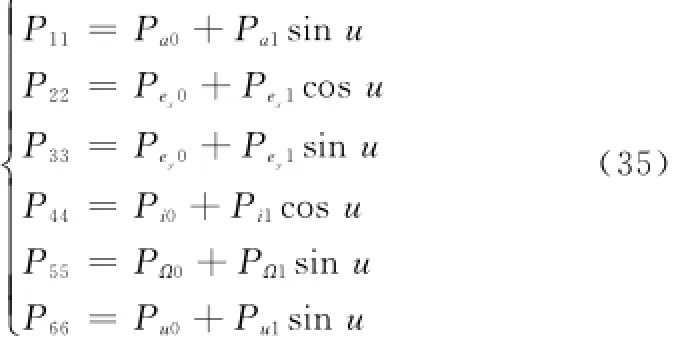
式中,Pj0和Pj1均为常数(j表示轨道根数),且Pjj>0。
由于控制加速度向量只有3个分量,而这里又期望能控制6个轨道根数,因此控制约束方程组是超定的,采用最小二乘逆求解u,可得
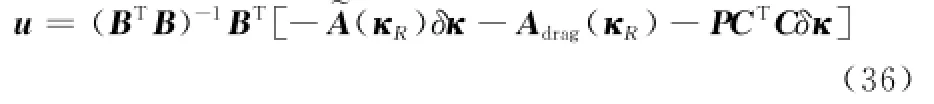
4 算例仿真及结果分析
本节以某一低轨近圆回归轨道卫星为例,通过算例验证本文提出的星下点轨迹漂移控制策略的有效性。
对于低轨近圆轨道,若星下点轨迹的回归条件为3天飞行47圈,轨道倾角为45°时,由回归轨道约束方程(4)计算的回归轨道半长轴为6 677.292 km,轨道高度为299.155 km。初始时刻实际卫星和参考卫星的平均轨道根数见表1。实际卫星受到地球引力和大气阻力的作用,参考卫星仅受到地球引力的作用。实际卫星的大气阻力系数为2.2,面质比为0.02,按照CIRA大气模型,在太阳活动平年(F10.7=150)计算出轨道高度为299.155 km处的大气密度为1.983×10-11kg/m3。

_______表1_初始时刻参考卫星和实际卫星的平均轨道根数
对于低轨卫星,大气阻力引起的轨道半长轴衰减是导致星下点轨迹漂移的最主要因素。自由飞行条件下轨道半长轴和星下点轨迹漂移δLAN的变化见图2和图3。结合图2和图3,初始时刻相对轨道半长轴δa为5.845 km,星下点轨迹漂移REδLAN为21.75 km,实际卫星位于参考卫星的东侧。考虑到δa>0,卫星星下点轨迹向西漂移,在大气阻力作用下半长轴逐渐减小,直到约105s后,δa=0,半长轴a=aR,此时星下点轨迹漂移至最西端-12.68 km处,此后轨道半长轴继续减小,但由于δa<0,星下点轨迹转而向东漂移,逐渐远离参考卫星的星下点轨迹。
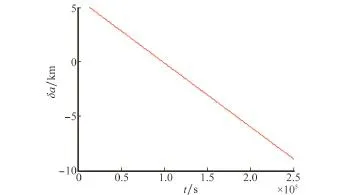
图2 自由飞行条件下相对轨道半长轴的变化
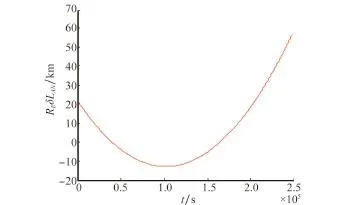
图3 自由飞行条件下星下点轨迹漂移的变化
为了使卫星星下点轨迹保持在参考轨迹附近,必须进行轨道控制。反馈增益矩阵P中的相关参数取值如下:Pa0= 0.5×10-3,Pa1=0;Pex0=1×10-3,Pex1=1×10-4;Pey0=1× 10-3,Pey1=1×10-4;Pi0=1×10-3,Pi1=0.5×10-3;PΩ0= 1×10-3,PΩ1=0.5×10-3;Pu0=1×10-3,Pu1=0。基于Lyapunov理论的星下点轨迹漂移控制的仿真结果如图4~图6所示。
图4给出了星下点轨迹漂移的变化曲线。由图4可得:星下点轨迹漂移REδLAN在4 110 s内由初值21.75 km减小至-12.84 km,随后逐渐振荡增加,约4×104s内收敛至0。图4表明,在大气阻力摄动和卫星地面轨迹存在初始偏移条件下,基于Lyapunov理论的星下点轨迹控制方法能够使得卫星星下点轨迹保持到参考轨迹上,验证了控制方法的有效性。
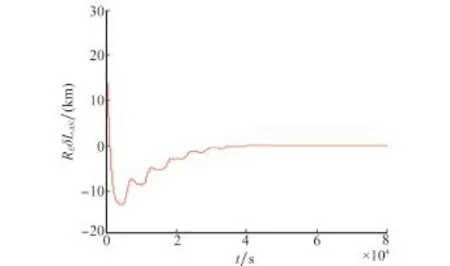
图4 星下点轨迹漂移变化曲线
图5给出了相对平均轨道根数变化曲线。由图5可得:轨道半长轴偏差δa由初值5.845 km逐渐减小,约1× 104s后减小至0。偏心率矢量偏差δex在1.5×103s内由初值5×10-4增加至峰值0.010 3;随后振荡减小,约1.741 ×104s后减小至-2.329×10-3;然后逐渐振荡增加,约7 ×104s后收敛至0。δey由初值1.57×10-4逐渐增加,约2.5×103s后增加至峰值0.015 43,随后振荡减小,约6× 104s后收敛至0。轨道倾角偏差δi由初值0.5°振荡衰减,约4×104s后收敛至0。升交点赤径偏差δΩ在初始8× 103s内由初值-1.5°增加至0.015°,随后保持小幅振荡,约4×104s后收敛至0。纬度幅角偏差δu由初值4°逐渐减小,约4×103s后减小至-0.111 5°,随后振荡衰减,约3.5 ×104s后收敛至0。

图5 相对平均轨道根数变化曲线
图6给出了控制加速度随时间的变化曲线。由图6可得:径向加速度ur由初值0.145 m/s2逐渐减小,约6×103s后减小至-0.02 m/s2,随后振荡衰减,约4×104s后收敛至0。横向加速度uθ由初值-1.65×10-3m/s2逐渐增加,约1.5×104s后增加至3.33×10-5m/s2,随后保持不变。法向加速度uh由初值0.171 m/s2逐渐减小,约2 000 s后减小至-0.004 23 m/s2,随后振荡衰减,约4×104s后收敛至0。

图6 控制加速度变化曲线
5 结 论
低轨回归轨道卫星由于其星下点轨迹周期性重复的特性能很好地满足相关任务需求,因此研究低轨回归轨道卫星的星下点轨迹漂移特性与控制具有重要的理论意义和工程意义。本文针对低轨回归轨道卫星,研究了其星下点轨迹满足回归条件的轨道约束,分析了影响星下点轨迹漂移的主要因素,建立了星下点轨迹漂移的数学模型,将星下点轨迹漂移的控制问题转化为卫星编队的相对轨道保持问题,基于Lyapunov控制理论设计了星下点轨迹保持的相对平均轨道根数反馈控制律。仿真结果表明,此方法满足星下点轨迹保持要求。本文的研究结果也可为太阳同步轨道、太阳同步回归轨道等涉及星下点轨迹保持需求的轨道控制问题提供技术参考。
[1]Yang J C.Spacecraft orbital dynamic and control[M].Beijing: China Astronautic Publishing,2005:196-198.(杨嘉墀.航天器轨道动力学与控制(1)[M].北京:中国宇航出版社,2005:196 -198.)
[2]Liu L F,Wang X L,Bai Z G,et al.Orbit maintenance technology and implement for HJ-1A/B constellation[J].Chinese Space Science and Technology,2012,29(5):69-75.(刘龙飞,王兴玲,白照广,等.环境减灾A、B星星座轨道维持技术与实践[J].中国空间科学技术,2012,29(5):69-75.)
[3]Cui H Y,She M S.An orbital maintenance method of spacecraft[J]. Spacecraft Engineering,1995,4(4):21-33.(崔海英,佘明生.航天器的一种轨道维持方法[J].航天器工程,1995,4(4):21-33.)
[4]Aorpimai M,Palmer P L.Repeat-groundtrack orbit acquisition and maintenance for earth-observation satellites[J].Journal of Guidance,Control,and Dynamics,2007,30(3):654-659.
[5]Yang Y A,Feng Z R,Sun L Y,et al.Shift control method for the local time at descending node based on sun-synchronous orbit satellite[J].Journal of Systems Engineering and Electronics, 2009,20(1):141-145.
[6]Fu X F,Wu M P,Tang Y.Design and maintenance of low-earth repeat groundtrack successive-coverage orbits[J].Journal of Guidance,Control,and Dynamics,2012,35(2):686-691.
[7]Cui P,Fu Z Q.Optimal research on satellite track keeping strategy for low earth orbit satellite[J].Electronic Measurement Technology,2013,36(8):41-44.(崔鹏,傅忠谦.LEO卫星星下点轨迹保持策略优化研究[J].电子测量技术,2013,36(8):41-44.)
[8]Vtipil S D,Newman B.Determining an earth observation repeat groundtrack orbit for an optimization methodology[J].Journal of Spacecraft and Rockets,2012,49(1):157 164.
[9]De Florio S.Precise autonomous orbit control in low earth orbit: from design to flight validation[D].Glasgow:University of Glasgow,2013:36-40.
[10]Schaub H.Relative orbit geometry through classical orbit element differences[J].Journal of Guidance,Control,and Dynamics,2004,27(5):839-848.
[11]Tavakoli M M,Assadian N.Model predictive orbit control of a low earth orbit satellite using Gauss’s variational equations[J]. Journal of Aerospace Engineering,doi:10.1177/0954410013516252.
[12]Brouwer D.Solution of the problem of artificial satellite theory without drag[J].The Astronomical Journal,1959,64(1274): 378-397.
[13]Schaub H,Vadali S R,Alfriend K T.Spacecraft formation flying control using mean orbit elements[J].Journal of the Astronautical Sciences,2000,48(1):69-87.
[14]De Florio S,D’Amico S.Optimal autonomous orbit control of remote sensing spacecraft[C]∥Proc.of the 19th AIAA/AAS Space Flight Mechanics Meeting,2009.
[15]De Florio S,D’Amico S,Radice G.Precise autonomous orbit control in low earth orbit[C]∥Proc.of the AIAA/AAS Astrodynamics Specialist Conference,2012.
[16]Schaub H,Junkins J L.Analytical mechanics of aerospace systems[M].AIAA education series,American Institute of Aeronautics and Astronautics,2003:532- 537.
Analysis and control of groundtrack drift for recursive low earth orbit satellites
WEN Sheng-lin1,YAN Ye1,ZHANG Hua2
(1.College of Aerospace Science and Engineering,National University of Defense Technology, Changsha 410073,China;2.Beijing Aerospace Control Center,Beijing 100094,China)
For recursive low earth orbit satellites,the groundtrack drift model is formulated and the control problem of groundtrack maintenance is investigated.Firstly,the restriction condition for recursive groundtrack is analyzed and the relationship between groundtrack drift and satellite orbital element deviation is given.Then, the groundtrack maintenance control problem is transformed to a relative orbit control problem using mean orbit elements,in which the reference satellite is virtual and only affected by gravitational orbit perturbation.The relative motion is modeled by Gauss’s variational equations including J2and drag perturbations.Based on the Lyapunov theory,the control law for satellite groundtrack maintenance is proposed in terms of relative mean orbital elements.Simulation results demonstrate that the proposed control scheme can effectively achieve the purpose of groundtrack maintenance.
recursive low earth orbit;groundtrack drift;groundtrack maintenance;mean orbital elements; Gauss’s variational equations
V 476.4
A
10.3969/j.issn.1001-506X.2015.03.22
温生林(1985),男,博士研究生,主要研究方向为超低轨道动力学与控制。
E-mail:wenshenglin1108@gmail.com
闫 野(1971-),男,教授,博士,主要研究方向为飞行器总体技术、飞行器动力学与控制。
E-mail:yynudt@gmail.com
张 华(1975-),男,工程师,主要研究方向为飞行器动力学与控制。E-mail:zh_bacc@126.com
网址:www.sys-ele.com
1001-506X(2015)03-0613-07
2014 05 12;
2014 09 26;网络优先出版日期:2014 11 05。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141105.1500.003.html
国防科学技术大学研究生创新基金(B140106)资助课题

