双机协同战术对策及近似最优解

赵 雨,张 斌,徐 安,李洪钶

(空军工程大学航空航天工程学院,陕西西安710038)

双机协同战术对策及近似最优解

赵 雨,张 斌,徐 安,李洪钶

(空军工程大学航空航天工程学院,陕西西安710038)

针对空战中我方双机协同对抗敌方单机的引导问题,提出了一种近似最优的接敌对策。首先,通过对几何态势的分析建立了态势模型;其次,给出了战斗机约束条件并构造了综合态势优势函数;然后,利用滚动时域控制(receding horizon control,RHC)得到了数值解;最后,给出了一个空战对抗实例。仿真结果表明,设计的接敌对策能扩大我方态势优势,占据有利发射位置,最终达到先敌发射的目标,是一种有效的战术策略。

接敌对策;协同;滚动时域控制;态势优势

0 引 言

现代空战中,协同作战已经成为基本趋势。作为协同作战的主要形式之一,火力协同是指机群成员通过对空战态势的感知和理解,采用灵活的战术改变攻击方式,从而提高整体的优势[12]。

总体上,接敌对策属于最优控制问题。对于一对一的空战对抗问题,前人已经做了大量的研究并取得了重要进展。文献[3]考虑敌我对抗因素后建立微分对策模型,并给出了数值解法的计算步骤。文献[4]讨论了信息优势的获取方法,并分析了其对空战对抗的影响。与上述文献不同的是,文献[5]综合分析了速度、距离、角度因素,以威力势为目标函数,利用改进的粒子群算法进行机动决策。相对而言,多机空战问题要复杂的多,其目标是取得整体优势的最大化[69]。针对雷达对目标探测的不确定性,合理规划我机的占位和轨迹,能有效地提高探测精度[10]。文献[11]提出了制导优势的概念,始终选择优势较大的平台发射武器。

由于策略模型是非线性的,难以得到解析解,本文根据滚动时域控制(receding horizon control,RHC)[1213]给出了近似最优的数值解法。

1 空战态势建模

1.1 问题的描述

现代空战中多为机群作战,其中双机编队是基本单元。在交战的特定阶段,由于外界环境和自身性能的限制,会出现某架战机落单的情形。本文主要研究我方双机通过战术配合接近敌方单机的策略。

空战敌我对抗中包括3个主体:我方诱饵机T、我方防御机D和敌方攻击机M。需要说明的是,诱饵机与防御机的定位不是事先确定的,而是随着态势不同时刻变化。M按照一定的引导律进行机动,减小我方的相对优势。而我方需要制定合理的策略:为了扩大我方的相对优势,T进行机动吸引M注意力,而D在保证态势优势的条件下,先于M达到武器发射条件。此外,问题的研究满足以下假设:将战斗机作为质点处理;我方双机之间信息共享,并对敌方的探测真实可靠;取地理坐标系为基准坐标系,各参数已经过相应坐标变换。

建立如图1所示坐标系。Vi、ai、i分别是战机i(i= T,M,D)的速度、法向加速度和航向角;rMD、rMT分别是M与D、T的距离;λMD、λMT分别是目标线LOSMD、LOSMT与X轴正方向的夹角。分析图1的几何关系,可以得到目标线距离变化率和角度变化率:

图1 水平面空战态势图

1.2 线性化态势模型

第1.1节的分析无法建立线性化模型,因此需要将战斗机的运动分解为沿目标线和垂直目标线两个方向。

设战斗机状态量xi=(x,y,)T分别表示位置坐标x、y和航向角,控制量u'i=(v,ω)T分别表示速度和角速度。

定义yMi为M与i(i=T,D)在垂直LOSMi上的距离。定义aMN、aTN分别为垂直LOSMT上M、T的加速度;aDN是垂直LOSMD上D的加速度,于是有

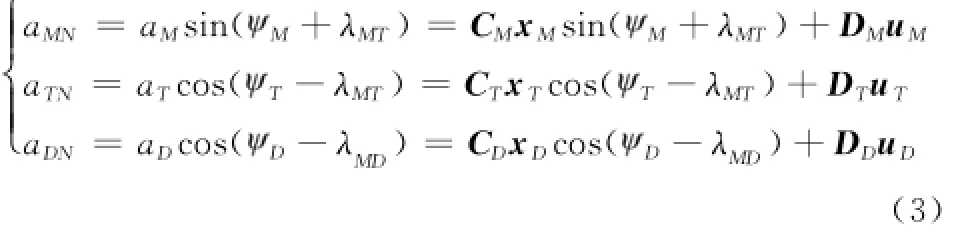
式中,Ci、Di(i=T,M,D)为时变参数,可以迭代解出;uM、uT、uD分别是垂直目标线LOSMT、LOSMD的控制量,满足:

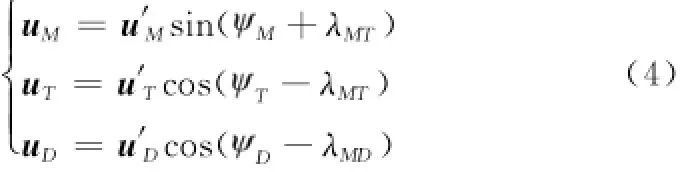
态势模型的状态量为

其维度为

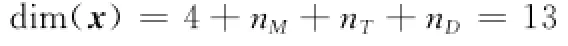
其中

态势模型可表示为

式中,Ai、Bi(i=T,M,D)为时变参数,可以迭代解出。

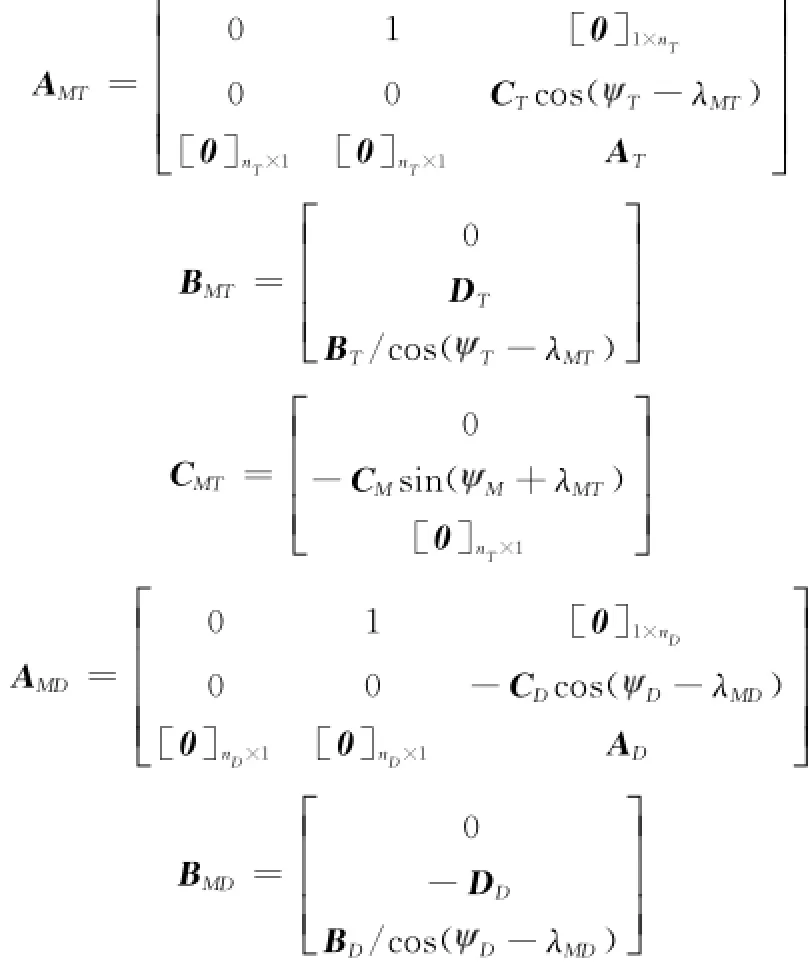
将式(1)、式(2)、式(5)代入式(6)中,整理可得

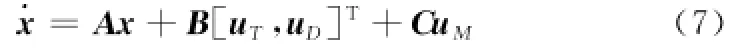
其中

并且有

2 接敌策略的约束条件及目标函数

2.1 约束条件

在真实空战中战机总是受到环境和自身性能的限制,本文主要考虑控制量约束、终端约束和引导时间约束。

控制量约束为vmin≤v≤vmax,0≤ω≤ωmax(8)

此外,接敌策略对时间有严格的要求,应保证D先于M满足武器发射条件。设D从当前时刻到发射武器时刻所需时间为tgoD;同理,M从当前时刻到发射武器时刻所需时间为tgoM。引导时间约束为

时间差Δt应满足:

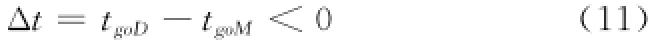
在接敌引导结束时刻tf,应满足这样的终端条件:D与M相对距离ΔrMD小于武器最大发射距离Rd,且我机前置角φ小于武器最大离轴角θmax。终端约束为

2.2 目标函数

接敌策略的目标是引导战机沿着优化的航迹机动确保空战优势,率先满足武器发射条件,从而消灭敌人,消除威胁。态势优势包括角度、距离和速度的优势。

在接敌过程中,应尽量保持我方处于敌方的尾后或侧后,此时利于武器的发射和跟踪。设我方航向角与LOS夹角为φ,敌方航向角与LOS夹角为q,并规定右偏为正,左偏为负。角度优势[14]为

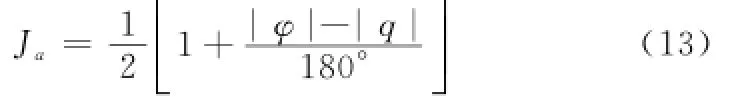
在角度优势一定的前提下,相对距离越小,则距离优势越大。设相对距离为ΔD,我方雷达探测范围为[Rrmin, Rrmax]。距离优势[11]为

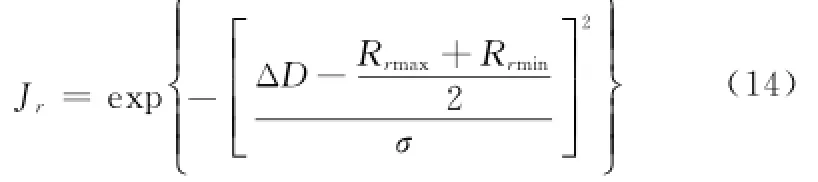
速度代表机动能力,高速度可以使战斗机占据战场主动权。设我方与敌方速度分别为Vw、Vd。速度优势[15]为

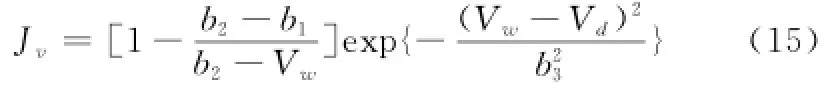
式中,b1、b2、b3是决定速度优势曲线的参数。一般情况下, b1=0.1Vd,b2=0.3Vd,b3=3Vd。

综合以上分析,态势优势可表示为

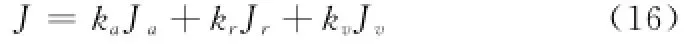
式中,ka、kr和kv分别为角度、距离和速度优势的权系数,满足ka+kr+kv=1;Ja、Jr、Jv、J的取值范围均为[0,1],且值越大,优势越明显。

敌我对抗中,态势优势是相对的。就我方而言,在对敌方形成态势优势的同时,也受到敌方的威胁。我方相对优势为

式中,ΔJiM(i=D,T)是i对于M的相对优势;JiM(i=D,T)是i对于M的态势优势;J'iM(i=D,T)是i受到M的态势威胁。

SWOT分析法[16]是对研究对象密切相关的优势(Strength)、劣势(Weakness)、机遇(Opportunity)、威胁(Threat)进行系统分析,并进行战略组合,根据不同情况制定策略的一种方法,如图2所示。

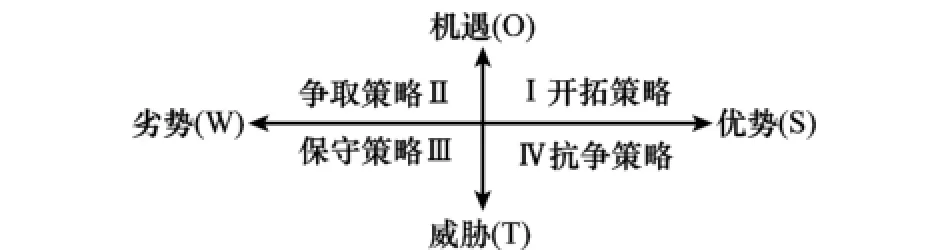
图2 SWOT选择策略

D与T应当根据各自任务采取不同策略:D采取开拓策略,尽可能地发挥性能优势,抓住进攻机会,主要考虑JDM;T采取保守策略,尽可能地隐藏性能劣势,躲避潜在的威胁,主要考虑J'TM。另一方面,T受到M的威胁,J'TM可近似为M对于T的优势JMT。

我方始终通过机动扩大相对优势,而敌方始终要缩小相对优势,即目标函数可表示为

3 近似最优的控制过程

3.1 基于RHC的控制量解算

RHC的思路是把控制过程离散化,设定预测时域Tp,将当前状态量x(tk)作为输入量,在时域t∈[tk,tk+Tp]上求解非线性规划:

式中,状态方程是式(7)的标准形式,控制量约束g(·)通过式(8)～式(11)求解,终端约束h(·)通过式(12)求解。

这样,就将一个连续的终端状态固定且控制量受约束的最优化问题转化为离散的非线性规划问题。只要输入每个初始时刻敌我双方的状态量,就可以输出每个终端时刻的双方状态量与控制量。需要说明的是,RHC只能得到预测时域Tp内的最优解。这一方面提高了运算的速度,但另一方面只是局部的最优化,所以称为近似最优接敌策略。本文将Tp作为一个常数处理。

3.2 接敌策略的控制过程

步骤1 初始化双方的状态量、控制量,设定预测时域、权系数等常数。

步骤2 根据状态方程及约束解非线性规划,输出末端时刻战机i(i=T,D,M)的状态量xi(tk+Tp)和控制量ui(tk+Tp)。

步骤3 计算相对距离、目标线角速度、遭遇时间等态势参数,解出相对优势ΔJ(tk+Tp)。

步骤4 判断是否满足终端条件。满足跳到步骤5;否则记步数加1,更新i(i=T,D,M)的状态量、控制量,跳到步骤2。

步骤5 输出状态向量、控制量向量、引导时间、优势函数等参数,结束计算。

4 仿真分析

初始条件设定:战斗机速度范围[200 m/s,1 000 m/s],角速度范围[-0.1 rad/s,0.1 rad/s]。T与D的初始坐标均为[-70 km,80 km],航向角均为-30°,M的初始坐标为[0,0],航向角为80°;Rd为35 km,θmax为±20°;态势优势权系数ka、kr和kv分别为0.4、0.3、0.3,仿真步长为0.5 s,Tp为5 s。仿真结果如图3所示,T采取类似S机动的策略,这是为了降低受到的威胁;M为了获取态势优势,被迫跟随T进行机动;而D的策略类似圆弧机动,争取尽快到达M侧方,获得较大的角度优势。总体上,我方策略类似于水平散开,T负责吸引M注意力,D抢占有利发射位置,最终率先发射武器。

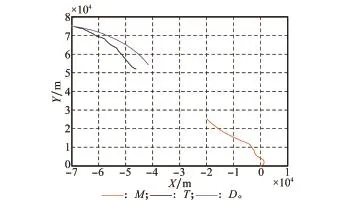
图3 水平面接敌策略

由表1可得,D首先达到武器发射条件,时间差为4.15 s。此外,D比M的前置角小4.67°,相对距离小1.41 km,说明前者发射条件更优。

表1 终端参数

在图4中,仿真时间为118 s。在t∈[1,40],T与D状态参数几乎相同,ΔJ在0附近变化。在t∈[41,118],ΔJDM逐渐增大,ΔJTM逐渐减小,这主要是因为敌我相对距离变小;另一方面,D相比M角度优势更明显,所以ΔJ逐渐变大。接敌过程中,由于敌我速度优势的变化,导致态势优势在小范围内波动。仿真结束时,ΔJDM为0.76,ΔJTM为-0.49, ΔJ为0.27,说明我方占据优势。

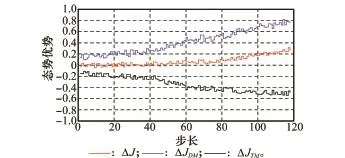
图4 态势优势变化

5 结 论

本文主要解决了双机协同下的接敌策略。建立了综合态势优势,并考虑到敌我对抗因素,从而模型更加真实可靠。此外,RHC方法简单易行,计算量小。仿真结果表明,我方通过战术机动,占据有利位置并先敌发射武器。该模型是多对多空战的简化,对研究机群协同作战的战术战法具有重要意义。四代机具有突出的隐身能力和电子干扰能力,这将制约我方对敌方运动参数的获取和机动预测。如何利用编队间信息共享解决不完全信息下的战术接敌问题是下阶段研究的重点。

[1]Yao Z X,Li M,Chen Z J.Situation analysis method for multiaircraft cooperated attack against multiple targets[J].Systems Engineering and Electronics,2008,30(2):292-296.(姚宗信,李明,陈宗基.多空中作战平台协同对抗多目标态势分析方法[J].系统工程与电子技术,2008,30(2):292-296.)

[2]Li Y,Dong Y N.Weapon-target assignment based on simulated annealing and discrete particle swarm optimization in cooperative air combat[J].Acta Aeronautica et Astronautica Sinica,2010, 31(3):626-631.(李俨,董玉娜.基于SA-DPSO混合优化算法的协同空战火力分配[J].航空学报,2010,31(3):626 631.)

[3]Kazuhiro H,Bruce A C.Optimal fighter pursuit-evasion maneuvers foundvia two-sided optimization[J].Journal of Guidance, Control,and Dynamics,2006,29(1):105-112.

[4]He J H,Gao X G.An algorithm based on game theory for exploring how to obtain NCW information superiority in 1 vs 1 air combat[J].Journal of Northwestern Polytechnical University,2008,26(2):142-145.(何建华,高晓光.基于网络中心站的一对一空战信息优势分析[J].西北工业大学学报,2008,26(2): 142-145.)

[5]Zhang T,Yu L,Zhou Z L,et al.Decision-making for air combat maneuvering based on hybrid algorithm[J].Systems Engineering and Electronics,2013,35(7):1445-1450.(张涛,于雷,周中良,等.基于混合算法的空战机动决策[J].系统工程与电子技术,2013,35(7):1445-1450.)

[6]Virtanen K,Karelahti J,Raivio T.Modeling air combat by a moving horizon influence diagram game[J].Journal of Guidance,Control,and Dynamics,2006,29(5):1080-1091.

[7]Shima T,Rasmussen S J,Sparks A G.UAV cooperative multiple task assignments using genetic algorithms[C]∥Proc.of the American Control Conference,2005:2989-2994.

[8]Liu B,Tan Z,Shao L P.Air combat decision making for coordinated multiple target attack using collective intelligence[J].Acta Aeronautica et Astronautica Sinic,2009,30(9):1727-1739. (刘波,覃征,邵利平.基于群集智能的协同多目标攻击空战决策[J].航空学报,2009,30(9):1727-1739.)

[9]Fu Z W,Yu L,Zhou Z L,et al.Research on coordinated targeting modeling and precision for double fighter[J].Journal of Air Force Engineering University(Natural Science),2013,14 (1):5-10.(付朝旺,于雷,周中良,等.双机协同攻击指令瞄准建模及精度研究[J].空军工程大学学报(自然科学版),2013,14 (1):5-10.)

[10]Gao J,Tong M A.Cooperative target detection in team air combat and optimal of search capability[J].Systems Engineering and Electronics,2004,26(3):350-353.(高坚,佟明安.编队协同对空目标探测及搜索能力的最优分配[J].系统工程与电子技术,2004,26(3):350-353.)

[11]Xiao B S,Fang Y W,Hu S G,et al.Decision methods for cooprerative guidance in multi-aircraft air warfare[J].Systems Engineering and Electronics,2009,31(3):610-612.(肖冰松,方洋旺,胡诗国,等.多机空战协同制导决策方法[J].系统工程与电子技术,2009,31(3):610-612.)

[12]Virtanen K,Karelahti J,Raivio T.Modeling air combat by a moving horizon influence diagram game[J].Journal of Guidance,Control,and Dynamics,2006,29(5):1080-1091.

[13]Wen J W,Liu F.Receding horizon control for constrained Markovian jump linear systems with bounded disturbance[J]. Journal of Dynamic Systems,Measurement,and Control,2011,13 (1):1-10.

[14]Li W X,Huang C Q,Wang Y,et al.Modeling and simulation of air combat situation assessment’s angle superiority in three dimensional space[J].Electronics Optics&Control,2012,19(2): 21-25.(李望西,黄长强,王勇,等.三维空间空战态势评估角度优势建模与仿真[J].光电与控制,2012,19(2):21-25.)

[15]Wu W H,Zhou S Y,Gao L,et al.Improvements of situation assessment for beyond-visual-range air combat based on missile launching envelope analysis[J].Systems Engineering and Electronics,2011,33(12):2679 2685.(吴文海,周思羽,高丽,等.基于导弹攻击区的超视距空战态势评估改进[J].系统工程与电子技术,2011,33(12):2679-2685.)

[16]Guo R,Yang H Z.Roadmap of renewable energy industry development in chongming ecoisland[J].Journal of Tongji University(Natural Science),2012,10(8):1204 1209.(郭茹,杨海真.崇明生态岛可再生能源产业发展路径[J].同济大学学报(自然科学版),2012,10(8):1204 1209.)

Two-fighter cooperative tactics maneuvering game and approximate optimal solution

ZHAO Yu,ZHANG Bin,XU An,LI Hong-ke
(School of Aeronautics and Astronautics,Air Force Engineering University,Xi’an 710038,China)

To solve the guidance problem of two planes cooperatively fighting with a single enemy fighter in air combat,an approximate optimum of the engagement maneuvering game is proposed.Firstly,through analyzing the geometry state,the state model the is built.Then,the plane’s restrictions are put forward and the advantage function of the integration state is constructed.Thirdly,a numerical solution using receding horizon control(RHC)is obtained.Finally,an air fight example is advanced.The results show that the designed game can maximize the state advantage,take favorable launching position and finally shoot before the enemy does.In sum,it is a quite effective engagement maneuvering strategy.

maneuvering game;cooperation;receding horizon control(RHC);state advantage

V 271.4

A

10.3969/j.issn.1001-506X.2015.03.18

赵 雨(1989-),男,博士研究生,主要研究方向为航空火力指挥与电子综合。

E-mail:zhaoyu106@163.com

张 斌(1963-),男,副教授,博士,主要研究方向为航空火力指挥与电子综合。

E-mail:zhangbin321@126.com

李洪钶(1990-),男,硕士研究生,主要研究方向为航空火力指挥与电子综合。

E-mail:Jack_Li523@google.com

徐 安(1982-),男,博士,主要研究方向为航空火力指挥与电子综合。

E-mail:Xuan82110@163.com

k=127

1001-506X(2015)03-0594-05

网址:www.sys-ele.com

文章编号:1001-506X(2015)03-0589-05

2014 04 08;

2014 06 10;网络优先出版日期:2014 08 20。

网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20140820.1733.005.html

航空科学基金(20095196012)资助课题

网址:www.sys-ele.com