综合多特征的高分辨率极化SAR图像分割
刘修国,陈 奇,陈启浩,徐 乔
(中国地质大学(武汉)信息工程学院,湖北武汉430074)
综合多特征的高分辨率极化SAR图像分割
刘修国,陈 奇,陈启浩,徐 乔
(中国地质大学(武汉)信息工程学院,湖北武汉430074)
针对高空间分辨率全极化数据的特点,基于分形网络演化分割算法框架,本文提出了一种综合K分布统计特征、Pauli分解特征和空间形状特征的高分辨率全极化SAR图像分割方法。该方法采用对数似然函数定义K分布统计特征异质度,对Pauli分解特征加权定义极化分解特征异质度。在此基础上,综合统计、极化分解和形状特征构建对象相似性准则,建立高分辨率全极化SAR图像多特征综合分割流程。通过模拟数据和ESAR全极化数据实验并与其他分割方法比较,验证了本文分割方法的有效性。
极化合成孔径雷达;分割;高分辨率;K分布;分形网络演化算法
0 引 言
分割是合成孔径雷达(synthetic aperture radar,SAR)图像分析的一个重要且持续发展的手段,准确的分割对后续地物分类和地表参数提取具有重要意义。高分辨率全极化SAR图像的空间纹理信息丰富,而且相干斑噪声使得地物边界模糊,利用单一的特征难以准确分析和提取信息。多特征综合分割是解决该问题的有效方法之一,目前相关的研究主要考虑统计特征和空间信息等的利用。
____综合利用统计特征方面,多视极化SAR协方差矩阵或相干矩阵一般采用Wishart建模,基于Wishart分布推导出的最大似然距离[1]、似然比检验距离[2]、修正的Wishart距离[3]等已广泛应用到全极化SAR图像的分割和分类中。然而,随着空间分辨率的提高,Wishart分布模型难以描述纹理丰富的非均质地表。基于乘积模型的K分布[4]由于具有很好的物理意义,能有效对非均质区建模。已有学者将其应用于全极化SAR图像的分割和分类并证明了其优势。文献[5]根据最大似然估计推导出对象间的K分布相似性准则并利用凝聚的层次聚类法对极化SAR图像进行分割;文献[6]利用K分布对协方差矩阵建模,并采用有限混合模型进行聚类。
综合利用空间信息方面,马尔可夫随机场由于可以较好地描述邻域信息,已被用于全极化SAR图像分割[7[10]。一些学者将其引入到全极化SAR图像分割,分别将形状特征与H/α/A分解特征[11]、Freeman分解特征[12]、Pauli分解特征[13]、针对建筑目标的多个极化特征[14]综合进行分割。这类方法取得了不错的分割效果,但主要是利用目标分解特征和功率进行分割,而没有考虑高分辨率全极化SAR协方差矩阵或相干矩阵特有的统计特性进行分割。
本文针对高空间分辨率全极化SAR图像空间形状和纹理信息丰富的特点,考虑到对图像的相干斑统计、极化目标分解参数和空间形状等多方面特征的充分利用,在分形网络演化分割理论的基础上,提出一种综合多特征的高分辨率全极化SAR图像分割方法。该方法基于相干矩阵的K分布假设构建统计特征相似性准则,利用相干矩阵的Pauli分解构建极化分解特征相似性准则,然后建立全极化SAR图像多特征综合分割流程,并通过模拟数据和高分辨率ESAR全极化数据验证了本文方法的有效性。
1 高分辨率全极化数据K分布
高空间分辨率全极化数据中目标的纹理细节丰富,分辨单元内的子散射子的数目较少,不再满足高斯模型假设,特别是在非均质的城区和林地,更适宜采用非高斯的乘积模型进行建模。
1.1 多视极化数据K分布模型
在满足互易定理的情况下,单站全极化SAR的散射矩阵经Pauli基矢量化后可得:

式中,T表示转置。为了减少相干斑的影响,需要进行多视处理。多视相干矩阵定义为

式中,〈·〉表示取平均;l为视数;H表示共轭转置。
乘积模型将散射矢量表示为一个随机变量的平方根和一个散射矢量的乘积:

式中,g是均值为1的标量,用来描述地表纹理,反映了真实的雷达后向散射功率的空间变化;k'为完全发育的相干斑分量,服从多维复高斯分布。
由于纹理比相干斑在更广范围内具有更高的空间相关性,因此在视数较小时可以假设纹理变量与i无关,将式(3)代入式(2)中得:式中,多视矩阵T'服从复Wishart分布。

当g服从伽马分布时,则多视相干矩阵T服从K分布[15]:
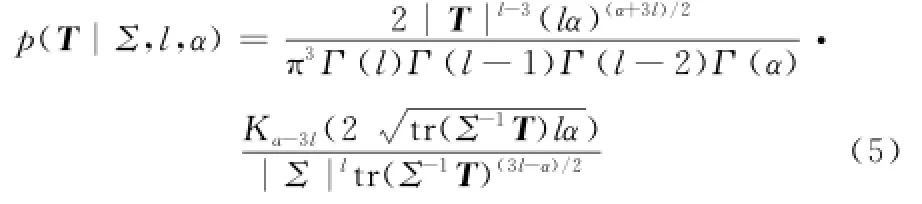
式中,Σ=E[kkH],表示相干矩阵的数学期望;Γ(·)为Γ-函数;tr(·)和|·|分别表示矩阵的迹和行列式;Kv(·)为第二类修正的贝塞尔函数;α为形状参数。当l=1时即为单视极化数据K分布;当α→∞时,T趋于Wishart分布。
K分布能有效对均质区和非均质区建模,已逐步应用于极化SAR图像的分割和分类中。
1.2 K分布模型参数估计
模型中参数的估计直接关系到分布模型拟合的效果。Σ为相干矩阵的期望值,其估计值^Σ可以由样本的平均值来估算:

由于实际数据之间存在着空间相关性,式(5)中的视数l应由等效视数代替,即参与多视平均时等效的独立样本个数,一般比名义上进行多视平均的视数要小。对于极化SAR数据的等效视数l和形状参数α的估算方法目前有两类,一类是对3个极化通道分别估算后取平均值;另一类是直接利用相干矩阵或协方差矩阵进行估算[16]。后者利用了更多的极化信息,估算的效果更好。
本文极化SAR数据的等效视数的估算采用文献[16]提出的矩阵对数累积量方法来估算,单站情况下,其估算式为

极化数据K分布的形状参数α的估算也可以采用文献[16]提出的矩阵对数累积量来估算,但该方法较复杂,计算量巨大;由于在后续的分割过程中需要反复的估算合并对象的形状参数,因此本文选择文献[17]提出的估算方法。该方法也是直接利用相干矩阵或协方差矩阵进行估算且计算更为简单。单站情况下,估计值^α的估计式如下:
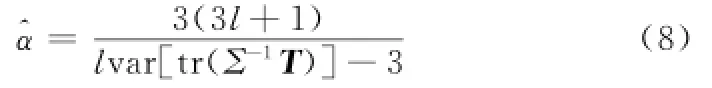
式中,var(·)表示求样本的方差。
2 综合多特征的全极化图像分割
FNEA分割的基本思想为:利用分形迭代过程,按照相似性最大的合并准则,从像素开始合并满足条件的两相邻对象。对象是由特征相似、空间聚集的像素所构成的像素集合。理想的分割结果要求对象被合并到与之最相似的邻近对象中,这满足对象异质度均值最小的分割结果评价标准。
因此,合并前后异质度的变化是对象相似性描述的一个重要指标。设对象的异质度为h,对象内像素个数为n,则两个相邻对象的相似性可由异质度的变化Δh描述:

式中,下标1,2和m分别代表合并前相邻的对象1、对象2和合并后的新对象m,下同。显然Δh越小,则相邻两对象的相似性越高。
现有的分形网络演化分割通过特征标准差和形状参数构建异质度量测准则,没有考虑极化SAR协方差或相干矩阵特有的统计特征,解决综合统计、极化分解和空间形状等多特征分割的关键在于如何构建新的综合多特征的对象相似度测量准则。
2.1 综合相似性准则
FNEA分割过程中关键步骤是对象间相似性的计算。高分辨率全极化SAR数据具有丰富的纹理信息、极化物理散射特征和空间特征,对象间的相似性包括统计特性、极化分解特征和空间形状特征等多方面。
2.1.1 统计相似性准则
FNEA分割过程中对象光谱特征异质度是通过将对象中各个特征波段的标准差加权求和来得到的,该方法并没有考虑数据的统计分布模型,且忽略了各个波段数据的相关性,因而不能完全利用极化SAR协方差矩阵或相干矩阵信息。为了有效的利用矩阵各方面的信息,有必要以矩阵为基本的处理单元,并考虑目标的统计分布模型来定义对象间的统计相似性准则。
本文采用文献[5]提出的最大对数似然函数来计算对象的统计相似性。对象S的统计特性异质度hstt可以用该对象中像素的最大对数似然函数来计算
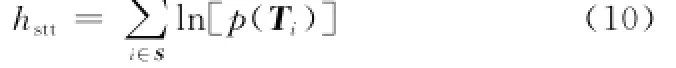
FNEA分割过程中,每次融合两个相邻对象产生新的对象都会使对数似然函数值下降。将合并前后对数似然函数值下降最少的相邻两对象进行合并。因此,不同于式(9),统计相似性准则可以表示为

式中,统计异质度h为对象的最大对数似然函数,该值的计算需要事先给定对象的概率密度函数,并且其参数由对象中像素按照式(6)~式(8)进行估算。
由式(5)和式(10),可得对象S的K分布统计特征异质度:

式中,ns为对象S内的像素数目。将式(12)代入式(11)中,可求得相邻两对象间统计相似性准则Δhstt。
2.1.2 极化分解特征相似性描述
目标分解参数是描述极化SAR图像地物目标的一类重要特征。考虑到Pauli分解RGB合成图作为极化SAR图像的标准显示方式,且分解后的3个分量功率对应于相干矩阵对角线上的元素,不需要额外的分解算法,同时Pauli分解3个分量分别代表奇次散射、偶次散射和倾斜45°的二面角散射,也具有明显的物理意义。因此本文利用Pauli分解后的特征计算极化分解特征异质度。由于不同传感器极化数据的极化分解功率特征存在一定差异,统一将Pauli分解的三分量拉伸到[0,255]范围。
采用经典的各功率特征标准差加权来计算极化分解功率异质度,各功率权重相等,代入式(9)中,则极化SAR图像对象间极化分解特征的相似性准则Δhdec为

式中,σ1c,σ2c,σmc分别为第c个极化分解功率特征上合并前两对象及合并后对象内像素特征值的标准差。
2.1.3 形状相似性准则
形状相似性采用两对象合并前后形状特征空间内异质度的变化来描述,从紧致度和光滑度两种景观生态测度来定义。紧致度hcmpct表征对象的紧凑程度,可描述为对象边界周长p与对象内像素数n的均方根之间的比率;光滑度hsmooth表征对象边界的光滑程度,用对象边界周长p与最小外包矩形周长b间的比率来描述。设紧致度的权重为wcmpct,wcmpct∈[0,1]。由式(9)可建立对象间形状相似性准则Δhshape:

2.1.4 综合的相似性准则
在统计、极化分解和形状特征组成的多维特征空间内,两相邻对象的综合相似性可以由3种相似性的加权和来计算。由于统计和极化分解特征相似性都是描述目标对象内在的相似性,形状相似性是描述对象外在形状特性。因此,先对统计和极化分解特征相似性加权后再与形状相似性加权。
根据式(11)~式(14),设形状相似性的权重为wshape, wshape∈[0,1],极化分解特征相似性的权重为wdec,wdec∈[0,1],则任意相邻两对象间的综合相似性准则Δhtol为

显然,Δhtol越小表明对象间的相似性越大。
2.2 多特征综合FNEA分割流程
由式(15),根据相似性最大的合并准则从初始分割对象开始迭代合并满足条件的相邻对象,直到没有对象合并为止即可实现综合统计分布、空间形状和极化分解特征的极化SAR图像分割。每次迭代合并过程中都遍历每个对象,计算相邻两对象间的综合相似性Δhtol,并通过阈值ρ比较判断是否合并生成新的对象。阈值ρ是尺度s的函数,可以控制分割结果对象的大小和总数目。分割流程如图1所示,主要步骤如下:
步骤1 设置分割参数,包括尺度s、形状和统计特征和极化分解特征权重;
步骤2 预分割生成初始对象;
步骤3 遍历所有对象,对每个对象,按式(15)计算其与周围相邻对象间的相似性,取其最小值Δhmintol并判断是否达到阈值ρ,若小于ρ则合并两个对象生成新的对象;
步骤4 迭代步骤3直到相邻两次迭代没有对象合并为止;
步骤5 生成对象多边形,分割完成。
分割过程中对多特征的综合利用,面临以下几个问题:①统计相似性的计算需要足够的样本(即对象内的像素)进行参数估计,因而需考虑合适的初始分割;②如何平衡考虑各类特征权重。
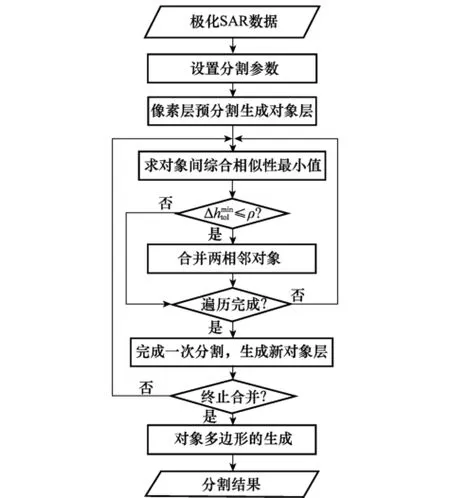
图1 综合K分布、形状和极化分解特征的分割流程
2.2.1 初始分割
统计特征的利用需要先确定K分布模型参数估计的最小样本数目,样本数过少会导致参数估计不稳定,影响统计异质度的计算。为此,采用网格划分进行初始分割,将图像划分为n×n的方格,每个方格作为一个初始对象。为了确定合适的样本数以准确估计初始对象的K分布参数,采用大小为320×320像素的模拟K分布全极化数据,计算不同网格大小情况下对象中像素数与归一化K分布相似性准则Δhstt/n的关系,见图2。可以看出,随着样本数的增加归一化相似性逐渐减少,当对象的样本数较少时波动较大。较合理的样本数在16~64之间,考虑到网格过大会导致地物边界锯齿状更明显,初始分割时采用4×4的网格划分。2.2.2 权重与尺度设置
由式(15)可知,K分布统计特征相似性、Pauli分解特征相似性和形状特征相似性的权重设置会直接影响到对象间相似度的计算,同样也会影响最终的分割结果。

图2 归一化平均统计相似性与对象像素个数的关系
为了找到特征权重调整的参考依据,使用德国Bayern南部Oberpfaffenhofen地区L波段机载ESAR全极化SAR数据,对分割过程中的每一层迭代合并结果对象,分别计算该层对象的统计、Pauli分解和形状特征的平均异质度,如图3所示。

图3 分割过程中每层对象的各特征平均异质度
图3中Pauli分解特征异质度约为K分布统计异质度的10多倍,为了保证分割过程中较平衡地考虑Pauli分解功率和统计分布特征,可以据此将Pauli分解特征权重设为0.1左右。为了突出对象内在的异质性,一般形状特征权重设置为0.2左右,其中紧致度约为0.3。
分割的尺度s也会一定程度影响分割结果,一般较小的尺度会导致分割结果琐碎,而较大的尺度会导致欠分割。由式(15)可知,综合相似性由参与分割的各类特征的相似性所决定,对于不同分割特征的权重组合,综合相似性的大小会有所不同,因此合适的分割尺度s并不是一个确定值,而应根据实际分割情况选择。
3 实验与分析
3.1 模拟全极化数据分割
实验模拟极化数据大小为320像素×320像素,包含满足K分布的4类样本数据,样本的形状参数α和相干矩阵T从德国Oberpfaffenhofen地区L波段ESAR全极化数据中选择道路、农田、植被和城区样本估算得到。模拟极化SAR数据Pauli RGB合成图如图4所示。图4中右图的红绿蓝黑色区分别代表城区、植被、农田和道路。

图4 模拟数据Puali RGB图及目标分布示意图
考虑到模拟数据较规整,为了突出不同统计和极化分解特征的特点以便比较,均不利用形状特征,开展如下实验:图5(a)利用Freeman分解三分量分割,文献[12]采用了该组特征;图5(b)利用Cloud分解的熵H、极化角α、各向异性A以及总功率Span分割,文献[11]即采用该组特征;图5(c)利用Pauli分解三分量分割,文献[13]采用了该组特征;图5(d)利用Wishart统计特征分割;图5(e)利用K统计特征分割;图5(f)本文提出的综合K统计和Pauli分解特征的分割,其中极化分解特征权重为0.1。初始分割均采用4×4网格划分,分割结果如图5所示。

图5 模拟极化数据分割结果
由图5可以看出:①利用极化分解特征的方法(a)、(b)和(c)中,(c)的分割结果最好。方法(a)对均质的道路和农田边界划分较好,但对植被中非均质的城区分割效果不理想;方法(b)对道路与植被、农田的边界划分不准确,对城区的分割比方法(a)相对要好;方法(c)对各地物的边界划分都较准确,但在被植被包围的城区因受噪声影响分割结果存在小的偏差。②利用统计特征的方法(d)和(e)中,(e)的分割结果较好。方法(d)对均质区分割效果较好,但对非均质的植被和城区边界划分不理想;方法(e)对各地物的边界划分均很准确,只是对均质的道路和农田出现过分割现象,原因是均质区的K分布形状参数估算值波动较大。③本文提出的方法(f)分割效果最好,在均质区避免了K分布特征的过分割现象且对非均质的城区和植被分割也很准确。
3.2 ESAR高分辨率全极化数据分割
为了进一步验证本文方法对真实数据的有效性,实验采用德国Oberpfaffenhofen地区L波段机载ESAR全极化SAR数据,距离向1视、方位向2视处理后,分辨率为2 m× 2 m,图像大小800像素×800像素。实验区主要包含农田、林地、城区建筑物、机场跑道和草坪等,实验区Pauli RGB合成图及参考光学图像如图6所示。

图6 ESAR全极化数据Pauli RGB图及参考光学图像
在第3.1节基础上增加利用空间形状特征,分别采用以下不同方法进行多尺度分割实验:①采用Wishart分布统计和形状特征的分割;②采用K分布统计和形状特征的分割;③增加极化分解特征,采用Wishart分布统计、形状和Pauli特征的分割;④采用K分布统计、形状和Pauli特征的分割。其中,形状参数为0.2,紧致度为0.3,Pauli特征权重为0.1。参照同时期的光学图像选取地表覆盖样本,采用重叠度方法[18]统计分割结果精度,同时综合考虑结果对象数目,在确保分割精度情况下对象数目越少越好。采用不同特征、分割尺度的结果精度评价见表1。

表1 分割特征、尺度及结果精度评价
为了直观地比较采用不同统计特征的分割效果,从结果精度和对象数目两方面进行比较,图7给出了不同方法的分割精度与对象数目的关系。

图7 分割精度与对象数目的关系
由表1和图7可见,随着尺度增大,分割结果对象数目逐渐减少,同时分割精度也逐渐降低。原因是对象越少在地类边界处越容易产生欠分割,从而降低精度。比较方法①和方法②的分割结果,在相近的结果对象数目的情况下,利用K分布分割的尺度要比Wishart分布分割的尺度小,说明K分布的平均相似性要小于Wishart分布的平均相似性;另外,方法①尺度为20时,分割精度超过85%且对象数控制在400左右;方法②尺度为15时较合适,分割精度超过86%且对象数相对更少。增加Pauli分解特征后,在相同结果对象数目情况下,综合3种特征后的分割结果精度更高。在相同的结果对象数目的情况下,利用K分布分割的结果精度要好于利用Wishart分布分割的结果;达到相同的分割精度,利用K分布统计特征分割的结果对象数更少。综合结果精度和对象数目考虑,方法④分割效果最好。
方法①尺度为20和方法②尺度为15的分割结果如图8所示。可以看出,方法②对非均质的林地和城区分割的结果对象数比方法①更少,边界划分也更合理。另一方面,在几处均质农田区,方法②分割相对零碎,与模拟数据实验方法(e)吻合。
增加Pauli分解特征后,在尺度参数为30时,方法③和方法④的分割结果如图9所示。同样可以看出,利用K分布的分割在非均质的林地和城区结果对象数要比利用Wishart分布分割的更少,边界划分也更合理。比较图8和图9发现,增加Pauli分解特征后,方法④对林地的边缘及内部的划分更准确,对城区建筑物的内部细节划分更精细,表明增加的Pauli分解特征提升了对局部细节特征的描述。同时,对均质的农田和机场跑道划分更加完整,表明增加Pauli分解特征后能有效避免只利用K分布统计特征的过分割现象。
最后,与eCognition软件中分割方法进行对比。在对相干矩阵分割前,进行4×4的棋盘预分割以抑制噪声。分割的尺度参数为55,形状参数为0.2,紧致度为0.3,结果如图10所示。可以看出,在林地和城区中存在明显的过分割现象。主要原因在于高分辨率全极化SAR图像中非均质的林地和城区满足K分布,而eCognition软件中分割算法主要针对满足高斯分布的高分辨率光学图像来设计的,其对象的光谱相似性是通过标准差的变化来计算。由于在林地、城区等区域地表存在明显的纹理变化,标准差变化比均质的农田、道路等大很多,因而出现严重的过分割现象。而本文方法采用更适合的K分布统计模型,能更好地利用高分辨率极化SAR图像中地物目标相干矩阵的统计特性,分割效果更好。
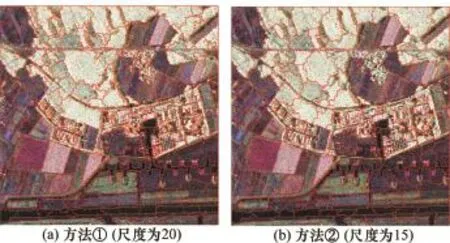
图8 综合统计和形状分割结果

图9 综合统计、形状和Pauli分解特征分割结果

图10 eCognition软件分割结果
4 结 论
本文提出的一种综合多特征的高分辨率全极化SAR图像分形网络演化分割方法,通过定义K分布统计特征、Pauli分解特征的相似性准则,能综合高分辨率极化SAR图像的统计、极化分解和空间形状3类特征进行分割。实验结果证明了本文提出的充分利用3方面特征分割方法的有效性,在高分辨率极化SAR图像中的林地和城区等异质区K准则比Wishart准则划分更合理,Pauli分解特征在均质的农田区分割以及图像局部细节上更有优势。对于均质区的分割,Wishart分布特征较K分布特征要好,因此,利用将两者结合的自适应统计特征的分割将是后续工作的一个重点。
[1]Lee JS,Grunes M R,Kwok R.Classification of multi-look polarimetric SAR imagery based on complex Wishart distribution[J].International Journal of Remote Sensing,1994,15(11):2299-2311.
[2]Conradsen K,Nielsen A A,Schou J,et al.A test statistic in the complex wishart distribution and its application to change detection in polarimetric SAR data[J].IEEE Trans.on Geoscience and Remote Sensing,2003,41(1):4 19.
[3]Kersten P R,Lee JS,Ainsworth T L.Unsupervised classification of polarimetric synthetic aperture radar images using fuzzy clustering and EM clustering[J].IEEE Trans.on Geoscience and Remote Sensing,2005,43(3):519-527.
[4]Lee JS,Schuler D L,Lang R H,et al.K-distribution for multilook processed polarimetric SAR imagery[C]∥Proc.of the Geoscience and Remote Sensing Symposium,1994:2179 2181.
[5]Beaulieu J M,Touzi R.Segmentation of textured polarimetric SAR scenes by likelihood approximation[J].IEEE Trans.on Geoscience and Remote Sensing,2004,42(10):2063-2072.
[6]Doulgeris A P,Anfinsen S N,Eltoft T.Classification with a non-Gaussian model for POLSAR data[J].IEEE Trans.on Geoscience and Remote Sensing,2008,46(10):2999-3009.
[7]Wu Y H,Ji K F,Li Y,et al.Segmentation of multi-look fully polarimetric SAR images based on wishart distribution and MRF[J]. Acta Electronica Sinica,2007,35(12):2302-2306.(吴永辉,计科峰,李禹,等.基于Wishart分布和MRF的多视全极化SAR图像分割[J].电子学报,2007,35(12):2302-2306.)
[8]Zhang T,Hu F M,Yang R L.Detail-preserving segmentation of polarimetric synthetic aperture radar data[J].Systems Engineering and Electronics,2009,31(10):2372-2375.(张涛,胡风明,杨汝良.极化SAR数据的细节保持分割[J].系统工程与电子技术, 2009,31(10):2372-2375.)
[9]Akbari V,Doulgeris A P,Moser G,et al.A textural-contextual model for unsupervised segmentation of multipolarization synthetic aperture radar images[J].IEEE Trans.on Geoscience and Remote Sensing,2013,51(4):2442-2453.
[10]Hay G J,Blaschke T,Marceau D J,et al.A comparison of three image-object methods for the multiscale analysis of landscape structure[J].ISPRS Journal of Photogrammetry and Remote Sensing,2003,57(5/6):327-345.
[11]Benz U,Pottier E.Object based analysis of polarimetric SAR data in alpha-entropy-anisotropy decomposition using fuzzy classification by ecognition[C]∥Proc.of the Geoscience and Remote Sensing Symposium,2001:1427-1429.
[12]Gao H,Yang K,Jia Y.Segmentation of polarimetric SAR image using object-oriented strategy[C]∥Proc.of the Remote Sensing,2nd International Conference on Environment and Transportation Engineering,2012:1-5.
[13]Qi Z X,Anthony G Y,Li X,et al.A novel algorithm for land use and land cover classification using radarsat-2 polarimetric SAR data[J].Remote Sensing of Environment.2012,118 (2012):21-39.
[14]Huang X D,Liu X G,Chen Q H,et al.An integrated multicharacteristics buildings segmentation model of POLSAR images[J].Geomatics and Information Science of Wuhan University,2013,38(4):450-454.(黄晓东,刘修国,陈启浩,等.一种综合多特征的全极化SAR建筑物分割模型[J].武汉大学学报(信息科学版),2013,38(4):450-454.)
[15]Lee J S,Pottier E.Polarimetric radar imaging from basics to application[M].U.S.:Taylor&Francis Group,2009.
[16]Anfinsen S N,Eltoft T.Application of the matrix-variate mellin transform to analysis of polarimetric radar images[J].IEEE Trans.on Geoscience and Remote Sensing,2011,49(6):2281-2295.
[17]Doulgeris A P,Anfinsen S N,Eltoft T.Classification with a non-gaussian model for POLSAR data[J].IEEE Trans.on Geoscience and Remote Sensing,2008,46(10):2999-3009.
[18]Möller M,Lymburner L,Volk M.The comparison index:a tool for assessing the accuracy of image segmentation[J].International Journal of Applied Earth Observation and Geoinformation,2007,9(3):311- 321.
陈启浩(1982-),通信作者,男,讲师,博士,主要研究方向为极化SAR图像处理与信息提取。
E-mail:cugcqh@163.com
徐 乔(1991-),男,硕士研究生,主要研究方向为极化SAR信息提取。
E-mail:xu_qiao_cug@126.com
Integrated multi-feature segmentation method for high resolution polarimetric SAR images
LIU Xiu-guo,CHEN Qi,CHEN Qi-hao,XU Qiao
(School of Information Engineering,China University of Geosciences,Wuhan 430074,China)
This paper proposed a novel segmentation method which integrates statistical distribution,geometric shape features and polarimetric decomposition features for high resolution polarimetric synthetic aperture radar(SAR)data.This method is based on the fractal network evolution algorithm(FNEA)that integrates K distribution statistics and Pauli decomposition features.Specifically,statistical heterogeneity of objects is defined by the maximum log likelihood function based on K distribution.Polarimetric decomposition heterogeneity of objects is calculated through the weighted sum of standard deviation of Pauli decomposition features.A total heterogeneity of objects is defined by the weighted sum of statistical heterogeneity,polarimetric decomposition heterogeneity and shape heterogeneity.Then,the multi-feature segmentation procedure for high resolution polarimetric SAR data is constructed.The effectiveness of the integrated multi-feature segmentation we develope is demonstrated by simulated data and L band E-SAR polarimetric data.
polarimetric synthetic aperture radar(SAR);segmentation;high resolution;K distribution; fractal network evolution algorithm
TN 957.52
A
10.3969/j.issn.1001-506X.2015.03.12
刘修国(1969-),男,教授,博士,主要研究方向为遥感图像信息提取与3S集成方向的研究。
E-mail:liuxg318@163.com
陈 奇(1989-),男,硕士研究生,主要研究方向为极化SAR信息提取。
E-mail:chenqi106@foxmail.com
网址:www.sys-ele.com
1001-506X(2015)03-0553-07
2014- 04-01;
2014- 07-08;网络优先出版日期:2014- 10-17。
网络优先出版地址:http:∥w ww.cnki.net/kcms/detail/11.2422.TN.20141017.1611.012.html
国家自然科学基金(41301477,41471355);中国博士后科学基金(2012M521497);武汉市学科带头人计划项目(201271130443)资助课题

