矿山开采沉陷参数灵敏度及关联度分析∗

刘 浪，马岳谭，何远富

(1.西安科技大学能源学院, 陕西西安 710054；2.西部矿井开采及灾害防治教育部重点实验室,陕西西安 710054；3.长沙矿山研究院有限责任公司, 湖南长沙 410012)

矿山开采沉陷参数灵敏度及关联度分析∗

刘 浪1，2，马岳谭1，2，何远富3

(1.西安科技大学能源学院, 陕西西安 710054；2.西部矿井开采及灾害防治教育部重点实验室,陕西西安 710054；3.长沙矿山研究院有限责任公司, 湖南长沙 410012)

以某矿典型的地表移动观测站数据作为训练样本和测试样本，建立了矿山开采沉陷的神经网络与灰色关联模型。利用神经网络输出变量对输入变量的偏导数求解下沉系数的影响因素的灵敏度，推导了利用神经网络计算灵敏度的公式，同时利用灰色综合关联分析法计算开采下沉系数与各影响因素的关联度。结果表明，松散层厚度的神经网络灵敏度和灰色关联度皆最大，深厚比次之，而倾角最小，该结论为矿山开采沉陷的分析与控制提供了一定的理论基础。

矿山沉陷；下沉系数；神经网络；灵敏度分析

随着浅部资源逐渐减少和枯竭,开采深度越来越大,目前我国面临深部开采的矿山占全国矿山总数的90%[1-6]。在深部矿产资源开采过程中,采场围岩的岩石力学性质、地应力等地质特性与浅部比较均发生了根本的变化,岩层发生变形、位移和崩落等现象频繁发生,进而引起地表沉陷等,导致地质灾害及地表构筑物破坏等。矿山开采沉陷系数对于描述由于采矿引起的地表移动规律至关重要,然而影响矿山开采沉陷系数的因素很多,并且各因素之间存在非线性关系[7-13]。人工神经网络具有强大的动态非线性信息处理能力,可用来计算或预测地表下沉系数,在开采沉陷工程等领域得到成功应用[14-15],同时灰色关联分析法的引入使得关于开采沉陷系数与影响因素的相关性研究更加科学可靠。但是,如何确定每个影响因素的重要程度即灵敏关联度,成为关注的焦点。掌握了影响因素的灵敏关联度,可为掌握开采沉陷规律,控制开采沉陷提供依据。

影响因素的灵敏度即由于因素发生微小变化时输出变量发生变化的程度,用数学语言表达就是计算系统输出对系统模型输入参数的偏导数。由于矿山开采系统非常复杂,关于沉陷系数的灵敏度计算无法直接通过计算获得[16-18],用单因素分析方法也很难得到准确解[19]。而利用神经网络构建出准确的地表下沉系数模型后,再通过神经网络求出各参数的灵敏度。通过灰色综合关联分析计算得到的灰色关联度,则代表了各因素之间的关联影响程度。本文建立基于人工神经网络(Artificial Neural Network,ANN)的开采沉陷系数模型,并进行沉陷系数的参数灵敏度分析,用以确定影响下沉系数的各个参数的灵敏度指标,并运用灰色关联分析法计算各因素间的关联度,使整体结果更加科学完整。

1 基于灰色-神经网络的灵敏度与关联度模型

1.1 BP神经网络模型

单隐含层的多层BP神经网络可以任意逼近任何连续函数和它的相应的偏导数[20-21],应用最为广泛。该BP神经网络模型是由输入层、输出层和隐含层构成,每一层均有若干个神经元组成。BP神经网络的学习过程可以描述为:工作信号正向传播,输入信号从输入层经隐单元,传向输出层,在输出端产生输出信号；误差信号反向传播,网络的实际输出与期望输出之间的差值即为误差信号,误差信号由输出端开始逐层向前传播。在误差信号方向传播过程中,网络的权值由误差反馈进行调节,通过权值的不断修正使网络的实际输出更接近期望输出。

输入层向量为X＝(x1,x2,…,xn),即有n个输入信号,其中任一输入信号用x表示；隐含层向量为H＝(h1,h2,…,hl),即有l个神经元,其中任一神经元用h表示；输出层高向量用Y表示。输入层与隐含层的突触权值用wij表示,隐含层与输出层的突触权值vj表示。可用以下公式进行表示:

式中,hj是第j个隐含层单元的输出；η是输出层单元的阈值。

神经元的输入用向量xk表示,点乘突触权值wk,激励输出函数用f表示,可得:

通常情况下,使用该激励函数时β值取1。

1.1.1 网络输出对输入的偏导数

首先进行神经网络训练,当误差达到预定值后,结束训练。此时,网络结构固定,且各权值响应确定,利用链式微分法则计算神经网络的输出变量对于输入变量的偏导数。由公式(1)和公式(2),可得:

1.1.2 偏导数计算中变量的转换

对输入与输出变量的数据进行无量纲化,使得输入与输出数据在0～1之间,从而有效地缩短网络收敛时间,极大地了提高网络计算效能和计算精度。同时,采用极差规格化,既能保证原有指标的分辨力,还能对输入和输出数据实现无量纲化:

设定一组输入数据X＝[x1,x2,…,xn],则

式中,xi(i＝1,2,…,n)是原始输入变量或样本输出变量；n是样本数目；xi′是级差规格化后的xi；xmax是xi的最大值；xmin是xi的最小值。

假设有如下的映射关系:z＝g(x1,x2,…,xn),将自变量和因变量做级差规格化处理,其中,x1′,x2′,…xn′是输入神经网络的级差规格化后的变量,z'是神经网络的输出值。由神经网络求得的偏导数为:

同理可得网络输出对任意某一输入变量的偏导数值。

1.2 灰色综合关联分析

灰色关联分析方法是根据因素之间的发展态势的相似或相异的程度来衡量因素之间的关联程度。关联度用以反映评价对象对于理想对象的接近次序,即评价对象的优劣次序,其中灰色关联度最大的评价对象为最优。利用灰色绝对、相对和综合关联度对开采沉陷系数影响因素进行分析,根据各因素数据曲线的相近程度,用以表征各因素间的关联度。

1.2.1 灰色绝对关联度

设定影响开采沉陷系数的影响因素为Xi,对原始数据进行预处理,其具体计算步骤如下:

步骤一:应用始点的零化算子对Xi＝(xi(1),xi(2),…,xi(n))与X0＝(x0(1),x0(2),…,x0(n))进行始点零化像处理,即:

经过始点零化像处理后的Xi与X0,记为Xi0与X0 0。

步骤三:得出数列Xi和X0的灰色绝对关联度,即:

1.2.2 灰色相对关联度

1.2.3 灰色综合关联度

灰色综合关联度能较为全面表征序列之间关系是否紧密的一个数量指标(一般计算时可取θ＝0.5),可以同时反映出两组数据序列Xi与X0折线的相似程度和两折线相对于始点的变化速率的接近程度,数据序列Xi与X0的灰色综合关联度计算公式如下:

2 开采沉陷参数因素的灵敏度及关联度分析

2.1 下沉系数的神经网络模型

地表开采沉陷的主要影响因素来自矿床地质构造及采矿,由于现有的开采沉陷实例缺乏足够的资料积累,并为了构建足够精确的模型便于灵敏度分析的考虑,本文使用的典型工作面观测站地表移动实测参数的数据中,开采方法均系采用走向长壁式采煤、全部垮落法管理顶板,影响开采沉陷系数的主要因素有煤层倾角、深厚比、松散层厚度等。因此,将倾角、深厚比和松散层厚度作为输入参数,将地表开采沉陷系数作为输出参数。

文献[22]中200个地表移动观测站的测量数据,从中选出30组数据作为训练样本和测试样本,如表1所示。将1～25组数据作为训练样本,将26～30组数据作为测试样本。

神经网络输入层3个单元,输出层1个单元,利用试凑法确定隐含层神经元数目为8个,采用3-8-1的结构。训练时,设定目标误差为0.005。将表1中的26-30组数据测试样本,用以检验训练好的网络优劣性,开采沉陷系数预测结果与实测值的比较如表2所示。由表2可知,开采沉陷系数的相对误差基本控制在10%以内,说明所构建的网络模型有较高的精度,为后面分析开采沉陷影响因素的灵敏度提供保证。

表1 训练与检测样本

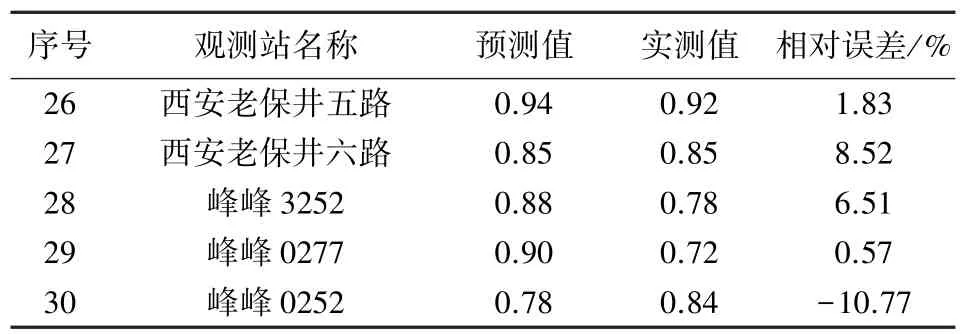
表2 下沉系数预测结果与实测值的比较

2.2 灵敏度计算结果与分析

利用式(11),计算30组样本点处的灵敏度(见图1)。倾角的灵敏度保持正值,地表下沉系数随着倾角的增大而增大；另一方面,深厚比与松散层的灵敏度保持为负值,说明随着深厚比或者松散层厚度的增加,地表下沉系数将减小,这与实际情况相符。图2是开采沉陷影响因素在各样本点处的灵敏度绝对值的柱状图,在相同样本点处,灵敏度的绝对值最大的是松散层厚度,深厚比次之,而倾角最小。通过影响因素的平均灵敏度值比较(见图3),也可得出相同结论。

图1 各样本点处的灵敏度值

图2 样本点处灵敏度值柱状图

图3 3个因素平均灵敏度值比较

图4～图6是1个影响因素变化而另外2个因素取定值时下沉系数随该参数变化而变化的情况,从而反映了该参数对下沉系数的影响。量取定值时,深厚比为70,倾角为25°,而松散层厚度为40m。结果表明:下沉系数对于深厚比和松散层的变化较为敏感,而对于倾角的变化不敏感。

2.3 灰色关联分析计算结果与分析

依据表1数据,得出开采沉陷系数X0与各影响因素的灰色关联度(包括:绝对关联度ε、相对关联度r和综合关联度ρ),具体见表3和表4。

图4 倾角25°、松散层厚度40m时下沉系数与深厚比的关系

图5 深厚比70、松散层厚度40m时下沉系数与倾角的关系

图6 深厚比70、倾角25°时下沉系数与松散层厚度的关系

表3 灰色绝对和相对关联分析

计算得知,灰色绝对关联度比较是:ε03＜ε02＜ε01,灰色相对关联度比较是:r02＜r03＜r01,灰色综合关联度在θ取绝大部分值下都是:ρ02＜ρ03＜ρ01。由灰色绝对、相对及综合关联度表分析可得知,松散层厚度对下沉系数的影响占最大,其数据序列生成的折线与下沉系数数据序列生成的折线是最接近的,相对于始点的变化速率也是最接近的,其次是深厚比,而倾角对下沉系数的影响最弱。

表4 灰色综合关联分析表

灰色关联度的结果与神经网络灵敏度计算结果完全一致,可知松散层厚度对下沉系数影响最敏感,关联程度最大,影响程度也最大,其次是深厚比的变化,最弱是倾角的变化。

3 结 论

(1)建立了用于开采沉陷系数的BP神经网络灰色关联分析模型,开采沉陷系数的相对误差均控制在10%以内,所建网络模型有较高的精度,为工程应用提供保证。

(2)由灰色绝对、相对及综合关联度分析可知,松散层厚度对下沉系数的影响占最大,其次是深厚比,而倾角对下沉系数的影响最弱。而深厚比和松散层都比倾角大很多,故主要影响因素为松散层厚度和深厚比。从而在实际工程中,对于这2个因素引起的效应要予以足够的重视。

(3)由于目前可用的数据有限,所以建立的模型较为简单,只考虑了松散层厚度、深厚比、倾角最主要的3个影响因素,而实际情况下,影响地表下沉系数的因素远远不止这3个,而建立更复杂、更逼近实际的模型则需要足够的样本为前提。应加大矿山开采沉陷的数据收集工作的力度,为研究沉陷机理控制开采沉陷,提供更丰富更完整的矿山沉陷数据。

[1]邹友峰,邓喀中,马伟民.矿山开采沉陷工程[M].徐州:中国矿业大学出版社,2003.

[2]彭林军,赵晓东,李术才.深部开采地表沉陷规律模拟研究[J].岩土力学,2011,32(6):1910-1914.

[3]Zhai Shuhua,Gao Qian,Song Jianguo.Genetic Programming Approach for Predicting Surface Subsidence Induced by Mining[J]. Journal of China University of Geosciences,2006,17(4):361-366.

[4]Kratzsch,H.Mining Subsidence Engineering[M].Berlin: Springer-Verlag,1983.

[5]Deng Jian,Bian Li,Li Xibing,etal.Analysisof factors and countermeasures of mining subsidence in Kaiyang phosphorus mine [J].Journal of central south university of technology,2006,13 (6):733-737.

[6]Cai Yinfei,Verdel Thierry,Deck Olivier.On the topography influence on subsidence due to horizontal underground mining using the influence function method[J].Computers and Geotechnics, 2014,61(1):328-340.

[7]杨治林.煤层地下开采地表沉陷预测的边值方法[J].岩土力学,2010,31(S1):232-236.

[8]LiWenxiu,Liu Lin,Dai Lanfang.Fuzzy probability measures (FPM)based non-symmetricmembership function:Engineering examples of ground subsidence due to underground mining[J]. Engineering Applications of Artificial Intelligence,2010,23(3): 420-431.

[9]Jiang Yan,ZhangYuzhuo,Song Zhenqi,et al.The new method of prediction on mining subsidence and deformation[J].Journal of Coal Science＆Engineering(China),2005,7(1):25-29.

[10]LiuBaochen.Ground surfacemovement due to underground excavation in P.R.china[M].In:Comprehensive Rock Engineering (Edited by JA Hudson).Pergamon Press,1993(4):781-817.

[11]郭文兵,邓喀中,邹友峰.地表下沉系数计算的人工神经网络方法研究[J].岩土工程学报,2003,23(2):212-215.

[12]何 晖,赵 敏,林开升.基于神经网络的地表下沉系数计算[J].有色金属,2004,56(3):90-93.

[13]Ambrozic T,Turk G.Prediction of subsidence due to underground mining by artificial neural networks[J].Computers＆Geosciences,2003,29(5):627-637.

[14]Deng Jian,Bian Li.Investigation and characterization ofmining subsidence in Kaiyang Phosphorus Mine[J].Journal of Central South University of Technology,2007,14(3):413-417.

[15]朱庆伟,蒋 军,张润安,等.大采高浅埋深煤层覆岩破坏规律数值模拟[J].煤炭工程,2013,(11):75-78.

[16]孙豁然,王述红,官永军等.大型地下硐室开挖过程位移变形智能预测[J].煤炭学报,2001,26(1):45-48.

[17]Unlu Tugrul,Akcin Hakan,Yilmaz Ozgur.An integrated approach for the prediction of subsidence for coalmining basins[J].Engineering Geology,2013,166:186-203.

[18]冯夏庭,朱维申.智能岩石力学在地下工程中的应用[J].岩石力学与工程学报,1999,18(z):822-825.

[19]罗 建.系统灵敏度理论导论[M].西安:西北工业大学出版社,1990.

[20]Jaiswal S,Benson ER,Bemard JC,et al.Neural Network Modelling and Sensitivity Analysis of a Mechanical Poultry Catching System[J].Biosystems Engineering,2005,92(1):59-68.

[21]Deng Jian,Gu DS,Li XB,Yue ZQ.Structural reliability analysis for implicit performance functions suing artificial neural network [J].Structural Safety,2005,25(1):25-48.

[22]国家煤炭局.建筑物水体、铁路及主要井巷柱留设与压煤开采规程[M].北京:煤炭工业出版社,2000:50-155.

2015-05-08)

刘 浪(1985-)，男，陕西靖边人，博士，从事采矿与安全系统工程方面的研究，Email:csuliulang＠163.com。

国家自然科学基金(51504182)；陕西省自然科学基金项目(2015JQ5187)；陕西省教育厅基金项目(15JK1466)；西安科技大学能源学院青年教工创新项目(2014-NY-018).