水平激励下钻井船矩形月池的水动力特性研究

黄 磊，刘利琴，唐友刚，张永恒，郭东杰

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 天津海事局，天津 300211)

水平激励下钻井船矩形月池的水动力特性研究

黄 磊1，刘利琴1，唐友刚1，张永恒1，郭东杰2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 天津海事局，天津 300211)

研究了具有矩形月池的钻井船在小幅水平横荡简谐运动激励下的辐射问题．利用简化的底部边界条件，基于线性势流理论建立了钻井船月池二维流体运动方程，利用Galerkin方法求得月池内流体速度势，得到月池对船舶的附加质量表达式．利用半解析解，研究了月池的水动力特性及月池参数对船舶水动力参数的影响．以边界元方法建立具有矩形月池结构的钻井船数值模型，数值模拟结果与半解析解进行对比验证．结果表明，在激励频率穿过月池内流体的固有振动频率时，附加质量会依次出现正、负峰值；自由液面及月池底部无量纲速度分布受激励频率及月池无量纲水深的影响较明显；在不同无量纲水深下，半解析解与数值模拟结果吻合较好．

月池；半解析解；附加质量；线性势流理论

船舶在水中受到波浪激励而产生的运动会引起辐射波对船体产生附加质量．附加质量体现了流场内流体对船舶的作用，是精确预报船舶水动力性能的重要参数之一．钻井船需要从甲板下放钻井立管等钻井及施工辅助设备，故设计时通常在船体中央布置自上而下贯穿整个船体的矩形井，其底部开放海水自由流动，上部为自由液面，称之为月池[1]．月池在为钻井设备提供下放通道的同时，也保护钻井施工免受水线面附近波浪力的影响．常见的类似钻井船月池的结构还有深水SPAR平台中央井，双体船及并靠船舶两船体间的狭长通道等．传统的船舶设计时仅考虑外部流场对船体的影响，不考虑月池内流体的影响，而月池排水量可达钻井船排水量的5%,以上，对船舶运动性能的影响不可忽略，因很多学者通过理论、试验及数值模拟等方法对月池进行了研究．

Albers[2]通过衰减实验测定了圆形月池的垂荡附加质量及附加阻尼，并研究了在月池内布置阻尼板对平台月池运动的影响．Sphaier等[3]通过模型实验测定了具有月池的单柱型结构的RAO曲线，研究了不同的底部开口面积对结构运动响应的影响．实验发现，月池内流体存在明显的动力学特性，对船舶的运动具有明显的影响．实验方法在模型、实验环境方面与实际情况最为相近，可较准确地预报船舶运动[4-5].但是保证船舶实验的精度对实验设备及测试系统具有较高要求，且实验周期较长，费用较高．

Mavrakos[6]和Zhou等[7]利用线性势流理论建立了圆形月池内流体的运动方程，利用域分解的方法得到了方程的半解析解，求解了结构的附加质量．朱仁传等[8]基于CFD理论，数值计算了不同振荡模态下浮体的附加质量与阻尼．Kristiansen等[9-11]基于流体动力学数值计算理论建立数值水池，进一步揭示了月池底部剪切层流动分离现象对船舶垂荡运动的影响.

对于横荡运动下月池的水动力特性目前研究较少．为进一步揭示月池内流体对船体水动力特性的影响，本文将基于线性势流理论，建立小幅横荡运动下矩形月池内流体的流体控制方程，求解速度势函数半解析解，推导附加质量的表达式，并利用边界元法验证半解析解结果．

1 数学模型建立

考虑二维矩形月池，其两侧壁之间的宽度为a，水深为h~，月池底部开放．建立平面坐标系Oy~z~，原点O位于月池底部中点．月池内速度势函数为．月池沿y~轴方向做频率为Ω、幅值为Y~0的小幅横荡简谐运动．选取适当的参数对系统进行无量纲化．选取a作为特征长度，特征时间取为1/Ω．各变量无量纲化后定义为

式中：Φ为无量纲速度势；g为重力加速度．变量无量纲化后，月池两侧壁间宽度为1，无量纲水深为h= h~/a，月池无量纲运动幅值为Y0=Y~0/a．由于月池做小幅度运动，Y0＜＜1．月池横荡位移为Y(t)=Y0eit.

无量纲后月池各参数如图1所示，其中Sd为月池一侧壁的湿表面面积，Sf为月池内自由表面面积，Sb为月池底面面积．

图1 无量纲矩形月池坐标系Fig.1Coordinates system of the nondimensional rectangular moonpool

假设月池内流体满足无黏、无旋、不可压缩的理想流体条件，根据线性势流理论，月池内流体无量纲速度势函数()y,z,tΦ满足连续方程[12]

月池在水平方向做小幅运动，在侧壁位置流体与月池壁具有相同速度，满足边界条件

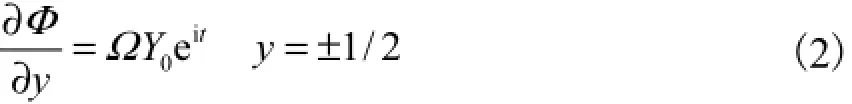
月池底部无底板，内外流体联通，考虑月池内、外流体的质量交换，采用Molin[13]提出的底部简化边界条件

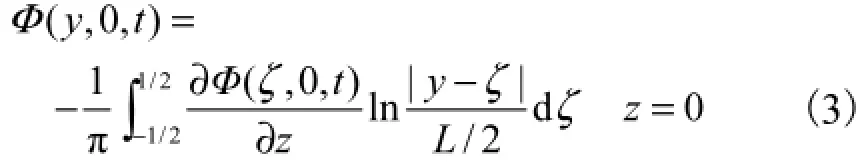
式中L为置于船体两侧的点汇距原点的距离，本文中取L＝4.5．月池液面满足线性化的自由液面条件

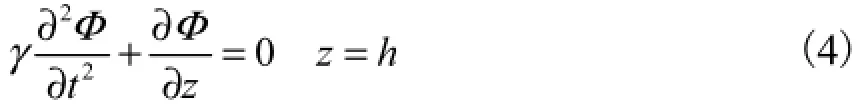
为求解方程及边界条件式(1)～式(4)，设Φ(y,z,t )有如下形式的解

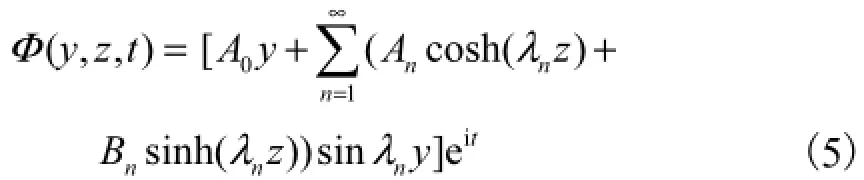
式中：A0、An(n=1,2,…)和Bn为待定系数；λn= (2n−1)π．

根据边界条件式(2)，有

故A0=Y0．此时，Φ(y,z,t) 满足式(1)及式(2)．将式(5)代入式(3)，得到

将式(7)代入式(6)得到

将式(8)两侧同乘sin(λmy)后，对y做−1/2～1/2积分，得到

式中

整理式(9)，得

式中

将式(5)代入自由液面条件式(4)，得

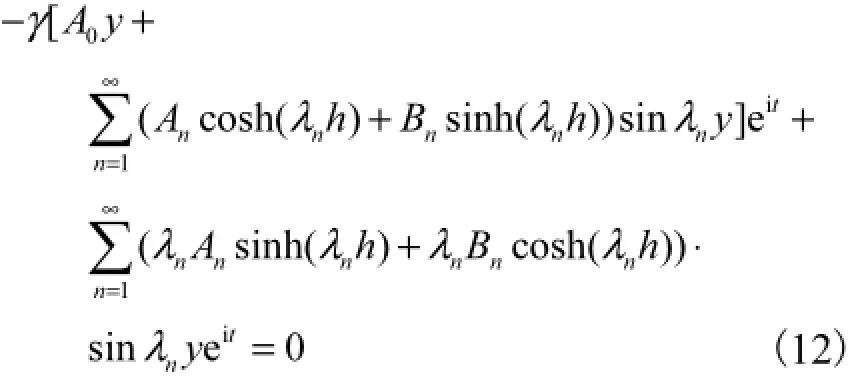
将式(7)代入式(12)，整理得

将式(13)改写为矩阵形式，即

式中

式中

确定Φ(y,z,t)后，可由伯努利方程确定月池内各点的动压力

式中ρ为流体密度．考虑所研究问题为月池小幅运动下的线性问题，略去方程(19)中的高次项，得到

对月池一侧的湿表面面积dS积分，得到月池水平小幅运动时，月池壁上的作用力

式中：u为单位外法向矢量；22A为月池小幅横荡运动时月池内的流体对结构的附加质量．考虑式(5)及式(20)，求得横荡运动时月池附加质量

2 半解析解验证分析

在役钻井船月池两侧壁间宽度多在10,m左右，本文选取钻井船Deepwater Pathfinder为研究对象，利用SESAM软件对该钻井船进行水动力性能计算，并将得到的数值模拟结果与本文半解析方法的结果进行对比．

Deepwater Pathfinder为第5代超深水钻井船，作业水深达3,000,m以上，其主要参数见表1．

表1 Deepwater Pathfinder主要参数Tab.1 Main parameters of Deepwater Pathfinder

SESAM软件是DNV开发的商用水动力计算软件，其核心是美国麻省理工学院开发的WAMIT，用于评估无航速浮体动力学性能．本文利用GeniE模块建立了钻井船面单元水动力模型，在HydroD中进行水动力性能的计算．Deepwater Pathfinder钻井船的计算模型见图2．

图2 Deepwater Pathfinder钻井船的计算模型Fig.2 Numerical model of Deepwater Pathfinder drilling unit

由于月池底部与外部流场联通，在应用SESAM进行计算时，计算结果是船体整体的附加质量．为得到月池内流体对船体的附加质量，应分别计算月池底部完全封闭和底部完全开放两种情况下的附加质量．月池附加质量系数为

式中：mf为月池横荡方向无量纲的附加质量系数；Ad1及Ad2分别为有、无月池时船体横荡方向的附加质量；Lm及Bm分别为月池的长度及宽度；hm为月池内水深，本文中hm取设计吃水．

图3给出了不同水深下月池的附加质量系数随激励频率的变化曲线．图3(a)是水深为设计吃水d＝13.0,m时附加质量系数的结果．由图3(a)可以看到，当激励频率较低时，月池的横荡附加质量系数约为0.8．随着激励频率的增大，激励频率会穿过月池的固有频率区域，此时月池内液体大幅晃动，导致附加质量系数激增，出现一个正峰值，而由于月池运动系统的低阻尼特性，响应运动相位迅速改变180°，附加质量系数出现一个负峰值．

对比图3中半解析解与数值模拟结果可以看到，两条曲线变化趋势相同，计算结果吻合较好．图3(b)和图3(c)分别为较低水位(mh＝8.5,m)和较高水位(hm＝16.0,m)时附加质量系数的结果，可以看到在这两种工况下，两条曲线始终保持一致．

在海洋波浪常见的周期3～12,s内，入射波浪频率在0.5～2.0,rad/s之间．SESAM软件与半解析法计算得到的共振频率区间基本一致，具有较高频率的入射波浪有可能引起月池内的流体共振，产生数倍于月池排水量的附加质量，影响钻井船的正常作业．

图3 附加质量系数随激励频率的变化曲线Fig.3Change curves of added mass coefficient with excitation frequency

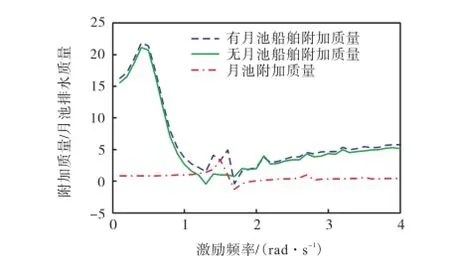
图4 附加质量与月池排水量的比值Fig.4Ratios of added mass to moonpool’s displacement

图4 给出了附加质量与月池排水质量的比值．其中，有月池和无月池船舶附加质量由SESAM软件计算而得，月池本身附加质量由本文方法计算而得．利用月池内流体的质量将附加质量无量纲化．由图4可以看到，对于具有月池的船舶，当波浪的频率接近月池的固有频率时，船舶横荡附加质量曲线中出现了第2峰值，是月池引起的；在月池的共振区域，月池的存在对船舶的水动力产生了明显的影响．

3 半解析解结果及分析

3.1 附加质量的收敛性

利用复化辛普生算法[14]，求解式(10)中二重积分的数值结果．计算得到矩阵H，其中H11=0.7737，H22=0.9312，H33=0.9593．

为实现式(22)中无穷项的求和，在保证收敛性的基础下，截取适当的有限阶次N．图5给出了无量纲月池附加质量的收敛性，可以看出各条曲线均已收敛，基本不再随截断阶次的增加而变化．这说明月池附加质量的半解析解有良好的收敛性．在计算中取N=4可以保证计算精度，且具有较高的计算效率．

图5 无量纲月池附加质量的收敛性Fig.5 Convergence of the nondimensional moonpool added mass

3.2 横荡附加质量

图6给出了不同h时无量纲月池附加质量随γ变化的曲线．由图中可以看到，在γ值较小时，附加质量随γ的增长变化较缓慢；随着γ的不断增大，月池附加质量出现了两个正峰值，每个正峰值后边伴随一个反向的峰，表明附加质量出现了较大的负值．随着γ的继续增加，附加质量又回到了正值．

由式(17)、式(18)及式(22)可知，当()+QHR为奇异矩阵时，解的表达式中出现奇点，此时若计算附加质量会得到无穷大的结果，此位置即为月池系统晃荡运动的共振位置．由图6可以看到γ的变化经过了月池系统的前两阶晃荡模态共振位置．

只保留矩阵中的主对角元素，通过简化可以求出月池各阶共振位置固有周期的近似结果，即

式中nnH为式(11)中矩阵H的主对角线上的元素11H和22H，由式(23)得到不同水深下一阶无量纲共振频

当γ接近共振位置时，月池内流体接近其晃动的固有频率nω，月池内波面响应的相位角会迅速变化180°，这意味着月池内流体波幅由与横荡加速度方向相反迅速改变为与其方向相同．此时，运动响应的方向与激励的方向同步，附加质量为负值，即在共振区域会出现以较小的激励幅值即可激励月池内流体的大幅运动的现象[15]．由图6还可以看到，1阶固有振动影响的范围要远大于2阶固有振动的影响范围．当γ在2～4之间时，附加质量都出现了明显的变化．而对于2阶模态，只在共振位置周围很小的范围内，月池的附加质量有变化．

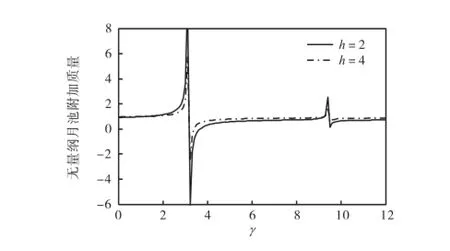
图6 无量纲月池附加质量随γ的变化Fig.6Changes of the nondimensional moonpool added mass with γ

图7 低频激励下的无量纲月池附加质量Fig.7Nondimensional added mass of moonpoolin low frequency excitation

图7 给出了γ在0～1.5的非共振区间变化时，不同水深h时无量纲月池附加质量随γ变化的曲线．由图中可以看到，对于h较小的月池，附加质量随γ的增长出现了由小变大的变化趋势．当h＝0.5，即月池的无量纲水深h与宽度比为1∶2时，γ由0.01增长到1.5，附加质量增长了约39%,．而随着月池无量纲水深h的增加，这种增长趋势逐步变缓．当h＝4.0时，月池的附加质量随γ的增长变化得比较平缓，基本上都维持在0.96～1.0左右．

月池内无量纲水深h的变化同样对横荡激励下的附加质量产生影响．图8给出了γ分别为0.5、1.0、2.0、2.5时，无量纲月池附加质量随h变化的曲线. 由图中可以看到，γ为0.5和1.0时，两条曲线变化规律基本相同．当1.0h＜时，即月池的水深小于月池的宽度时，无量纲月池附加质量随水深的增长而快速增长；当水深超过月池宽度时，曲线变得平缓，无量纲月池附加质量逐渐收敛在1.0左右．

图8 无量纲月池附加质量随h变化Fig.8 Changes of the nondimensional added mass of moonpool with h

横荡激励引起的月池内流体运动，主要是月池自由表面的晃荡运动．在远离共振区间的位置，月池自由液面做小幅晃荡运动．当月池内的水深较小时，月池内大部分的液体受到自由液面的影响，自由液面晃荡对月池的作用力在总的动压力中占了主要成分．然而自由液面的影响范围只局限在液面附近，随着水深的增长，液面晃荡的幅值减小，月池内流体的惯性力逐渐增加．当月池水深超过月池宽度时，流体的惯性力起主要作用，附加质量接近1.0．此时的附加质量基本为月池的排水量，月池带动全部流体随月池一同运动．

而观察图8中2.0γ=及2.5γ=两条曲线可以看到，与另两条曲线相比，这两条曲线有着明显不同的变化规律．由于振动频率已接近月池一阶的共振频率范围，月池中自由液面晃荡幅值增大．而随着水深的增加，月池内流体质量增加，惯性力逐渐增长，然而月池晃荡产生的作用力始终保持着较高的水平，在h＝0.7的位置达到峰值，此时自由液面及惯性力对附加质量的贡献量级相当．随着水深继续增加，液面产生的晃荡力相对于月池的排水量逐渐减小，曲线下降，但附加质量仍明显高于排水量．

对于常见的具有月池结构的船舶及海洋工程平台，例如钻井船、Spar平台等，月池宽度通常在10～20,m之间．在海洋工程环境中常见的波浪周期为3～15,s的入射波激励下，月池的γ值一般会在0.25～8.74之间．由图6可以看到，激励频率有可能经过月池一阶晃荡共振频率，因此在设计时要针对不同海况条件，选择合适的月池宽度．

若避开共振区间，对月池附加质量影响的主要因素是月池内的水深．当月池的水深大于月池的宽度时，月池内流体对船体的横荡附加质量基本等于月池的排水量；当月池的水深小于月池的宽度时，附加质量相对于水深变化明显，附加质量系数通常在0.5～1.0之间，需要针对不同的月池参数进行具体计算．

对于某些特定情况，γ值极易进入月池系统的共振范围．例如受到平台甲板上设备的高频激励，或者双体船两船体间狭长通道的纵荡运动，这些情况都可能使月池系统获得一个较大的γ值．此时月池内流体会出现剧烈的运动，其产生的附加质量可能会达到数倍月池排水量，甚至达到船体排水量的量级．对于此类情况，月池的存在会对船舶本身的运动产生明显的影响．

3.3 自由液面

根据速度势计算月池在自由液面位置的液面形状η/Y0．图9给出了h＝1.0时不同激励频率下的月池自由液面曲线，其中η为月池自由液面变化的高度．由图9可以看到，当γ＝3.2时，月池系统接近1阶晃荡共振区域，无量纲自由液面运动幅值明显增高.

图9 月池自由液面曲线(h＝1.0)Fig.9 Free surface curves of moonpool(h＝1.0)

图10 给出了在共振位置附近，γ分别为1.0、4.0、5.0时的月池自由液面曲线．相比与其他两条曲线，4.0γ=的曲线离共振位置更近，因此自由液面运动幅值更高．观察γ 为1.0、5.0的两条曲线可以看到，由于离共振位置距离基本相同，两条曲线的运动幅值相近，但液面形状有着较大的差别．5.0γ=时激励频率较高，液面呈现出正弦曲线的特征；而当1γ=.0时，激励频率低，液面形状基本为平面，以中点为中心摆动．

图10 月池自由液面曲线(h＝0.5)Fig.10 Free surface curves of moonpool(h＝0.5)

3.4 月池底部流体速度及压力

由于月池底部开放，月池底部位置流体的法向速度不为零．利用本文的半解析解，计算不同水深和频率时月池底部的无量纲切向速度vT=vT′/Y˙及无量纲法向速度vN=，如图11所示．其中v′T为月池底部的切向速度，v′N为月池底部的法向速度，Y˙为横荡激励的速度．

由图11可以看到，在月池侧壁的位置，不同的激励频率无量纲切向速度均为1，即流体的切向速度等于船体横荡激励的速度，这与边界条件(2)是一致的．稍远离侧壁后，切向速度比较稳定地保持在0.45左右．而无量纲法向速度则以月池的中点为中心反对称，一侧流体流进，一侧流出．在靠近侧壁的位置无量纲法向速度最大，在中心位置无量纲法向速度为零．

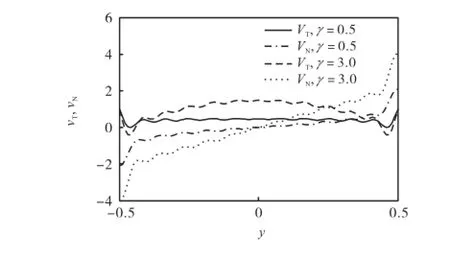
图11 月池底部无量纲切向及法向速度(1.0h=)Fig.11 Nondimensional tangential and normal velocities at bottom of moonpool(1.0h=)

对比图11中3.0γ=及0.5γ=时月池底部无量纲法向及切向速度可以看到，由于3.0γ=时接近月池的一阶共振位置，底部的无量纲切向和法向速度都明显升高．这是由于在共振位置自由液面产生了较大幅值的晃荡，而月池水深较小，液面的运动带动了底部流体流动，底部流速变大．

图12给出了3.0γ=时不同水深时月池底部无量纲法向速度．由图中可以看到，月池底面离自由液面越近，对速度的影响越大，无量纲法向速度明显增加.当月池水深达到宽度的1.5倍时，这种影响基本消失.

图12 月池底部无量纲法向速度(γ＝3.0)Fig.12Nondimensional normal velocity at the bottom of moonpool(γ＝3.0)

图13 和图14给出了在月池底部0z=位置的无量纲压力．由图13中曲线可以看到，月池底部位置的压力在中间最小(等于0)，两侧靠近月池侧壁的位置最大．在月池两侧壁位置的无量纲压力大小相等，方向相反．无量纲压力在两侧壁间基本呈反对称的线性分布．对比各曲线可以看到当水深同为1.0，γ分别为0.1与0.5时，无量纲压力分布并无太大区别．而水深减小为0.1时，底部位置的压力明显减小．这说明水深对底部位置的无量纲压力影响较大，而γ的变化并不会明显影响无量纲压力分布．但是，当γ逐渐变化到接近月池固有振动频率时，会对底部位置的无量纲压力产生明显的影响．

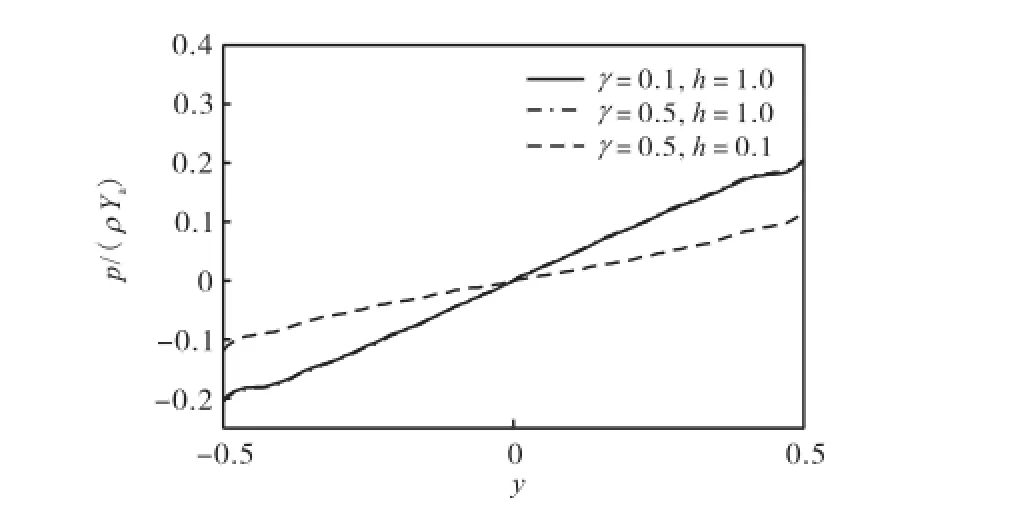
图13 月池底部无量纲压力Fig.13 Nondimensional pressure at the bottom of moonpool

由图14可以看到，当γ取3.18，即达到月池的1阶共振位置时，与相同水深γ＝1.0的曲线相比，达到共振时底部无量纲压力明显增大，压力的分布不再为线性增长，而是呈现出余弦曲线的形状，这是月池一阶共振振型的形式．

4 结 论

(1) 当激励频率接近月池共振频率时，会引起月池内流体大幅的晃动，响应运动的相位会迅速改变180°，从而与激励运动同相位．当月池内流体质量较大时，月池产生的负附加质量会极大地抵消船舶的质量，使船舶在同样幅度的激励下产生大幅的运动．

(2) 当月池内流体的水深小于月池宽度时，附加质量随水深变化明显．水深增长时，附加质量也会明显增长．当月池水深超过月池宽度时，这种变化规律不再明显．在非共振区域，月池底部的压力沿月池底部基本呈线性分布，月池中心位置压力为零，左右反对称分布．在共振区域，无量纲压力明显增大，沿月池底部分布呈现出共振模态振型．

(3) 通过与边界元分析得到的数值结果进行对比发现，本文提出的半解析方法能够给出正确的月池横荡附加质量．在常见的入射波浪的周期范围内，月池受横荡激励可能产生共振．共振时月池内自由液面出现较大幅的晃荡，产生数倍于月池内流体质量的正、负附加质量．若月池内流体的质量达到总排水量的30%,，共振时月池内流体附加质量对结构的运动会产生极大的影响．

［1］ Veer R V，Tholen H J. Added resistance of moonpools in calm water[C]//Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering. Estoril，Portugal，2008：57246.

［2］ Albers A. The water motions in a moonpool[J]. Ocean Engineering，1984，11(6)：557-579.

［3］ Sphaier S，Torres F，Masetti I，et al. Monocolumn behavior in waves：Experimental analysis[J]. Ocean Engineering，2007，34(11)：1724-1733.

［4］ Yang J C，Marks C H，Jiang J，et al. Determination of fluid damping using random excitation[J]. Journal of Energy Resources Technology，1985，107(2)：220-225.

［5］ An S，Faltinsen O M. An experimental and numerical study of heave added mass and damping of horizontally submerged and perforated rectangular plates[J]. Journal of Fluids and Structures，2013，39：87-101.

［6］ Mavrakos S A. Hydrodynamic coefficients in heave of two concentric surface-piercing truncated circular cylinders[J]. Applied Ocean Research，2005，26(3)：84-97.

［7］ Zhou H W，Zhang H S. Radiation and diffraction analysis of a cylindrical body with a moon pool[J]. Journal of Hydrodynamics，Ser B，2013，25(2)：196-204.

［8］ 朱仁传，郭海强，缪国平，等. 一种基于CFD 理论船舶附加质量与阻尼的计算方法[J]. 上海交通大学学报，2009，43(2)：198-203. Zhu Renchuan，Guo Haiqiang，Miao Guoping，et al. A computational method for evaluation of added mass and damping of ship based on CFD theory[J]. Journal of Shanghai Jiaotong University，2009，43(2)：198-203(in Chinese).

［9］ Kristiansen T，Faltinsen O M. Application of a vortex tracking method to the piston-like behaviour in a semientrained vertical gap[J]. Applied Ocean Research，2008，30(1)：1-16.

［10］ Kristiansen T，Faltinsen O M. A two-dimensional numerical and experimental study of resonant coupled ship and piston-mode motion[J]. Applied Ocean Research，2010，32(2)：158-176.

［11］ Kristiansen T，Faltinsen O M. Gap resonance analyzed by a new domain-decomposition method combining potential and viscous flow draft[J]. Applied Ocean Research，2012，34(1)：198-208.

［12］ Newman J N. Marine Hydrodynamics[M]. Massachusetts：The MIT Press，1977.

［13］ Molin B. On the piston and sloshing modes in moonpools[J]. Journal of Fluid Mechanics，2001，430：27-50.

［14］ 翟瑞彩，谢伟松. 数值分析[M]. 天津：天津大学出版社，2000. Zhai Ruicai，Xie Weisong. Numerical Analysis[M]. Tianjin：Tianjin University Press，2000(in Chinese).

［15］ Faltinsen O M. Sea Loads on Ships and Offshore Structures[M]. Cambridge：Cambridge University Press，1993.

(责任编辑：樊素英)

Hydrodynamic Characteristics of Rectangular Moonpool of Drilling Unit Under Horizontal Excitation

Huang Lei1，Liu Liqin1，Tang Yougang1，Zhang Yongheng1，Guo Dongjie2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. Tianjin Maritime Safety Administration，Tianjin 300211，China)

A study was carried out on radiation problem of a drilling unit with a rectangular moonpool under low amplitude horizontal harmonic excitation. The two-dimensional governing equations of the fluid in the moonpool were established based on linear potential theory. The simplified boundary condition was adopted. The fluid velocity potential and the added mass expression of the moonpool was solved by the Galerkin method. The hydrodynamic characteristics of the moonpool were studied and the effect of the moonpool parameters on the drilling unit was revealed. A numerical model of a drilling unit with a rectangular moonpool was built by boundary element method. The results of two methods were compared to verify the semi-analytical solution. The results show that the added mass presents positive and negative peaks when the excitation frequency passes through the natural frequency of the moonpool;the free surface shape and nondimensional velocity distribution are significantly affected by the excitation frequency and the non-dimensional draught of moonpool; the semi-analytical solution fits the numerical result well for different nondimensional draughts of moonpool.

moonpool；semi-analytical solution；added mass；linear potential theory

P751

A

0493-2137(2015)11-1001-08

10.11784/tdxbz201402029

2014-02-21；

2014-10-19.

国家自然科学基金资助项目(51179125).

黄 磊（1981— ），男，博士，leihuang@tju.edu.cn.

刘利琴，liuliqin@tju.edu.cn.