小样本下基于贝叶斯空间估计的故障诊断算法
闫治宇
摘 要:针对小样本下系统故障诊断问题,提出一种基于贝叶斯空间估计与主元分析(Principal Component Analysis, PCA)相结合的方法。首先运用主元分析离线建立(Squard Prediction Error)统计量阈值和故障模式特征向量矩阵库,然后在小样本情况下通过利用故障先验信息,采用吉布斯抽样(Gibbs Sampling, GS)提取数据特征向量矩阵,再利用与故障模式特征向量矩阵的相似性,完成故障诊断。实验结果表明了此方法的有效性。
关键词:主元分析 故障诊断 小样本 吉布斯抽样 矩阵相似性
中图分类号:TP391 文献标识码:A 文章编号:1674-098X(2015)03(c)-0059-02
随着科学技术的飞速发展,自动控制系统的规模越来越大,相应地也增加了系统复杂性,一旦系统发生故障将会给人们的生命安全带来巨大的危害[1],因此,提高系统的安全性和可靠性至关重要。而现如今大多数故障诊断方法都是在大样本数据下进行的[2],未考虑小样本时方法的有效性,因而解决实际中有时受环境影响只能得到小样本数据时的故障诊断问题具有很大的研究意义。
1 算法设计
针对小样本情况下系统故障检测和诊断的算法设计分为两个阶段:算法提出和算法验证。算法提出:我们发现基于贝叶斯主元模型与PCA主元模型一致,因此提出将两种方法相结合用于小样本情况下系统的故障检测和诊断;故障检测统计量采用统计量[3],故障特征向量矩阵表征了故障发生时所有变量的变化方向[4],可以利用特征向量矩阵相似性进行故障诊断。算法设计:首先根据先验信息利用PCA建立故障检测阈值和故障特征向量矩阵库,再利用基于贝叶斯空间估计完成在线测量数据的主元特征向量矩阵提取,然后利用统计量来实现故障检测,利用故障特征向量矩阵相似性实现故障诊断[5]。
2 算法实现
按上述算法设计离线建立故障检测阈值与故障库,当检测出系统发生故障时,由于受一定的环境影响所得样本数目少,这时就无法构成稳定的协方差矩阵,为解决这个问题,本文提出利用基于贝叶斯空间估计的方法提取特征向量矩阵,特征向量矩阵可由贝叶斯后验分布求得[6],如式(1)可得:
(1)
其中,,可根据信噪比得到,即,为数据矩阵标准化矩阵。
基于上述条件,利用下述算法可计算矩阵,为随机抽样所得特征向量矩阵。
输入:任意初始变量
1:for do
2:由式(1),通过GS得
3:end for
由上述一序列随机抽样矩阵,可得估计特征向量矩阵,其中为取括号内矩阵的个主元向量。
根据上述步骤可得小样本数据的特征向量矩阵。
本文采用特征向量矩阵相似性实现故障诊断,矩阵相似性如式(2)所示
(2)
其中,式(2)中的为加权系数,用以强调不同投影方向的不同重要性。满足,并且。所以,式(2)的值越接近1,表明两个矩阵的相似度越高[6]。
根据以上给出的算法步骤,求得估计的特征向量矩阵与已知故障模式特征向量矩阵相的似性,确定故障模式完成故障诊断。
3 仿真验证
取,,,,,;通过取所加故障时刻的前后时刻样本数,作为小样本数目。可得故障诊断结果如下:
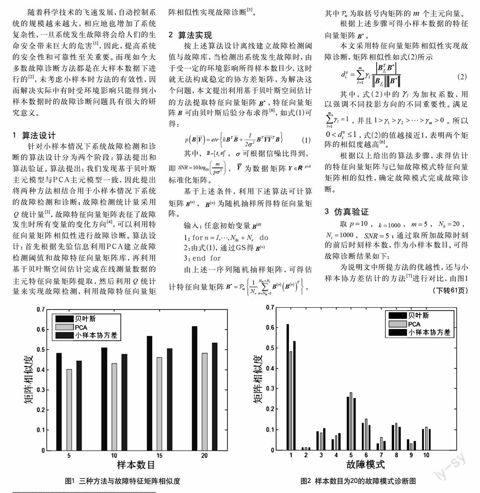
为说明文中所提方法的優越性,还与小样本协方差估计的方法[7]进行对比,由图1可以看出在小样本情况下,基于贝叶斯空间估计方法的矩阵相似度明显高于PCA、小样本协方差估计方法的矩阵相似度。图2为三种方法所提取特征向量矩阵与故障库中的10种不同故障模式特征向量矩阵的相似度,由图可以看出只有基于贝叶斯空间估计所提取的特征向量矩阵与故障第一类模式的相似度最大,也验证了与实验所取第一类故障样本数据相吻合,从而此方法可实现小样本下系统的故障诊断。
4 结论
该文提出了一种将基于贝叶斯空间估计和PCA相结合的方法用于小样本情况下故障诊断,根据发生不同的故障对应不同的特征向量矩阵,采用特征向量矩阵相似性来实现故障诊断。实验结果验证了此方法在小样本情况下故障诊断的优越性。
参考文献
[1] 周东华,叶银忠.现代故障诊断与容错控制[M].北京:清华大学出版社,2000.
[2] 阳宪惠,张杰.多变量统计过程控制[M].北京:化学工业出版社,2000.
[3] 邱宗江,刘慧霞,席庆彪,肖佳伟.无人机PCA故障检测与诊断技术研究[J].计算机工程与应用,2013,04:262-266.
[4] 郭明,王树青.基于特征子空间的系统性能监控与工况识别[J].化工学报,2004, 55(1):151-154.
[5] 王姝.基于数据的间歇过程故障诊断及预测方法研究[D].东北大学,2010.
[6] Besson O, Dobigeon N, Tourneret J Y. Bayesian Estimation of a Subspace [J].Signals Systems and Computers. IEEE, 2011, PP: 629-633.
[7] Tadjudin S,Landgrebe D A. Covariance Estimation for Limited Training Samples[C]. Geoscience and Remote Sensing Symposium Proceedings, IEEE International. 1998, 5: 2688-2690.