基于SLBH 特征的行人检测算法研究
张祎蔚


摘要:受韦伯局部描述子和LBP特征的启发,针对Haar特征维度高、冗余度大以及对光照变化适应性差等缺点,提出了一种于显著性的局部二值化Haar特征。首先将8种Haar特征组合形成一个3*3的块,利用局部二值化思想得到二值化Haar特征;然后根据韦伯定律求取该块的显著性因子;最后把显著性因子作为权重将二值化Haar特征统计成直方图而得到SLBH特征。通过在INRIA行人样本库上实验,表明该特征具有较好的鲁棒性、较高的检测率和较低的虚警率。
关键词:韦伯局部描述子;LBP特征;SLBH特征;显著性因子;行人检测
中图分类号:TP18 文献标识码:A 文章编号:1009-3044(2015)09-0202-03
近年来,基于计算机视觉的行人检测技术一直是智能交通系统领域研究的热点问题[1],而可行且高效的行人特征提取算法是其中的关键部分,为此,许多专家学者对此进行了深入研究。
Haar特征由Viola等学者首次提出并用于人脸识别领域,取得了良好的检测效果[2,3],而后被许多学者改进和扩展,使其更加适合于行人检测领域。Abramson Y[4]在标准haar特征的基础上进行了扩展,以增强对运动行人姿态的描述和检测。但该特征仍然易受光照变化、环境遮挡等因素的影响,适应场景变化的能力较差,鲁棒性不高。HOG特征是行人检测特征提取领域的另一经典算法,与haar特征不同,HOG特征属于矢量特征范畴[5]。Lazebnik S等人[6]为了提升了HOG特征提取速度提出了PHOG特征。SIFT特征[7]由于其优异的不变性也被广泛到应用到目标检测特征提取的应用中。HOG特征和SIFT特征都是比较典型的矢量特征提取算法,但是由于特征维数较高,实时性难以保证,必须经过特征降维处理。再就是Edgelet特征[8-9],与其他行人检测特征提取算法不同,该特征着力于描述行人轮廓特征,能有效处理环境复杂且目标被遮挡情况较为严重条件下的行人检测,但是由于计算较为复杂,实时性较低。Ojala T等人提出的LBP特征因其具有维度低、计算速度快、能很好的刻画图像的纹理信息而被广泛应用,并且出现了许多的变体[10,11]。Chen等人[12]根据韦伯定理提出了韦伯局部描述算子,该特征虽然对光照和噪声干扰具有一定的鲁棒性,但是其特征提取仍比较复杂,计算量较大。
本文在分析上述特征的基础上,针对Haar特征维度高、冗余度大,而LBP特征又无法刻画人眼的视觉敏感度,提出了一种基于显著性的局部二值化Haar特征(Saliency Local Binary Haar,SLBH)提取算法。该特征维度低,对平移、缩放和噪声具有一定的鲁棒性,并能显现特征的局部显著性,从而提高了行人检测的准确率。本文结构安排如下:SLBH特征将在第2节详细介绍,第3节给出实验与结果分析,最后是总结。
1 SLBH特征
1.1 显著性因子
显著因子是对局部特征显著性的描述,韦伯定律指出,在发散的局部特征中,局部显著性不能由差别阈限的绝对值来进行比较,而应由其相对值进行确定。根据韦伯定律[12],可以利用式(1)计算出中心像素点在其邻域内的显著性因子。其中[Ic]表示中心像素点的灰度值,p为邻域个数,[Ii]为对应邻域像素点的灰度值。
[S(Ic)=arctani=0p(Ii-Ic)Ic] (1)
其中,[S(Ic)∈-π2,π2]。 为了方便后续计算,本文再通过增加一个值为[π2]的偏置项将[S(Ic)]值域转换至转换[0,π]。[S(Ic)]是对局部特征显著性的描述,其值越大表明显著性越强。
1.2 加权LBP特征
局部二元模式(LBP)是一种描述图像局部纹理的算子,因其具有计算简单,对光照变化不敏感等优点而被广泛应用于计算机视觉领域。LBP特征计算如式(2)所示,其中[gc]为中心像素点的灰度值,[gi]为[gc]的八个邻域像素点灰度值,[s(?)]为阈值比较函数,其定义如式(3)所示。
[LBP(gc)=i=07s(gi-gc)?2i] (2)
[s(x,y)=0,if x-y≤T1,otherwise] (3)
在计算出整幅图像的LBP特征值后,根据式(4)统计LBP特征直方图,其中判断函数[f(?)]定义如式(5)所示。
[H(k)=x,yf(LBP(x,y),k),k∈[0,K]] (4)
[ f(x,y)=1,if x=y0,otherwise] (5)
LBP特征仅利用了中心像素与其邻域内像素间的差异,而缺乏对物体显著性的描述。如图1所示,虽然两个矩形区域具有相同LBP特征值,但是其显著性因子相差却很大。根据韦伯定律,显著因子越大,其顯著性越强,其所描述的信息也就越重要,而LBP特征并不能描述这些显著性信息。Cao Y等人[11]利用中心像素与邻域像素差的绝对值之和作为权值,来增加像素间差异在LBP特征直方图中的影响,如式(6)所示,其中K为最大的LBP特征值,判断函数与式(5)相同,权值函数如式(7)所示。
[H(k)=x,yw(x,y)*f(LBP(x,y),k),k∈[0,K]] (6)
[w(gc)=i=07|gi-gc|] (7)
Cao Y等提出的加权LBP直方图虽然考虑到了像素邻域间差异的影响,但是它也没能很好描述特征的局部显著性。此外,由于在加权直方图统计过程中不断累积权重,使得各维度之间相差较大。受韦伯定理的启发,本文使用更接近人类视觉差异的显著性因子作为权重来统计加权LBP直方图。直方图统计函数如下:
[H(k)=x,yS(x,y)*f(LBP(x,y),k),k∈[0,K]] (8)
1.3 SLBH特征
Viola等人[3]最先提出并將Haar特征应用于行人检测中。但随着研究的深入,学者们发现原始的Haar特征对于检测静止的、对称的物体比较有效,而对于行人这类非刚性物体,则需要在其它方向上增加能够描述行人运动特点的特征。Lienhart R等人在Viola提出的标准Haar特征的基础上进行了扩展,本文使用了图2所示的这8种扩展的Haar特征。
将上述8种Haar特征构成了一个3*3的矩形区域,为了方便描述,我们称Haar特征的黑色或者白色矩形区域为一个cell,而3*3的矩形区域称为一个block。如果对3*3区域从上到下,顺时针编号,分别表示为[c0],[c1], [c2], [c3], [c4], [c5], [c6],[c7], 中心黑色区域表示为[cc],如图3所示。然后按照式(1)进行计算,得到的结果为局部二值化Haar特征(Local Binary Haar,LBH)。
其中,[I(k,l)]表示图像[I]在点[(k,l)]处像素值,w表示cell的宽度,h表示cell的高度。考虑到LBP模式缺乏对显著性描述的缺陷,因此本文利用式(8)来统计局部二值化Haar特征直方图,即SLBH特征。该特征计算步骤如下:
Step 1:将输入图像转换到灰度空间。
Step 2:利用积分图技术求取每个cell的像素灰度值之和。
Step 3:将8个cell按照图3所示结构组成一个block。
Step 4:根据式(9)计算每个block内的LBH值,根据式(1)计算每个block的显著性因子。
Step 5:按照式(8)统计直方图,即为该图像的SLBH特征。
与传统Haar特征相比,SLBH特征增加了显著性因子计算,其计算复杂度虽高于传统Haar特征,但该特征在刻画行人纹理信息时需要的特征数量较少,故此特征实时性较好。由于引入加权局部二元模式的思想使SLBH特征拥有传统的Haar特征无法比拟的光照不变性,可以有效的提高系统的鲁棒性,这在下面的试验中可以看到SLBH特征优越的检测效果。
2 实验与结果分析
为了验证本文算法的有效性与优越性,设计了两组实验进行特征性能评估和检测性能对比。所有的实验样本均采集于INRIA行人样本库,其中训练集中正样本2416幅行人图像,负样本为3070幅,测试集中正样本1126幅,负样本3070幅。图4为本文算法的实现流程图。为了能够直观的显示出各种特征的检测性能,本文使用检测率(detection rate, DR)、虚警率(False Positive Rate, FPR)和识别率(recognize rate, RR)以及平均每幅图像特征提取时间(Average Extraction Cost, AEC)4种评价指标,其计算公式如式(11)、式(12)和式(13)所示。其中TP表示行人检测为行人(true positive),FP表示是非行人检测为行人(false positive),FN表示行人检测为非行人(false negative)。
2.1特征性能评估
为了测试本文对Haar特征改进的性能,实验选用了Haar、LBH和SLBH特征做对比实验,并且选择SVM作为分类器。实验统计结果如表1所示,从表1中可以发现本文提出的SLBH特征虽然特征提取时间略高于其它两种特征,但是在其它3种评价指标上都优于Haar和LBH特征。
2.2 检测性能对比
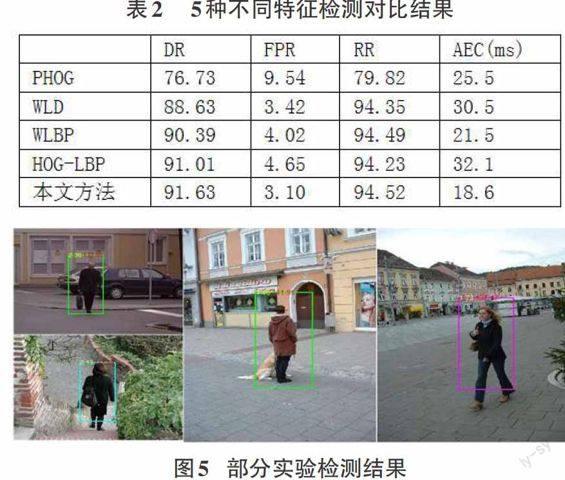
本文在相同的实验条件下选择PHOG特征[6]、加权LBP特征[11]、WLD特征[12]、HOG-LBP特征[13]和本文算法进行对比实验。其实验结果如表2所示,可以看出,本文提出的SLBH特征的各项评价指标均高于其它方法的实验效果。图5是在Detect Human行人样本测试集上测试的部分实验结果图。
3 总结
本文针对Haar特征维度高、冗余大以及对光照敏感等不足提出了一种显著性的局部二值化Haar特征,该特征结合了视觉显著性和加权LBP的思想,能减少Haar特征的维数,并增强了纹理描述能力。通过在INRIA行人样本库中实验,结果表明本文所提方法的检测率与误检率都优于其它方法。
参考文献:
[1] Dollar P, Wojek C, Schiele B, et al. Pedestrian detection: An evaluation of the state of the art[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2012, 34(4): 743-761.
[2] Viola P., Jones M. Robust real-time face detection [J]. International Journal of Computer Vision, 2004, 52(2):137-154.
[3] Viola P, Jones MJ, Snow D. Detecting pedestrians using patterns of motion and appearance [J]. International Journal of Computer Vision, 2005, 63(2):153-161.
[4]Abramson Y., Rabinovich A..Decidability of split equivalence [J].Information and Computation,2002,173(1):15-39.
[5]Pang Yanwei, Yuan Yuan, Li Xuelong, Pan Jing.Efficient HOG human detection [J].Signal Processing,2011.91(4):773-781.
[6]Lazebnik S,Schmid C,Ponce J.Beyond Bags of Features:Spatial Pyramid Matching for Recognizing Natural Scene Categories [C]//Prac of the IEEE Computer Seciety Conference on Computer Vision and Pattern Recognition, 2006:2169-2178.
[7]Lowe D M.. Distinctive image features from scale-invariant keypoints [J]. International Journal of Computer Vision, 2004, 60(2):91-110.
[8]Wu Bo, Nevatia Ram.Detection and tracking of multiple, partially occluded humans by Bayesian combination of edgelet based part detectors [J].International Journal of Computer Vision,2007,75(2):247-266
[9]Hu Bin, Wang Shengjin, Ding Xiaoqing.Multi features combination for pedestrian detection [J].Journal of Multimedia,2010,5(1):79-84
[10]Thanh Nguyen D, Ogunbona P O, Li W. A novel shape-based non-redundant local binary pattern descriptor for object detection[J]. Pattern Recognition, 2013,46(5):1485-1500.
[11]Cao Y, Pranata S, Nishimura H. Local Binary Pattern features for pedestrian detection at night/dark environment[C]//18th IEEE International Conference on. IEEE, 2011: 2053-2056.
[12] Chen J, Shan S, He C, et al. WLD: A robust local image descriptor[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2010,32(9):1705-1720.
[13]Gan G, Cheng J. Pedestrian detection based on hog-lbp feature[C]//Computational Intelligence and Security (CIS), 2011 Seventh International Conference on. IEEE, 2011: 1184-1187.

