电力机车牵引变压器副边绕组过电压计算
何建
(南车株洲电机有限公司 牵引变压器研发部,湖南株洲412001)
电力机车牵引变压器副边绕组过电压计算
何建
(南车株洲电机有限公司 牵引变压器研发部,湖南株洲412001)
为了研究计算电力机车牵引变压器在暂态过电压作用下副边绕组的电压响应问题,从电力机车牵引变压器原、副边绕组的电压传递函数出发,分别计算了牵引变压器的谐振频率点和副边绕组在暂态过电压作用下的响应。首先测量出机车牵引变压器原、副边绕组的电压传递函数,并用矢量匹配法和Arnoldi算法对此电压传递函数进行有理函数逼近和降阶处理,然后计算电压传递函数的谐振频率点。运用电网络理论得到传递函数的高频无源电路模型,此模型是一个由无源元件R,L,C和理想变压器组成的二端口网络。最后通过对此二端口网络施加不同类型的暂态过电压,仿真计算了变压器副边绕组的电压响应。
电力机车牵引变压器;传递函数;高频电路模型;暂态过电压
车载牵引供电系统是电力机车的核心装备,其中牵引变压器是此系统的核心部件之一,其运行可靠性直接关系到铁路运输的安全与畅通。电力机车由受电弓从铁路沿线的接触网获得电能,电能通过变换后由牵引电机驱动机车[1]。中国中西部地区地域空旷,铁路网附近的落地雷会在接触线上形成感应雷过电压,而且铁路沿线隔离开关以及断路器的操作也会产生大量暂态过电压并沿接触线侵入牵引变压器高压绕组。这些外部和内部的过电压幅值大小不一,频率分布范围广。一些特殊频率的过电压其幅值不会造成牵引变压器一次绕组的击穿,但会在副边绕组上产生严重的过电压而危害其绝缘安全。
通过对一台机车牵引变压器传递函数的测量和计算,得到了使副边绕组产生过电压的谐振频率。用矢量匹配对测量的传递函数进行有理函数逼近,然后通过Arnoldi算法得到降阶后的传递函数,最后用电网络理论建立起了传递函数的高频电路模型。对此二端口模型施加不同类型的激励源仿真计算了牵引变压器副边绕组的过电压响应。
1 传递函数的测量与谐振点的计算
1.1 电压传递函数的测量
本文用网络分析仪对1台TBQ 32-5280/25的牵引变压器高、低压绕组之间的电压传递函数进行测量,变压器的基本参数见表1。
该机车牵引变压器是一台多绕组单相变压器,有4个高压绕组和4个低压绕组,各绕组之间要求解耦布置。4个高压绕组并联运行,4个低压绕组分别单独运行供电,高低压绕组之间电压传递函数的测量示意图如图1所示,试验现场见图2所示。
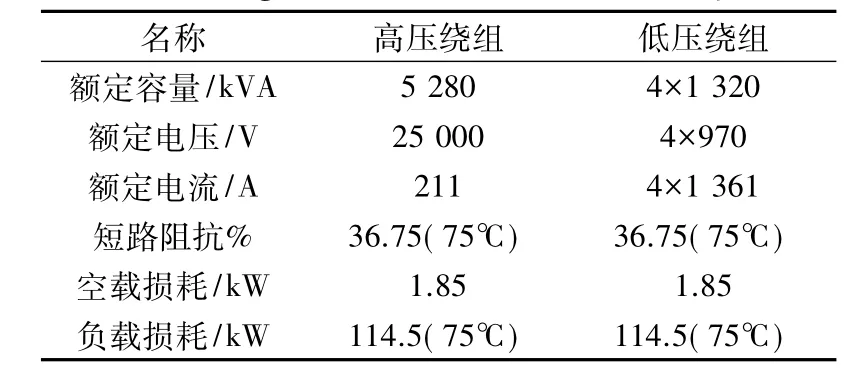
表1 TBQ 32-5280/25变压器的额定参数

图1 试验测量示意图
分析仪测量了低压绕组(LV2,LV3,LV4)在开路的情况下高压绕组HV对低压绕组LV1的电压传递函数,测量结果见图3和图4所示。
1.2 谐振频率点的计算
分析传递函数的辐频曲线可以得知,在频率较低(f<44 kHz)的范围内传递函数幅值的大小基本和高低压绕组之间的变比(n=0.038 8)相当,而当频率较高时则发生了明显的谐振。对测量数据进行处理计算后得到低压绕组的谐振频率分布范围(幅值比>0.15)约为: 169 kHz至231 kHz,其中以177.83 kHz和199.98 kHz两个频率点的谐振幅值最高,分别达到了0.264 7和0.292 2。在频率为445 kHz处也有一个较小的谐振其幅值为0.123。

图2 测量试验现场

图3 传递函数的幅频曲线

图4 传递函数的相频曲线
2 传递函数的降阶处理和高频电路模型
用矢量匹配对测量的传递函数进行曲线拟合,矢量匹配算法是一种稳定、有效的拟合方法。它采用一阶有理分式和的形式来拟合传递函数的有理函数表达式f(s),其部分分式和的形式为:式中留数cn和极点pn是实数或者是共轭复数对,参数d和e是实数,N是拟合的阶数[2]。
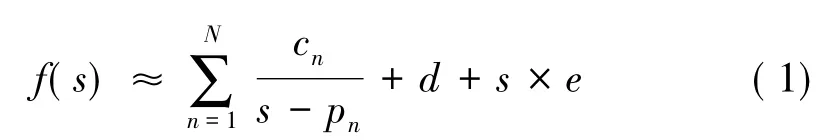
对传递函数进行矢量匹配拟合后的阶数为80阶,包括2个实数极点和39对共轭复数极点。匹配后的辐频曲线和相频曲线见图5和图6。

图5 匹配后传递函数的幅频曲线(80阶)

图6 匹配后传递函数的相频曲线(80阶)
2.1 传递函数的降阶
初始匹配后的电压传递函数阶数较高,这样建立起来的高频电路模型较为复杂。通过把矢量匹配计算出来的传递函数转化为状态方程后[3],用Arnoldi算法[4]对此高阶电压传递函数进行降阶得到降阶后的传递函数。降阶前后传递函数的辐频曲线和相频曲线对比见图7和图8所示。

图7 降阶后的幅频曲线
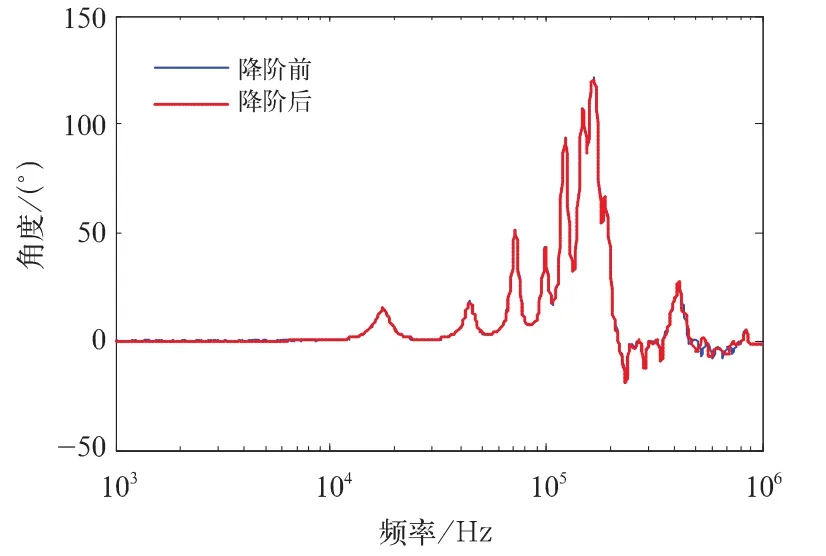
图8 降阶后的相频曲线
通过对比分析降阶前后的传递函数曲线可以得知,用Arnoldi降阶算法得到的低阶模型对系统原有的传递特性改变很小,并且保证了传递函数的稳定性和无源性。
传递函数降阶后的阶数为50阶,包括2个实数极点和24对共轭复数极点,其极点和留数的数值见表2所示,表中只列出实数极点和虚部为正数的共轭复数极点。

表2 降阶后电压传递函数的参数值
2.2 高频电路模型
基于降阶之后的传递函数,运用电网络理论得到降阶传递函数的高频电路模型[5]。
(1)对于实数极点组成的有理函数分式:
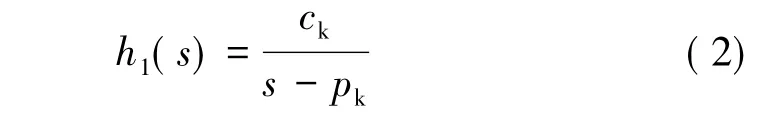
其对应的电路模型如图9所示。

图9 h1(s)对应的电路模型
其中 ,L1k=-1/pk,n1k=-ck/pk。
(2)对于共轭复数极点组成的有理函数分式:

其对应的电路模型如图10所示。
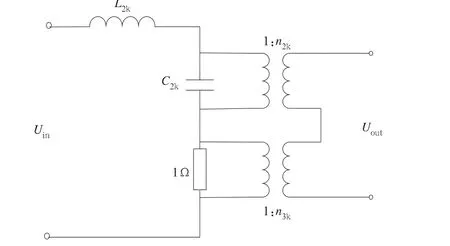
图10 h2(s)对应的电路模型
计算得到电路元件参数后,在matlab simulink中进行建模仿真。仿真电路中的变压器均为理想变压器,其变比为负数的含义为单相变压器一次侧绕组的首端与二次侧绕组的末端为同名端。

表3 降阶后的高频电路模型参数(复数极点)

表4 降阶后的高频电路模型参数(实数极点)

图11 仿真模型
3 仿真计算研究
对该牵引变压器的高压绕组分别施加二种不同类型的过电压,仿真计算其低压绕组的电压响应。
(1)施加波头时间为1.2 μs、波尾时间为50 μs、幅值为100 V的标准雷电过电压[6],低压绕组的电压响应如图12所示,响应电压局部放大图见图13所示。
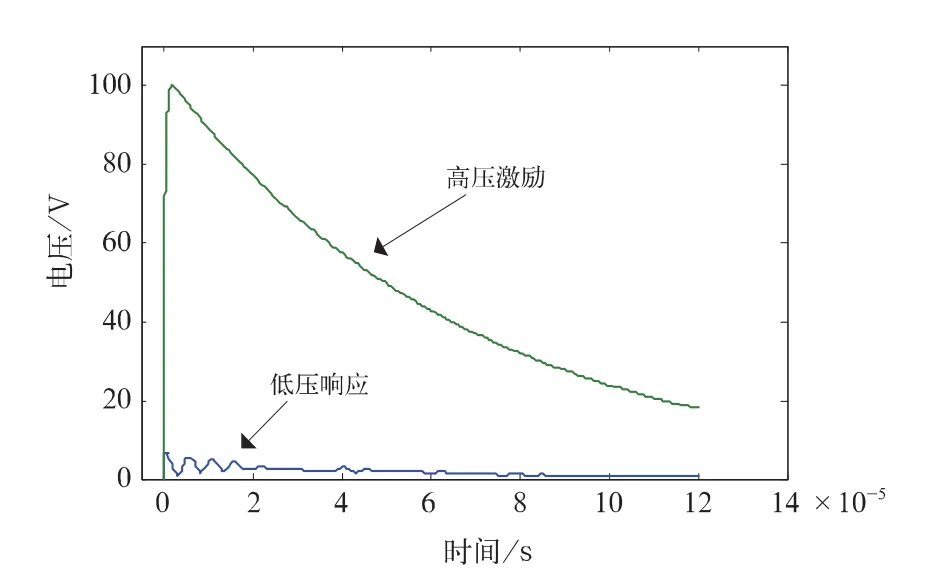
图12 标准雷电全波下的响应
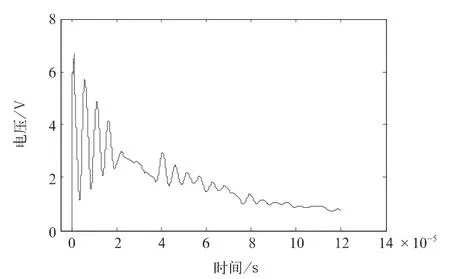
图13 响应电压放大图
(2)施加谐振频率为199.9 kHz和177.8 kHz的正弦波,其计算结果如图14和15所示。
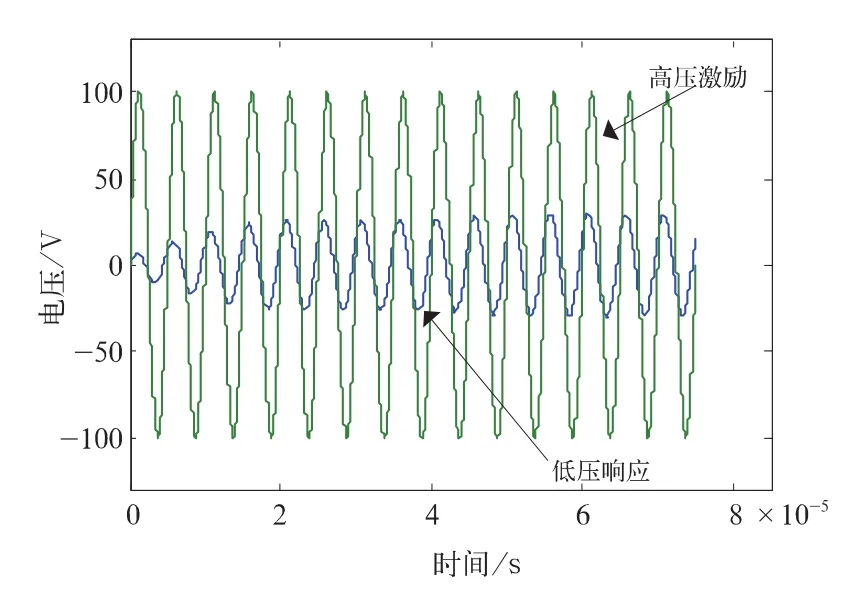
图14 199.9 kHz正弦波激励下的响应
对比两种类型激励下的响应波形可知:标准雷电冲击下的低压响应其幅值并不高,但在波头处会有高频振荡。而在谐振频率正弦波的激励下低压绕组会产生明显的谐振,并且响应电压幅值在6 μs后趋于稳定,响应电压峰值见表5所示。

图15 177.8 kHz正弦波激励下的响应
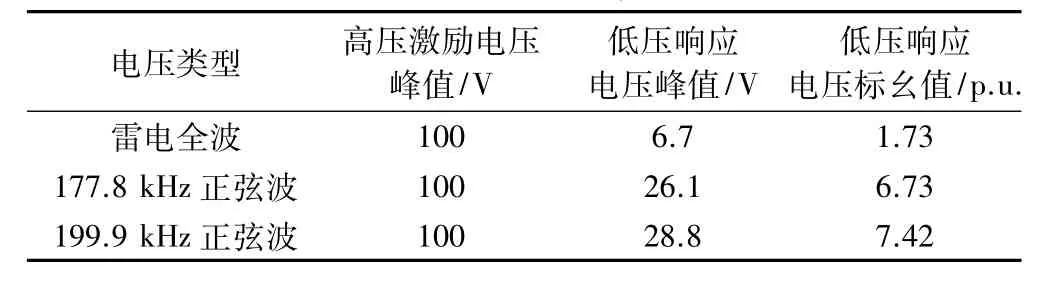
表5 响应电压峰值对比
4 结束语
通过对机车牵引变压器高、低压绕组之间传递函数的矢量匹配与降阶,运用电网络理论建立了该变压器的高频无源电路模型,并计算了二次侧绕组的过电压响应。分析表明:
该变压器的谐振频率分布范围为69~231 kHz,其中以177.83 kHz和199.98 kHz两个频率点的谐振最严重。在此谐振频率的激励下,其响应电压大约经过6 μs后会趋于稳定并达到6.73 p.u.和7.42 p.u.,这样高幅值的电压会对二次绕组的绝缘有很大影响。
另外,在标准雷电冲击下,二次侧绕组响应电压的峰值为1.73 p.u.,不会对二次绕组绝缘产生严重的危害。分析计算机车牵引变压器的谐振频率和二次绕组过电压响应,对变压器安全可靠运行以及其内部绝缘结构的设计都有重要的指导意义。
[1] 林 泓,朱仙福,盛专成.交流传动机车牵引变压器若干问题分析[J].机车电传动,1999,(4):17-20.
[2] Gustavsen B,Semlyen A.Rational Approximation of Frequency Domain Responses by Vector Fitting[J].IEEE Trans.on Power Delivery,1999,14(3):1052-1061.
[3] 梁贵书.陡波前过电压下变压器的建模及快速仿真算法研究[D].保定:华北电力大学,2007.
[4] Odabasioglu A,Celik M,Pileggi L.PRIMA:Passive Reduced-Order Interconnect Macromodeling Algorithm[J].IEEE Trans.on CAD,1998,17(8):645-653.
[5] 张喜乐,梁贵书,董华英,崔 翔,钟连宏.变压器绕组的特快速暂态建模[J].电工技术学报,2007,22(3):55-59.
[6] 刘铁英.分段层式干式变压器线圈波过程及传输特性研究[D].哈尔滨:哈尔滨理工大学,2009.
Calculation of Transient Overvoltage in Secondary Winding of Electrical Locomotive Traction Transformer
HE Jian
(CSR Zhuzhou Electric Motor Co.,Ltd.,Zhuzhou 412001 Hunan,China)
In order to research the voltage response in secondary winding of electrical locomotive traction transformer suffering from the transient overvoltage,transfer function is used to compute the resonant frequencies and voltage response in secondary winding of electrical locomotive traction transformer.Firstly,the transfer function between primary and secondary winding is measured,then this voltage transfer function is fitted with rational functions by vector fitting and order-reduced by Arnoldi algorithm.The resonant frequencies are achieved based on the transfer function.Then the order-reduced transfer function is synthesized to a circuit model which is only composed of passive elements R,L,C and ideal transformers.The voltage response of secondary winding is easily shaped by inputting the different excitations into this circuit model.
electrical locomotive traction transformer;transfer function;high frequency circuit model;transient overvoltage
U264.3+6
A
10.3969/j.issn.1008-7842.2015.01.07
1008-7842(2015)01-0036-05
)男,工程师(
2014-07-03)

