局部寻优算子库在复合材料层合板强度优化设计中的应用

沈阳航空航天大学辽宁省飞行器复合材料结构分析与仿真重点实验室 王共冬

沈阳航空航天大学航空航天工程学部 陈 浩 王 军

复合材料凭借强度高、刚度大、质量轻，并且抗疲劳、减振、耐高温等一系列优点在航空航天领域得到广泛应用[1]，复合材料层合板的优化设计变得尤为重要。大量的研究工作集中在层合板优化算法上，例如模拟退火算法、遗传算法、响应面法、分支界定理论、粒子群算法、人工蚁群算法等。Fzlzon、Faggiani[2]使用遗传算法改进了复合材料层合板的二次不稳定性的屈服强度，研究了二次不稳定性对结构设计的影响；Carrera、Miglioretti[3]根据经典复合材料层合板理论，用遗传算法对不同边界条件、力学特性的薄板的剪切变形的高阶理论和多层板理论进行了优化研究；Marín、Trias[4]利用神经网络和遗传算法对复合材料层合板在湿热载荷下的刚度进行了优化；Sadr、Ghashochi[5]以层合板的层数、铺层角度、边界条件和层合板的长宽比为设计条件，用精英遗传算法和有限条法对复合材料层合板的基本频率进行了优化设计；Jin[6]利用主从式并行遗传算法对大型翼盒类零件的结构进行了优化，使优化时间更短，效率更高；Seresta等[7]提出了一个简单的适用于多层叠复合材料层合板设计的遗传算法框架，有效地解决了独立设计层合板时相邻层合板间不匹配的问题。李真等[8]利用改进后的蚁群算法对复合材料层合板的最小层数和铺层角度进行了优化，证明了改进后的蚁群算法效率更高，速度更快；谢强等[9]构建了求解三维应力的准三维有限元模型，进行了基于渐进损伤的复合材料层合板的强度预测；李明等[10]分析了含孔的复合材料层合板的破坏模式和拉伸强度，研究了孔的形状和位置对层合板强度的影响。

目前基本遗传算法在实际的工程优化中存在着大量不足，如搜索效率低、易“早熟”，不能保持个体的多样性等。针对遗传算法的这些不足，本文对遗传算法进行改进，加入了局部寻优策略，建立了局部寻优算子库，采用强度比建立适应度函数，对复合材料层合板的强度进行了优化。详细分析了局部寻优算子库中的贪婪算法和模拟退火算法，并将2种算法进行比较，研究分析了局部寻优算子对遗传算法和最优铺层顺序的影响。

1 优化设计模型

1.1 适应度函数的确定

针对复合材料层合板结构的优化设计，以强度为优化目标，并引入强度比的概念。强度比就是层合板在作用应力下，极限应力的某个分量与其对应的作用应力分量的比：

其中/是层合板的许用应力，也是层合板的复杂应力的分量；=为工作载荷在层压壳结构件上引起的工作应力分量。将许用应力=/代入Hill-蔡（S. W. Tsai）强度理论，可以推导出关于强度比R的二次方程：

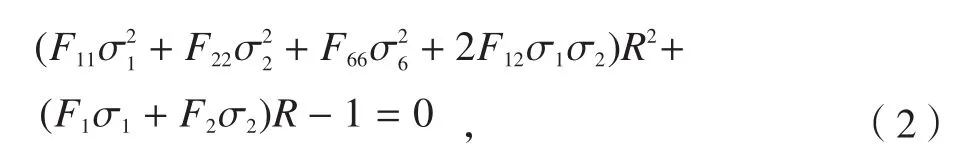
式中，σ6=τ12，而强度系数张量F ij、F i可以用材料的拉伸/压缩/剪切强度确定：

由式（1）的定义可知，R可以表示材料的安全系数，R=2时意味着工作应力还得增大1倍材料才能失效；于是材料失效时，还可增加的应力倍数为R-1，本文中的优化模型的适应度函数可表示为[11]：

其中，n为层合板的层数，(R(i)为每单层的强度比。本文中的优化过程可以做如下表述：给定载荷和层合板的厚度及层数，先确定每个层合板中单层板强度比的最小值，然后再比较这些最小值，找到最小值中的最大值，就是要求的层合板。比如A（i i=1，2，3，…，k）为层合板，a k（j j=1，2，3，…，n）为第k个层合板的单层板，首先确定a k（j j=1，2，3，…，n）的最小值akl（取l时为强度比最小值），然后找出每个层合板的ail，再从这些强度比最小值ail中找出最大值am l，这样就找出了最优化的层合板A m。

1.2 层合板优化的约束条件

在铺层结构设计中，有很多的设计要求，而本设计模型遵守以下约束条件：避免使用同一方向的铺层组（连续铺层为铺层组），如果使用，不得多于4层。

1.3 染色体的编码策略及解码

本优化模型选用的铺层顺序为0°、±45°、90°标准铺层4个铺层角度，是离散型的铺层角度，所以本文中的染色体编码策略采用实数编码。本算法中的染色体编码策略和解码过程为：

编码：[0°，45°，-45°，90°] →[1，2，3，4]；

解码：[1，2，3，4] →[0°，45°，-45°，90°] 。

1.4 遗传操作

（1）选择。本文中的选择算子采用的是比例选择算子。个体被选择的概率与其适应度成正比[12]，设种群大小为M，个体i的适应度函数为fi，则个体i被选中的概率pi为：

（2）交叉。本文的选择的交叉方式为单点交叉。所谓单点交叉就是指在个体编码中随机产生一个交叉点，然后两个相配对染色体在交换交叉点前面的染色体。

（3）变异。本文中的变异方式为：在基因串中随机选择一个变异位置，然后从基因串中的[1、2、3、4]随机产生一个实数替换该位上的数值（基因值）。

2 算法的描述

改进后的遗传算法和基本遗传算法的根本区别就在于在遗传操作之后加入了局部寻优算子，大量的局部寻优算子建立了局部寻优算子库，图1是本文算法的流程图。

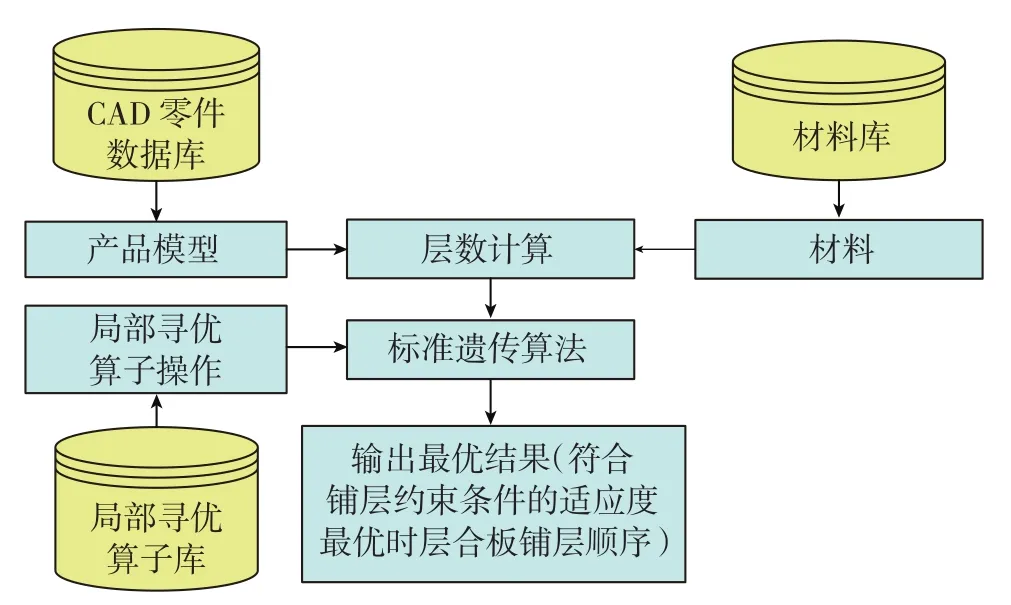
图1 基于局部寻优算子库的遗传算法流程图Fig.1 Genetic algorithm flowchart based on local optimization operator library

本文开发的优化系统可以通过局部寻优算子库中算子的选择，构成不同的遗传算法，可以通过不同的算法得到不同的优化结果，从而使优化结果更具多样性和实用性。其算子库的构成形式见表1。

本文主要对其中模拟退火算子和贪心算子进行研究。

3 数值算例

3.1 数值算例的给出

假定有1个100mm×100mm对称均衡复合材料层合板需要设计,优化目标是拉伸强度最大，层合板由16层单层组成，每单层板的厚度h0=0.125mm，载荷Mx=My=Mxy=0，Nx=500kN/mm，Nxy=Ny=0。本算例中选用的材料的力学性能见表2。算例中的局部寻优算子从算子库中选取，为了说明改进后的遗传算法的先进性，本文分别选用了模拟退火算法和贪恋算法对其进行优化计算，基本参数见表3。

表1 局部寻优算子库的结构

3.2 计算过程及其结果

图2是利用面向对象编程工具开发层合板强度的优化系统。在图2界面中左边是材料的选定和算法参数的设置以及施加载荷的大小，界面的中间部分是程序运行的适应度值进化图和局部寻优算子库，而界面的最右边的显示框内显示的是迭代进化的过程（包括进化的遗传代数以及当前代数的的适应度值和对应的解）。

由图2可知在不考虑层间应力的情况下，单一材料的层合板仅在X向受载的时候，要求拉伸强度最大的理想铺层结果是[08]s，优化结果较直观和容易理解。但实际生产中为了减少2种定向层之间的层间分层，应使每一单层组中单层尽量少，一般不超过4层。这样出现了理论优化结果和实际应用不相符情况，所以本文加入了一个铺层约束（防分层约束）。图3是2种改进算法与标准遗传算法得到的结果比较。

3.3 优化结果分析

（1）由图2可以看出，不给任何优化约束时的标准遗传算法经过强度优化后的最优适应度对应的铺层度数全部为0°，这样是不符合复合材料层合板的工程应用的，必须对优化结果进行约束调整。按照本文设定的优化约束条件对其进行约束，得到的铺层结果由原来的0°层组变成了[0/0/-45/0/0/45/0/0]s铺层顺序，符合复合材料层合板的工程应用，使本文中的算法对层合板的优化更具实用性。

表2 材料的力学性能

表3 改进后遗传算法参数

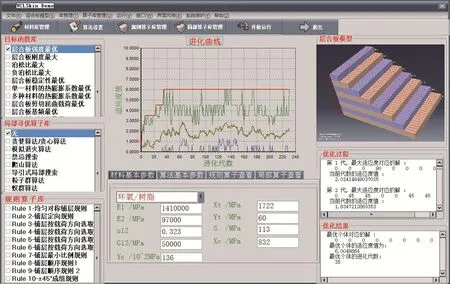
图2 层合板铺层优化界面Fig.2 Main menu of optimization of laminate

（2）由图3（a）分析可以得出，标准遗传算法中的适应度函数收敛到4.04743082，达到最优解，需要在第47代才能实现；而加入了模拟退火局部寻优的改进后的遗传算法在第13代就得到了适应度函数最大值4.04743082，得到最优解。收敛速度上加以比较的话，基于模拟退火的改进后的遗传算法要优于标准的遗传算法，更适合复合材料层合板的铺层顺序优化。同样分析图3（b）也可以得出同样的结论。

（3）由图3（b）分析可以得出，改进后的遗传算法在优化过程中的第7代进入早熟，但在第16代跳出早熟，优化到最优解；而标准遗传算法则分别在在第4到第24代进入早熟，到第25代才优化到最优。这说明改进后的遗传算法比标准遗传算法能更快更好地跳出早熟，更快地收敛到最优解。同样分析图3（a）也可以得出同样的结论。

4 结论

以复合材料层合板拉伸强度比为优化对象，利用改进后的遗传算法进行建模，借助面向对象编程语言，开发了复合材料层合板强度优化系统，建立了局部搜索算子库。该系统可以选定材料属性，设定好改进后的遗传算法的参数，以及选择局部搜索算子，计算出相对应的铺层顺序。

在铺层优化过程中引入了铺层优化的约束条件，很好地利用实际生产中的经验条件，提高了优化结果的实用性；在算法设计时，引入了局部寻优算子库，可以选择不同的改进后的遗传算法对铺层顺序进行优化，提高了优化结果的准确性。

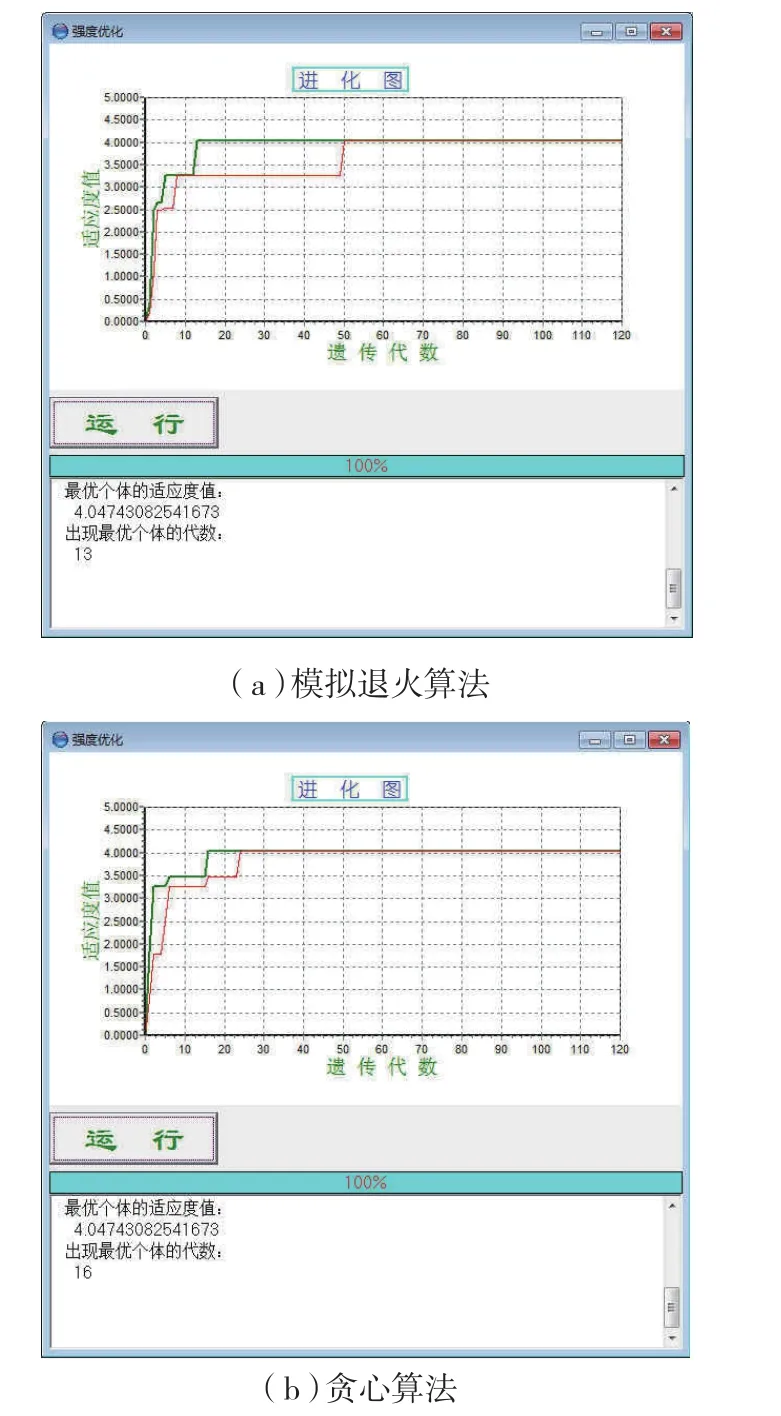
图3 改进GA和SGA运行结果的比较Fig.3 Operation result comparison between improved genetic algorithms and standard genetic algorithm

[1] 张大厚，王继辉.复合材料在建筑领域的使用现状及发展方向.武汉理工大学学报，2009，31(4):63-66.

[2] Falzon B G， Faggiani A. The use of a genetic algorithm to improve the post buckling strength of stiffened composite panels susceptible to secondary instabilities. Composite Structures， 2012，94(3):883-895.

[3] Carrera E，Miglioretti F. Selection of appropriate multilayered plate theories by using a genetic like algorithm. Composite Structures，2012， 94(3):1175-1186.

[4] Marín L，Trias D， Badalló P，et al. Optimization of composite stiffened panels under mechanical and hygrothermal loads using neural networks and genetic algorithms. Composite Structures，2012， 94(11):3321-3326.

[5] Sadr M H， Ghashochi B H. Optimization of laminated composite plates for maximum fundamental frequency using Elitist-Genetic algorithm and finite strip method. Journal of Global Optimization，2012， 54(4):707-728.

[6] Jin P. Structure optimization of large composite wing box with parallel genetic algorithm. Journal of Aircraft， 2011，48(6):2145-2148.

[7] Seresta O， Abdalla M M. A genetic algorithm based blending scheme for design of multiple composite laminates//Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures， Structural Dynamics and Materials Conference. Washington: American Institute of Aeronautics and Astronautics， 2009:318-329

[8] 李真，陈秀华，汪海. 基于蚁群算法的复合材料层合板屈曲优化.上海交通大学学报，2012，46(5)：768-773.

[9] 谢强，李亚智，李彪等. 基于准三维有限元模型的复合材料层合板强度预测.科学技术与工程，2012，12(13)：3160-3165.

[10] 李明，马力，吴林志，等. 含孔复合材料层合板拉伸强度研究.哈尔滨工业大学学报，2011(S1):1-5.

[11] 王共冬，陈彦海，邱福生. 基于启发式知识和自适用遗传算法的复合材料铺层优化设计.玻璃钢/复合材料，2009(2)：3-6.

[12] 冯消冰，黄海，王伟，等. 基于遗传算法的层压板强度优化设计.玻璃钢/复合材料，2012(3)：7-13.