基于线性方程模型的经济赔偿方案的建立

姜妍　刘羽　金晗　张铭升　沈玉波

摘 要：文章结合2014年“深圳杯”数学建模夏令营C题，运用线性方程模型，建立了经济补偿与污染物之间的线性关系。

关键词：线性方程；经济补偿；模型

1 概述

文章结合2014年“深圳杯”数学建模夏令营C题垃圾焚烧厂的经济补偿问题，运用线性方程对经济补偿方案进行求解，其用层次分析法求得的权重作为影响系数，建立了经济补偿与各污染物浓度的线性方程。

2 污染物浓度分析

（1）根據我国环境空气质量标准（GB3095-2012），空气污染物浓度限值如表1（注：文章中一、二级浓度限值取平均值）。

（2）由上述4、5中模型求得的各污染物在不同地点的浓度和（1）中表1可知，在距离垃圾焚烧厂100m距离之外的污染物浓度远小于空气污染物浓度限值（文章中一、二级浓度限值取平均值），但是考虑到时间累积、气候、风向、空气湿度等因素的影响，我们在不同地点动态监测的污染物浓度基础上，乘以一个系数n，作为标准，乘以系数之后，如果污染物浓度大于空气污染物限定浓度，则根据各污染物浓度进行居民风险经济补偿；反之，如果污染物浓度小于空气污染物限定浓度，则不赔偿。

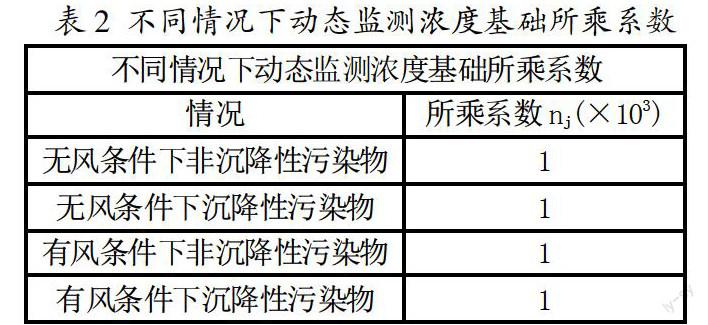
（3）不同情况下（静风条件下非沉降性污染物、静风条件下沉降性污染物，有风条件下非沉降性污染物、有风条件下沉降性污染物）动态监测浓度基础所乘系数n如表2。

3 线性方程建立与求解

3.1 模型假设

（1）假设居民风险承担经济赔偿与各污染物浓度呈线性关系；

（2）假设距离污染源每100m进行一个测点，进行经济赔偿；

（3）假设各污染物之间相互独立。

3.2 相关符号（表3）

3.3 模型建立

则得到居民风险承担经济赔偿与各污染物浓度的线性方程为：

S=？撞i=1kihj（Ci-Di）mi+P 若Ci

3.4 模型求解

我们选取一个算例（有风条件下距离污染源1000m处经济赔偿金额）进行求解。

已知距离污染源1000m处HCL、SO2、NOX、颗粒物、汞、铅、二噁英浓度分别为：0.160？滋g/m3、0.256？滋g/m3、0.801？滋g/m3、0.0672？滋g/m3、3.28×10-4？滋g/m3；3.28×10-3？滋g/m3；3.24×10-4？滋g/m3由层次分析法得到的HCL、SO2、NOX、颗粒物、汞、铅、二噁英系数ki分别为：0.1512、0.1660、0.1647、0.1849、0.1048、0.1013、0.1270。

参考文献

[1]郑阿奇，等.MATLAB实用教程[M].北京：电子工业出版社，2005.

[2]李学文，李炳照，王宏洲.数学建模优秀论文（2005-2010）[M].北京：清华大学出版社，2011.

[3]周凯，宋军全，邬学军.数学建模竞赛入门与提高[M].浙江：浙江大学出版社，2012.