用最小区域法求直线度误差的探讨

摘 要：最小区域算法是通过对最小宽度或者直径包容区的测量，以保证测量的实际相互值要能够对理想数据进行变动，按照这样的思路，去寻找最为理想要素的直线。文章就将对最小区域算法求直线误差进行研究。

关键词：最小区域法；直线度误差；最小条件

1 基本原理及处理

直线度是一个基本的几何要素，用于表示零件的形状，目前有很多方法都可以对平面内的直线度进行测量，并且可以很好的保证测量精度和稳定性，同时也有很多方法可以用于评定，比较常见的是两端点连线法、最小二乘法以及最小区域法，各自有优缺点以及适应的情况，在使用中要灵活选用。

2 两端点连线

两端点连线法首先要将首位两个采样点进行连接，然后以这个连线作为基线来对直线度的误差进行评定，先算出△h也就是各个采样点的偏差值距离首尾两点连线的长度，然后再计算出我们测量对象所拥有的直线度误差值f，具体如图1所示，详细的解答步骤如下：（1）基线的方程我们可以根据首尾两点得出，为：y=ax+b；（2）△hi=（yi-axi-b）/。根据上面的公式可以计算出各个采样点Pi距离基线之间的长度，并且将采样点和基线之间距离的最大值hmax和最小值hmin一并算出。（3）直线度的误差最后根据下面的采样点分布情况计算得出：a.当测量数据的位置分布在评定基线左右两侧的时候，我们可以得出直线度误差f为：f=hmax+hmin。b.当测量数据的位置分布在评定基线的上方位置那一侧的时候，直线度误差f为：f=hmax。c.当测量数据分布的位置在评定基线的下方位置那一侧的时候，我们可以计算出直线误差f的值为：f=hmin。

3 最小二乘法

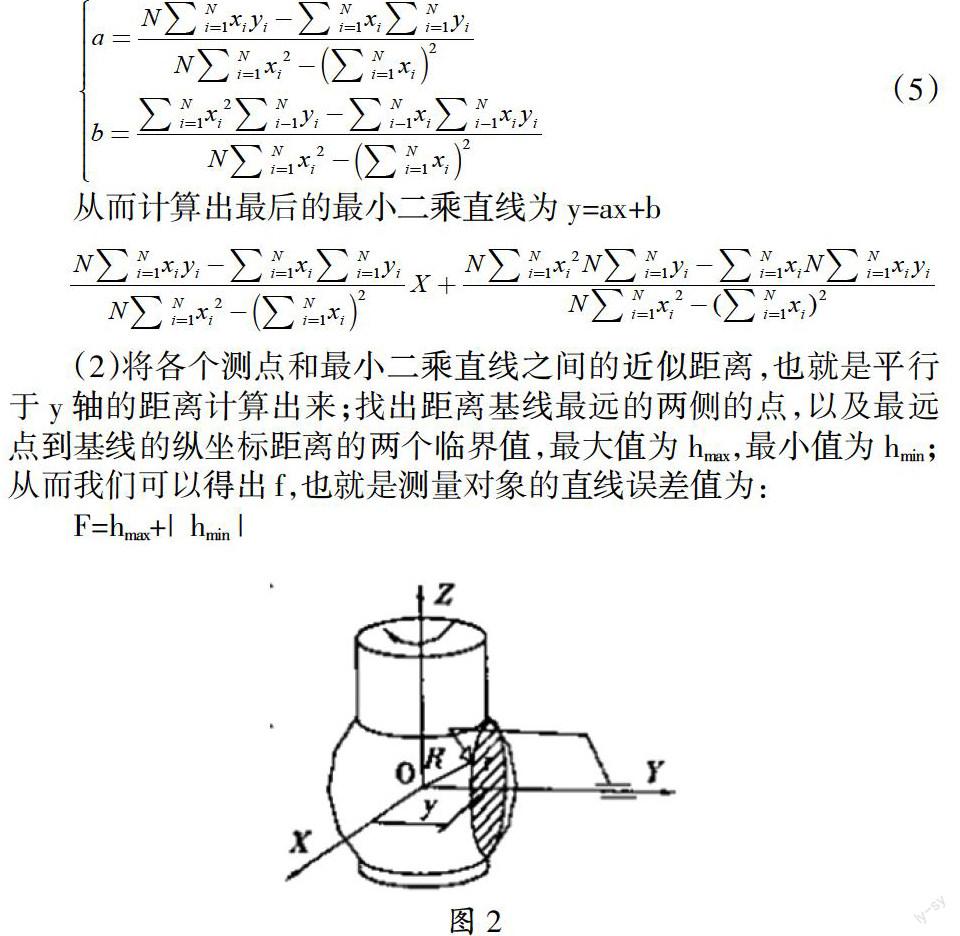
最小二乘法中的评定基线是各个采样点偏差值的最小二乘直线，首先找出和评定基线两侧距离最远的点，然后计算出这个最远点到基线的纵坐标距离himax和himin，最后将平面内的直线度误差值计算出来。

4 最小区域法

最小区域法是指将包容被测线的两两平行的直线找出来，然后在这许多对两两平行的直线中找出彼此之间距离最近的一对包容线，然后计算出直线度的误差。图3为最小区域法求出直线度误差的示意图。

最小区域法在表达形式方面不能采用解析的形式，目前来说近似用最小区域法解出直线度误差的方法中比较常见的是旋转法，也就是将y=ax+b这个一元线性方程中的斜率a进行改变，从而进行搜索逼近，例如逐次逼近旋转法；而构造包容线法和分割逼近法等都是比较常见的求解直线误差度的最小区域法，优点是准确度非常高。接下来主要对构造包容线法进行一下简单的说明：

（1）通过上文中提到的最小二乘法将采样点的最小二乘拟合直线计算出来；（2）将最小二乘直线看作是基线，基线上方的一侧我们称为高点，而基线下方的一侧称为低点；然后将各个测点区都分为高、低两点；（3）任意选择两高点或者两低点，然后将其连接形成直线，如果这条直线的上下两侧均没有采样点，那么就可以将其看作是上包容线或者下包容线；然后将距离这条直线最远的采样点作与基线平行的另一条包容线，然后将两条包容线之间的距离计算出来；最后将所有在包容条件范围内的两高点与对应低点、两低點和对应高点之间形成的平行线的距离ti；（4）找出距离中的最小值tmin，则这个数值就是直线度误差值中符合最小条件的。

5 结束语

两端点连线法最小二乘法和最小区域法是比较常见的三种直线度评定方法，其中精度最低的是两端点连线法，精度最高并且误差最小的是最小区域法，并且得出的结论是唯一的。但是最小区域法来计算直线度的误差时难度较大，计算复杂，所以一般用于精度要求较高的情况，通常来说使用最多的还是最小二乘法。

参考文献

[1]张新宝，张坤.平面内直线度误差最小区域法的完备性研究[J].机械工程学报，2012，24：14-18.

[2]阚萍，贺晓春.评定直线度误差数据处理方法的分析与比较[J].工具技术，2014，10：86-89.

[3]林家春，石照耀.基于力学基础的最小区域直线度误差凸包求解方法[J].北京工业大学学报，2010，12：1585-1589.

[4]辛帅，李研.改进的蜂群算法评定空间直线度误差[J].电子设计工程，2011，13：64-66.

作者简介：左倩（1989-），女，汉族，陕西省延安市人，工学硕士，单位：西安工业大学机电工程学院，研究方向：精密测量。