基于汽车租赁调度的最优化问题研究
余剑秋 周蔚 许冬梅
[摘 要]文章针对汽车租赁调度的最优化问题,通过构建基于线性规划的最低转运费模型,使用Lingo等软件进行编程,得出在满足需求量为前提下最优汽车租赁调度方案,并给出相关分析与评价。
[关键词]汽车租赁;线性规划;Lingo[DOI]10-13939/j-cnki-zgsc-2015-27-097
1 引 言
汽车租赁行业早在70余年前就已经在美国迅速发展,时至今日,已经培养出赫兹、安飞土等行业巨头。其中赫兹旗下用于汽车租赁业务的汽车已达150万辆以上,在全球拥有数千个网点,分布在150多个国家。
在中国,汽车租赁行业发展已经近二十年。早期的汽车租赁行业主要是面向外企、大型国企等企业用户。真正大规模投入个人业务的也是近几年的事情。随着中国汽车产业和中国社会经济的迅猛发展,人们的消费水平和出行需求也相应提升。这为汽车租赁行业的规模化发展创造了优越的条件。而随着汽车租赁行业的发展,如何进行汽车的调度最优化问题被提上日程。
某城市有一家汽车租赁公司,此公司年初在全市范围内有379辆可供租赁的汽车,分布于20个代理点中。根据所给出的相关问题与实际情况相结合,对汽车租赁公司汽车调度最优化问题进行研究。
二十个代理点分布
2 分析思路
根据已知的未来四周各代理点的汽车需求量,设计最优调运方案使运费最低。应建立线性规划模型,以转运费最低为目标函数,求调运方案的最优解。通过初步计算发现,未来四周每天的汽车需求总量各不相同,有时需求会大于供给,此时应设置虚拟供给地,并依据差额确定虚拟供给地的供给量;当供给大于需求时,应设置虚拟需求地,根据供求差额确定需求量。
3 基于线性规划的最低转运费模型
3-1 模型的准备
①对于给定各代理点坐标,对其欧式距离进行求解:
假设第i个代理点与第j个代理点的坐标分别为(xi, yi)(xj, yj),那么
dij=1-2[KF(](xi-xj)2+(yi-yj)2[KF)]
②对一辆车从第i个代理点调运到第j个代理点的总运费cij求解:
cij=1-2[KF(](xi-xj)2+(yi-yj)2[KF)]mij
③对于②中,当i=j时,即同一代理点向自身调运,显然cij=0。
3-2 模型的建立
设xij表示代理点i(供应地)向代理点j(需求地)调运的汽车数量,其中i=1, 2, 3, …, 20; j=1, 2, 3, …, 20。
为了尽量满足需求,即使得Eik=Dik
minZ=[DD(]20[]i=1[DD)][DD(]20[]j=1[DD)]xijkcij
s-t[JB({][DD(]20[]j=1[DD)]xijk=Eik i=1, 2, 3, …, 20k=1, 2, 3, …, 28
[DD(]20[]i=1[DD)]xijk=Dik i=1, 2, 3, …, 20k=1, 2, 3, …, 28
xijk≥0 i=1, 2, 3, …, 20k=1, 2, 3, …, 28[JB)]
其中: Eik——调运前第i个代理点第k日拥有的车辆数;
Dik——未来四周内第i个代理点第k日的汽车需求量;
xijk——第k日第i个代理点向第j个代理点转运的车辆;
cij——从第i个代理点向第j个代理点调运需要的总费用。
4 最优汽车租赁调度方案
4-1 最小转运费
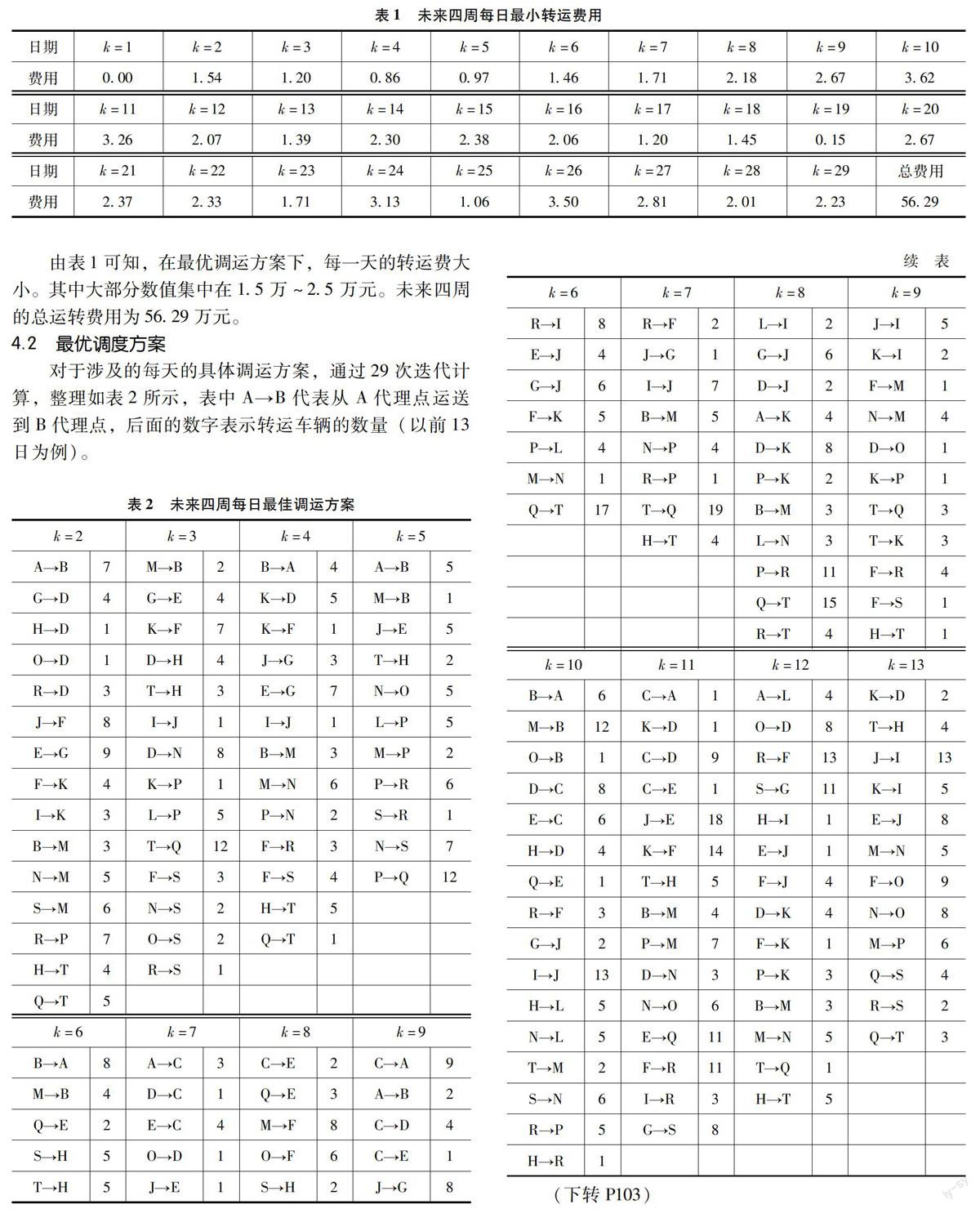
根据模型对未来四周内每天调度费最低的方案进行求解,依据第一天的调运方案结果,作为第2天各调运点初始车辆,以此类推,依次进行29天的迭代计算。编写LINGO程序,计算结果如下表,其中由于第1日的需求量和供给量刚好相等,所以不需要调运。
表1 未来四周每日最小转运费用
在29天的方案中,我们发现第19日需要调转的车辆最少,涉及的代理点也最少。第9、10、14、18日调运涉及的代理点最多,车辆也较多。以第29天为例,调运方案为从M点调运到B点8辆汽车,从G点调运到D点12辆汽车,从K点调运到D点3辆汽车,从G点调运到J点15辆汽车,从E点调运到J点4辆汽车,从I点调运到L点1辆汽车,从N点调运到L点1辆汽车,从E点调运到M点5辆汽车,从F点调运到M点9辆汽车,从N点调运到M点1辆汽车,从S点调运到M点8辆汽车,从H点调运到O点3辆汽车,从S点调运到O点1辆汽车,从R点调运到P点7辆汽车,从E点调运到Q点4辆汽车,从T点调运到R点2辆汽车。总的调运费为2-23万元。
参考文献:
[1]安徽财经大学-2014年安徽财经大学暑期数学建模模拟题[EB/OL].[2014-09-23].http://zhujm1973-blog-163-comblogstatic/ 315513552014923288768/.
[2]张家善-线性规划在产销不平衡运输问题中的应用[J].中国市场,2010(19):19-20.
[3]杨文忠-运筹优化在物资不平衡调运中的应用研究[J].物流技术,2013(15):150-153-
[4]叶桂林-Lingo软件在运输优化问题中的应用[J].现代商业,2011(23):13.
[5]金晶晶-Lingo软件在数学建模竞赛中的应用[J].十堰职业技术学院学报,2010(4):85-88-