排序算法在某系统中的应用

曹小阳　王琨

摘 要：排序是计算机程序设计中的一种重要操作，它的功能是将一个数据元素或记录的任意序列，重新排列成一个按中轴点有序的序列。本文简要论述几种常见的排序算法，重点讨论快速排序及其优化。

关键词：中轴点；快速排序；分治；优化

一、前言

某系统软件在整个运行过程中采集和分析终端数据，并以列表形式终端信息。为方便查看，需要根据信息类型进行排序。因此，学习和研究各种排序算法是系统软件开发人员的重要课题之一。

二、排序算法简介

由于待排序的记录数量不同，使得排序过程中涉及的存储器不同，可将排序方法分为内部排序和外部排序两大类。内部排序指的是待排序记录存放在计算机随机存储器中进行的排序过程；外部排序指的是待排序记录的数量很大，以致内存一次不能容纳全部记录，在排序过程中尚需对外存进行访问的排序过程。本文只讨论内部排序。内部排序的方法很多，但就其全面性能而言，很难提出一种被认为是最好的方法，每一种方法都有各自的优缺点，适合在不同的环境下使用。按排序过程中依据的不同原则对内部排序方法进行分类，大致可分为插入排序、交换排序、选择排序、归并排序和基数排序。

插入排序将一个数据插入到已经排好序的有序序列中，从而得到一个新的、个数加一的有序序列；交换排序根据序列中两个记录键值的比较结果来对换这两个记录在序列中的位置，将键值较大的记录向序列的尾部移动，键值较小的记录向序列的前部移动；选择排序每一趟在记录中选取中轴点最小的记录作为有序序列中第i个记录；归并排序将两个已经排序的序列合并成一个序列；基数排序借助多中轴点排序的思想对单逻辑中轴点进行排序。

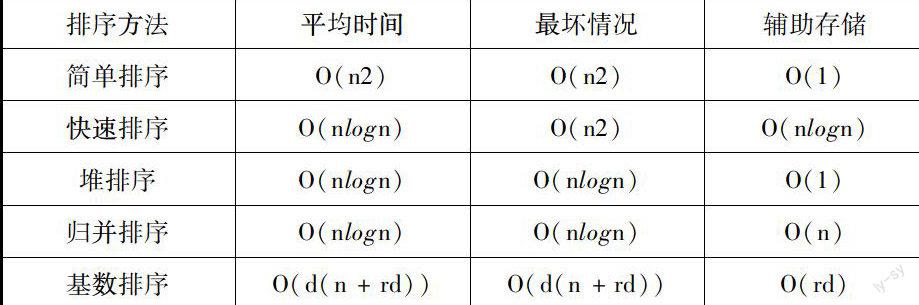
各内部排序方法的平均时间、最坏情况和所需辅助存储如下：

从平均时间性能而言，快速排序最佳，其所需时间最省。

三、快速排序算法及优化

软件采用快速排序算法。快速排序是由冒泡排序改进而得的，它的基本思想是：在待排序的n个记录中任取一个记录（通常取第一个记录），把该记录放在最终的位置后，数据序列被此记录分割成两部分。所有中轴点比该记录中轴点小的放置在前一部分，所有比它大的放置在后一部分，并把该记录排在这两部分的中间，这个过程称作一趟快速排序。之后对所有的两部分分别重复上述过程，直至每部分内只有一个记录为止。

一趟快速排序采用从两头向中间扫描的方法，同时交换与基准记录逆序的记录。

假设T（n）为n个记录r[1，n]进行排序所需时间，则由算法可得：

T（n）=Tpass（n）+T（k-1）+T（n-k）

其中Tpass（n）为对n个记录进行一趟快速排序所需时间，由算法可知，它和记录数n成正比，可以cn表示；T（k-1）和T（n-k）分别为对r[1，k-1]和r[k+1，n]中记录进行快速排序所需时间。如果待排序列中的记录是随机排列的，则在一趟排序之后，k取1至n之间任何一值的概率相同，快速排序所需时间的平均值则为knlnn。

在所有同数量级的排序方法中，快速排序的常数因子k最小。因此，就平均时间而言，快速排序是目前被认为是最好的一种内部排序方法。但是，若初始记录序列按中轴点有序或基本有序时，快速排序将马上退化到起泡排序，其时间复杂度为O（n2），这是由于选定的中轴点每次都会跟剩余的所有元素做比较，每一次的排序只能使待排序列减一。显然，该情况下，排序算法的效率很低。究其原因，是算法每次都选择左端点作为中轴点。

由上面可知影响快速排序速度的一个重要因素是中轴点的选取，可以将中轴点的选择随机化，不再是固定选择左端点，而是利用随机数生成一个有效的位置作为中轴点。在有序序列的排序上面，改进后的算法有很大进步，但是当待排序列中所有元素相等时，仍然会出现最坏情况，时间复杂度为O（n2）。

理想情况下，选择中轴点时，最佳选择是将待排序列划分为两个相等长度的子序列，但是要达到这种状态需要经过大量计算，会带来时间消耗，一种近似的估计取法是随机选择三个排序元素并且用三个元素的中值作为中轴点。

针对包含大量重复元素的序列，理想情况下是在一次排序完成后，下一次排序不需要再对重复元素进行比较，即相同元素不参与后续的递归，改进方法是在一次排序后，将与中轴点相同的元素放在一起，减少迭代次数，将待排序列划分为三个区域：小于中轴点，等于中轴点，大于中轴点。

算法步骤如下：

1、将与中轴点相同的元素放到序列兩端；

2、一次排序结束后将两端相同元素放到中轴点周围。

软件采用该算法对终端信息进行排序，效率得到明显提升。

四、结束语

系统的正常运行，表明该排序算法可满足现有需求。但是，算法还存在缺陷，当待排序列足够小时，插入排序的效率很高，可以将算法改进为在排序前判断待排序列大小，当待排序列元素个数小于某一个值时使用插入排序。（作者单位：南京模拟技术研究所）

参考文献：

[1] 严蔚敏，吴伟民.数据结构.清华大学出版社，2007-04.

[2] 李春葆.数据结构.清华大学出版社，2004-01.

[3] Stanley B.Lippman、Josee Lajoie.C++Primer第三版，潘爱民、张丽译.中国电力出版社，2002-05.

[4] Mark Allen Weiss.数据结构与算法分析，冯舜玺译.机械工业出版社，2004-01.

[5] 程杰.大话数据结构.清华大学出版社，2011-06.

[6] Thomas H.Cormen、Charles E.leiserson、Ronald L.Rivest et al.算法导论，殷建平、徐云、王刚译.机械工业出版社，2013-01.

[7] Anany Levitin.算法设计与分析基础，潘彦译.清华大学出版社，2014-1.

[8] Sedgewick.算法，谢路云译.人民邮电出版社，2012-10.