特征多项式的倒量即为m序列的推导

【摘要】 本文主要结合矩阵论知识分析了m序列与其特征多项式之间的关系，并利用matlab进行仿真实验，将长除特征多项式与仿真输出序列得到的序列进行比对。

【关键词】 特征多项式 m序列 MATLAB

m序列是一种最长的线性移位寄存器序列，同时也是一种非常重要的伪随机序列，这种序列有比较好的自相关特性而且易于产生。m序列在直扩系统中用来对要传递的信号进行扩展，m序列在跳频系统中主要用于控制跳频系统的频率合成器，并生成随机跳频图案[1]。更重要的是m序列可由它的特征多项式直接计算产生出来，本文将对它的计算式进行推导，并给出基于matlab的软件仿真结果。

此外，本文的涉及到的运算都是模二运算，运算结果最终都是除2取余，即xmod2，例如：2mod2=0，7mod2=1等等。

一、问题描述

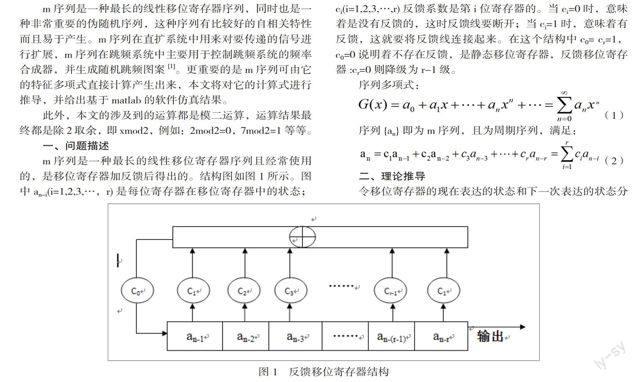
m序列是一种最长的线性移位寄存器序列且经常使用的，是移位寄存器加反馈后得出的。结构图如图1所示。图中an-i（i=1，2，3，…，r）是每位寄存器在移位寄存器中的状态；ci（i=1，2，3，…，r）反馈系数是第i位寄存器的。当ci=0时，意味着是没有反馈的，这时反馈线要断开；当ci=1时，意味着有反馈，这就要将反馈线连接起来。在这个结构中c0= cr=1，c0=0说明着不存在反馈，是静态移位寄存器，反馈移位寄存器：cr=0则降级为r-1级。

序列多项式：

（1）

序列{an}即为m序列，且为周期序列，满足：

（2）

二、理论推导

令移位寄存器的现在表达的状态和下一次表达的状态分别由矢量bn和bn+1表示，分别为：

bn=[an-1 an-2 an-3 … an-r]T （3）

bn+1=[a（n+1）-1 a（n+1）-2 a（n+1）-3 … a（n+1）-r]T （4）

取状态转移矩阵A为：

（5）

则将有：

（6）

那么m时刻的状态与现态之间的关系为：

（7）

当Ammod2=E且m=2r-1时，m序列为该反馈移位寄存器产生的序列。

下面求A的特征多项式：

（8）

由此可得：

（9）

即

（10）

经整理后

（11）

由Caley-Hamilton定理：一个满足自己的特征方程rxr矩阵，即

（12）

根据A的特征方程，我们定义特征多项式f（x）为：

（13）

接下来推导G（x）与f（x）之间的关系：

令线性移位寄存器序列为：

{an}=a0，a1，a2，…，an，…

相应的序列多项式为：

（14）

{an}的线性递归反馈函数为

（15）

则

（16）

交换求和次序并做变量代换：

（17）

整理后，并考虑c0=1，则有

（18）

选择移位寄存器的最初状态为a-r，a-r+1=…=a-2=a-1=0，则式（17）的分子

（19）

由此可得：

（20）

三、实验数据和结果

3.1给定m序列性质的验证

特征多项式为，m=2r-1=25-1=31，其状态转移矩阵为：

（21）

1、周期性

运行matlab，输入A^31得：

（22）

对A^31进行模二运算rem（A^31，2）得：

（23）

2、最长序列性

下面抽取计算A的11，13，23，29，30次幂，验证其最长性：计算结果如下：

3.2 m序列的产生

仍以特征多项式为f（x）=1+x2+x5的m序列为例。

1、长除法求

由理论推导结果G（x）=1/ f（x）对f（x）进行长除得：

（24）

2、Matlab反馈仿真移位寄存器

取移位寄存器起始值為pninitial=[0 0 0 0 1]，由特征多项式能得反馈系数为：

（25）

状态矩阵为：

（26）

产生的m序列如图2：

由图2可以看出m序列的周期为31，即：

（27）

五、结果分析与说明

从以上实验，我们可以得出以下结论：

1）多项式长除法和matlab仿真反馈移位寄存器得出的结果完全一致，这充分说明了序列多项式与特征多项式之间存在倒量关系；

2）m序列特征矩阵的周期性由A^31mod2=E验证；

3）周期恰好为2r-1时，A的其它次幂均不等于E充分说明了序列的最长性。

参 考 文 献

[1]李新，何传江.矩阵理论及其应用.重庆：重庆大学出版社，2005

[2]曾兴雯，刘乃安，孙献璞.扩展频谱通信及其多址技术.西安：西安电子科技大学出版社，2004

[3]赵鸿图，茅艳，赵军良等，通信原理MATLAB仿真教程，北京：人民邮电出版社，2010

[4]陈海龙，李宏.基于MATLAB 的伪随机序列的产生和分析[J].计算机仿真.2005

作者简介：房万顺（1991.05）男，天津人，就读于山西师范大学，所学专业：电子信息工程。