二叉排序树平均查找长度的精确表达式

程希明 王昕

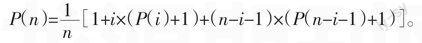
[摘 要]查找长度的精确表达式，需要对二叉排序树的平均查找长度进行详细分析，寻找一个平均查找长度的精确表达式及其证明过程。基于二叉树表，提出欧拉常数的一种新的计算方法，对平均查找长度精确表达式进行了算例分析，并与其他经典平均查找长度计算公式加以对比，验证了其正确性。

[关键词]二叉排序树 平均查找长度 欧拉常数

[中图分类号] TP311.12[文献标识码] A[文章编号] 2095-3437（2015）07-0100-02

《数据结构》作为一门介于数学、计算机硬件和计算机软件三者之间的核心课程，是信息与计算科学相关专业的综合性专业基础必修课。树形结构是该课程的重要内容之一，掌握二叉树的逻辑结构特性、各种存储结构的特点及适用范围，有助于学生学会对处理的数据建立抽象数据类型，并使学生对算法的复杂度有一定的分析能力。

在数据处理中，查找是一种经常使用的操作方法，树表中数据元素的插入和删除均需要进行查找操作。查找是指在含有若干记录的表中找出关键字值与给定值相同的记录。若表中存在这样的记录，则查找成功，返回所找到记录的信息或记录在表中的位置;否则查找失败，返回空记录或空指针。当用线性表作为表的组织形式时，可以有三种查找法，其中二分查找效率最高。但由于二分查找要求表中结点按关键字有序，且不能用链表作存储结构，因此，当表的插入或删除操作频繁时，为维护表的有序性，势必要移动表中很多结点。这种由移动结点引起的额外时间开销，就会抵消二分查找的优点。也就是说，二分查找只适用于静态查找表，若要对动态查找表进行高效率的查找，可采用二叉排序树作为表的组织形式。

二叉排序树，作为树形结构的一个重要类型，又称二叉查找树，亦称二叉搜索树，其存储结构和算法比较简单，特别适合计算机处理。它或者是一棵空树，或者是具有下列性质的二叉树[1]：（1）它的左子树上的所有结点（若存在）的值均小于根结点的值;（2）它的右子树上的所有结点（若存在）的值均不小于根结点的值;（3）它的左、右子树也分别为二叉排序树。

例如，由一组关键字（18，5，20，9，6，27，3）可构造如图1所示的二叉排序树。

二叉排序树是一种动态树表，树的结构通常不是一次生成的，而是在查找过程中，当树中不存在关键字等于给定值的结点时再进行插入。新插入的结点一定是一个新添加的叶子结点，并且是查找不成功时，查找路径上访问的最后一个结点的左孩子或右孩子结点。

崔尚森等[2]提出了基于表地址前缀分布特点的前缀长度二分查找方案;秦玉平等[3]给出了常用查找算法平均查找长度的计算方法，包括查找成功和查找失败平均查找长度的计算。本文给出了一个关于二叉树平均查找长度的精确表达式及其证明过程，并给出了算例验证。

一、二叉树的平均查找长度

查找运算的主要操作是进行关键字的比较，为确定给定关键字在查找表中的位置，需和给定关键字进行比较，将比较次数的期望值称为平均查找长度。

假设任意给定n个记录，每个记录带有可比较大小的关键字，将这n个记录排成一棵二叉排序树，假定在查找成功的情况下，要求出这棵二叉排序树的平均查找长度。

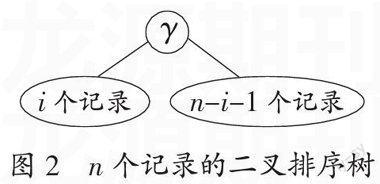
不妨设这n个记录中有i个记录的关键字比第一个记录的关键字小，有n-i-1个记录的关键字不比第一个记录的关键字小，如图2所示。

由此得到的二叉排序树在每个记录等概率被查的情况下，其平均查找长度为：

其中P（k）表示含k个结点的二叉排序树的平均查找长度。由于这n个记录是任意的，所以它们的排列次序具有随机性。

即下列事件：

Ai=“i个记录的关键字比第一个记录的关键字小，n-i-1个记录的关键字比第一个记录的关键字小”（i=0，1，2，…，n-1）是等概率出现的。

所以有：

显然P（0）=0，P（1）=1，当n？叟2时，严蔚敏、吴伟民[4]给出了（1）式的一个估计上限：

P（n）？燮1+4logn。                                       （2）

二、平均查找长度的精确表达式

下面，我们给出（1）式的精确表达式。

引理：如果n？叟2，n？叟k？叟1，则

定理：（1）式中P（n）的表达式是

证明：在（1）式中计算P（n）·n2-P（n-1）·（n-1）2的递推式。

对（5）式做下列一系列变形：

上列各式连同（5）式左右分别相加，整理得：

利用引理且整理得：

考虑到P（1）=1，所以           ，从而证明了（4）。

当n较大时，（4）式有一个近似式：

P（n）=2lnn+2C-3。                                    （6）

其中C是Eular常数，0.577215？燮C？燮0.577216。

三、算例验证

我们可以简单地验证一下定理的正确性。当n=3时，三个记录的排列情况有六种，即γ1<γ2<γ3，γ1<γ3<γ2，γ2<γ1<γ3，γ3<γ1<γ2，γ2<γ3<γ1，γ3<γ2<γ1，六种情况分别对应图3所示六种排序树：

图3（a）、3（b）、3（e）、3（f）所示的四种情况下，排序树的平均查找长度都是×（1+2+3）=2;图3（c）和3（d）两种情况的平均查找长度为×（1+2+2）=。以上六种情况出现的概率均等。所以对三个结点的查找表来说，P（3）=×（2×4+×2）=。这与公式（4）式计算的结果完全吻合。

[ 参 考 文 献 ]

[1] Mark Allen Weiss.数据结构与算法分析[M].北京：机械工业出版社，2004.

[2] 崔尚森，冯博琴，张白一.一种前缀长度二分查找的改进算法[J].计算机工程，2007（15）：70-72.

[3] 秦玉平，王丽君，刘伟.查找算法平均查找长度的计算方法[J].渤海大学学报（自然科学版），2011（4）：354-357.

[4] 严蔚敏，吴伟民.数据结构[M].北京：清华大学出版社，1992.

[责任编辑：钟伟芳]