重型汽车制动压力提升后对后桥推力杆受力的影响

张守伟 景振龙 唐锐 魏海巍

摘 要：本文通过计算对重型汽车制动压力提升后对后桥推力杆受力的影响进行了简要分析，为整车制动系统压力提升提供了理论依据。

关键词：重型汽车制动系统；后桥推力杆；后桥制动力

1 概述

目前，欧洲重型汽车气制动系统的行车制动气压普遍采用10bar，而我国的行车制动气压普遍采用8.5bar。提升行车制动气压，可以增大制动力，缩短制动距离，提高行车安全。但由于制动系统压力的提高，车辆制动时的减速度会如何变化，是否会对整车的悬架系统带来影响，例如双后桥车型后桥推力杆的受力，在增大制动系统压力后，车辆制动时减速度变化较多的话，可能会超出推力杆的受力极限，甚至产生致命的破坏效果。本文通过计算确定不同气压下的制动减速度的变化情况，并通过整车试验分析推力杆受力，以此验证提高系统压力的可行性。

2 制动减速度的计算

2.1 整车模型参数：

整车模型以6x4双后桥牵引汽车为例，其主要参数如下：

满载整车质量 32000kg

满载前轴静载荷 6000kg

满载中后桥静载荷 26000kg

满载质心高度 hg=1.3m

满载质心距前桥中心 A=3.17m

满载质心距中后桥中心 B=0.73m

车轮静力半径 rk=0.5625m

地面附着系数 φ0=0.8

2.2 系统初始压力为10bar时，满载工况下最大减速度计算：

初始气压为10Bar，第一次制动时的气压按P1=9Bar计算，根据

Ff1=

前桥制动力是：Ff1=80995N

同理后桥制动力是：Ff2=168420N

制动力分配系数：β==0.32474

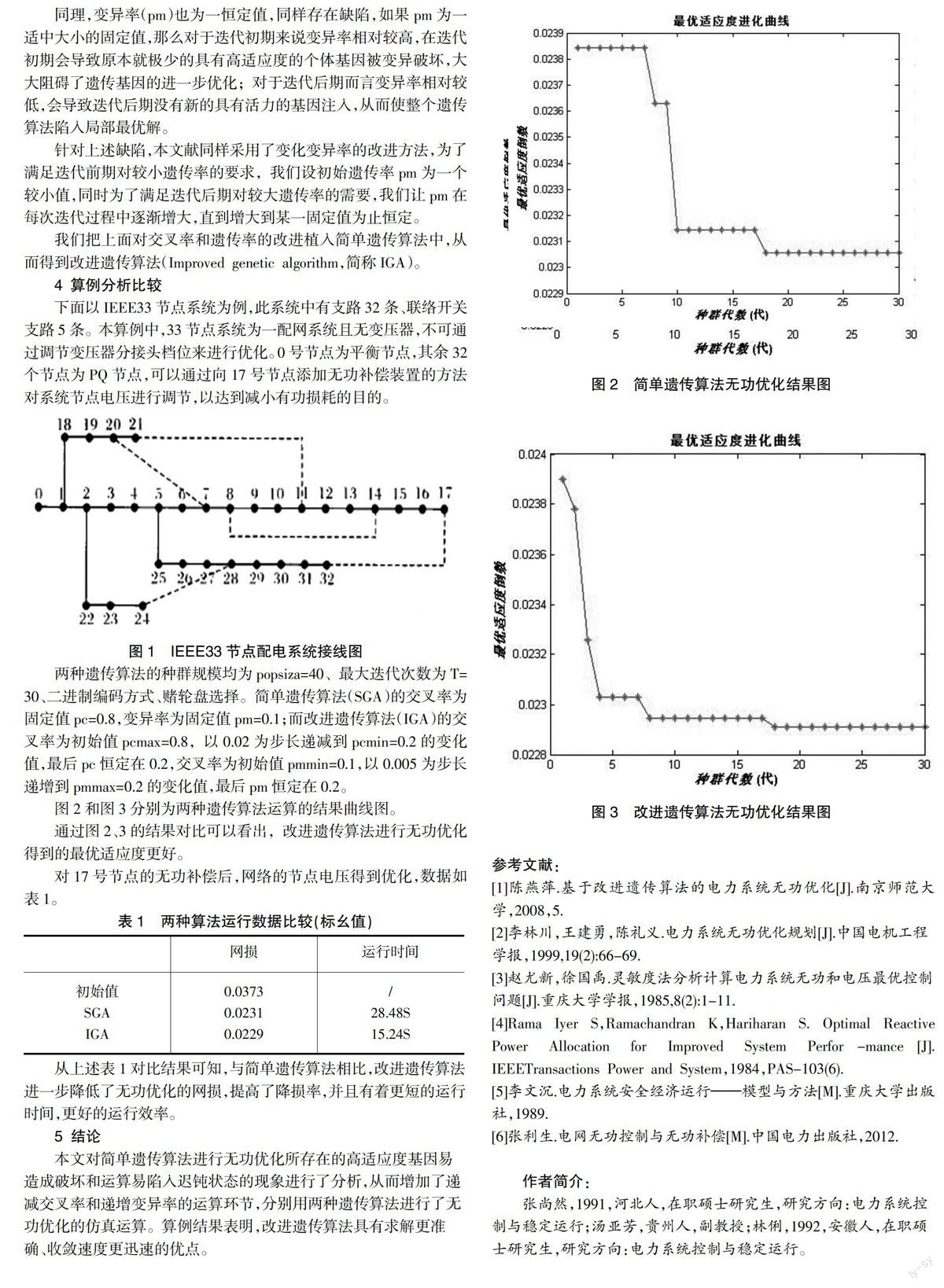
根据制动力分配系数可以绘制出满载车辆I曲线、β线、f线组和r线组，见图1：

通过曲线分析，在前轴制动力为80995N及之前，β线和φ=0.8r线有交点A，β线和φ=0.8f线没有交点，故前轴不会抱死，而后桥会在A点抱死；如图1所示，点A即为后桥抱死点。

制动时，前桥的制动力为：Ff1=8099N（1）

后桥的制动力则取地面提供的最大制动力

FB2=（L1-q×hg）φ（2）

又有，Ff1+FB2=Gq

把式（1）、（2）带入（3）可以求出：q=0.717

车辆减速度：a=qg=0.717×9.8=7.03m/s2

2.3 系统初始压力为8.5bar时，满载工况下最大减速度计算：

初始气压为8.5bar，第一次制动时的气压按P1=7.5 bar计算，此处计算过程与2.2相同，同理可得：q=0.65

车辆减速度：a=qg=0.65×9.8=6.37m/s2

2.4 小结

由此我们可以看出，车辆制动系统压力由8.5bar提升至10bar后，整车满载制动时的最大减速度由6.37m/s2增大为7.03m/s2。而空载工况下由于制动时前后桥均会抱死，其制动减速度不变，在此不再详细计算。因此，下一步我们需要验证制动减速度增大后，对后桥推力杆受力的影响。

3 后桥推力杆受力的变化

后桥推力杆在悬架系统中的作用是防止中后桥的移位，如車辆制动或加速时防止桥前、后移位，其受力的变化直接影响悬架的可靠性。因此，当我们提升制动压力，导致车辆的制动减速度变化时，推力杆的受力必然发生变化。下面，我们通过不同工况下的制动试验来对后桥推力杆的受力进行分析。

试验中一共安装了四个传感器，用于测量推力杆横截面每平方毫米的受力大小，它们分别位于中桥上推力杆（A点）、中桥下推力杆（B点）、后桥上推力杆（C点）、后桥下推力杆（D点）。试验又分为满载和空载两种状态。故在8.5bar和10bar两种压力下，做对比试验时，就形成了8组对比数据：A点空载、A点满载、B点空载、B点满载、C点空载、C点满载、D点空载、D点满载。下面就每组数据进行对比分析：

如上数据，在8组对比数据中，有两组不增反降，它们是A点满载和B点空载；有四组数据略有增加，增加幅度在4%以内：A点空载、B点满载、D点空载、D点满载；而在C点位置，增幅有所增大，C点满载增加了17.7%，C点空载增加了6.7%。但是，从应力的数值上来看，在C点，不管是空载还是满载，都要比B点和D点要小，特别是满载状态下，要小很多。

下面对数据的局部进行分析，从所有的数据上看，出现了两个大于50 的数据，他们分别是：满载状态下系统压力为8.5时，ABS失效53N/mm2，前轴失效50N/mm2。可见系统压力提升后，推力杆的受力更加均衡，压力提升前受力大的推力杆受力有所减小，而压力提升前受力小的推力杆受力较大增加。

因此，我们可以得出制动系统压力由8.5bar提升到10bar后，对推力杆的影响很小，可以满足要求。

4 结束语

本文所介绍的整车制动减速度的计算和后桥推力杆受力变化的验证分析方法，为整车制动系统压力提升提供了理论和试验依据。

参考文献：

[1]余志生，等.汽车理论[M].机械工业出版社，2006.

[2]刘地，等.商用车辆和挂车制动系统技术要求和试验方法[S].中国标准出版社，2014.

[3]尹福炎.金属箔式应变片制作工艺原理[M].国防工业出版社，

2011.