三电平变流器高电压穿越下的中点电压控制研究
孙健++刘刚++赵宇++高亚春++牛虎++宋堃


摘 要: 针对高电压穿越条件,分析中点钳位型三电平变流器的中点电压数学模型,推导出三相功率与零序电压的传递函数。提出一种新型的注入零序电压控制方案,该方案通过控制中点处的零序总功率为0,来实现中点电压的平衡控制。具体方案是,通过计算中点处的三相功率偏差,经PI调节器输出零序电压调制波,经过3s/2s坐标变换,叠加至三相基波调制波,并采用SVPWM调制算法实现。仿真显示,该方案能够实现中点电压的平衡控制,具有较好的动态响应。
关键词: 三电平变流器; 中点钳位; 中点电压平衡; 零序电压
中图分类号: TN911?34; TM761 文献标识码: A 文章编号: 1004?373X(2015)10?0151?05
0 引 言
目前,国内风电装机容量居于世界第一,但产生了产能过剩、发电质量低、电网不稳定等现象。对国内的大型集中式风电场,当风场负载突变、SVC等无功补偿装置的投入时,容易引起电网过压,并导致风电机组的跳闸脱网。针对高电压穿越技术(HVRT),国外已有完整的标准,如澳大利亚AEM、加拿大AESO、爱尔兰EIRGRID、丹麦Energinet.dk。它们在低电压穿越、高电压穿越等方面都有详细的标准规范和技术要求[1]。国内并没有关于HVRT的国家统一标准,如《GBT_19963?2011风电场接入电力系统技术规定》只有低电压穿越(LVRT)的相关标准,没有HVRT的具体标准。国内的冀北电科院提出了一些HVRT标准,并在2013年1月,针对金风科技做了首次的HVRT测试工作,但只限于地方使用,不能成为行业标准。
对NPC三电平变流器,HVRT过程中,中点电压的偏移比正常运行波动更加剧烈,控制难度也更大。针对中点电压平衡控制,文献集中在两种方向:一是改进硬件方案,改变中点电压、电流的特性;二是改进软件算法,对中点电压进行控制[2?3]。其中,软件方案常见的有滞环控制、零序分量注入法。
文献[4]针对不同的零序分量注入法做了详细研究,对控制环路的设计总结出3种方案。但其局限性在于,对控制环路传递函数的选取不当,导致传递函数存在符号性,即系统开环传递函数与流入电容电流的方向有关,给控制器的设计带来了困难。
本文在文献[4]的基础上,重新选取控制环路的传递函数,设计出可变参数的PI调节器,并验证在HVRT条件下,比文献先[4]的方案具有更好的控制效果。
本文的具体方案是,选取注入中点处的三相功率平衡(即总功率为0)作为控制目标,推导出中点处三相功率、交流侧零序电压调制波之间的传递函数,通过设计PI控制器得到交流侧零序电压调制波。本文选取的传递函数没有了符号方向,对系统的稳定性控制更为容易,能够实现HVRT恶劣工况下的中点电压平衡控制。
1 NPC三电平变流器的原理
1.1 NPC三电平变流器的数学模型
NPC三电平PWM变流器在a,b,c静止坐标系下的数学模型为:
[Ldiadt=usa-iaR-ucaLdibdt=usb-ibR-ucbLdicdt=usc-icR-ucc] (1)
式中:[L、R]为等效阻抗;[us]为电网侧电压;[uc]为三电平变流器交流侧电压。
图1 三电平PWM变流器的等效电路图
1.2 三电平变流器的控制策略
考虑到HVRT状态下,电网电压会出现不平衡波动,本文采用d?q正负序解耦控制方案生成调制波,并采用最近三矢量SVPWM调制算法生成PWM脉冲,见图2。
图2 d?q正负序解耦原理图
根据式(2)可得到的实现基波正负序分离的d?q分量:
[u*d+=ud+-ud-cos2ωt-uq-sin2ωtu*q+=ud++ud-sin2ωt-uq-cos2ωtu*d-=ud--ud+cos2ωt+ud+sin2ωtu*q-=ud--ud+sin2ωt-ud+cos2ωt] (2)
式中:LPF滤波器为[F(s)]:[F(s)=1Tss+1],[Ts=1δω0];[ω0]为电压基频;[δ]为常数,本文取[δ=0.707]。
下面简介正序d?q分量的控制方案:
对式(1)进行正负序解耦变换,可得变流器在正序d?q坐标系下的数学模型:
[Ldiddt=-Rid+ωLiq+usd-udLdiqdt=-Riq-ωLid+usq-uq] (3)
式中:[ud,uq]为变流器交流侧电压的d?q轴分量;[usd,usq]为电网电压的d?q轴分量。
将同步旋转坐标系的d轴定向于电网电压矢量[us]的方向上,则d轴表示有功分量参考轴,而q轴表示无功分量参考轴[5]。
将式(3)改写为:
[ud=-(Ldiddt+Rid)+ωLiq+usd =-ud′+Δud+usduq=-(Ldiqdt+Riq)-ωLid+usq =-uq′+Δuq+usq] (4)
式中:
[ud′=Ldiddt+Riduq′=Ldiqdt+Riq, Δud=ωLiqΔuq=-ωLid] (5)
式中:[ud′],[uq′]与各自的电流分量具有一阶微分关系,可用电流闭环PI调节器计算得到;[Δud],[Δuq]为消除定子电压、电流交叉耦合的补偿项;电网电压[usd],[usq]作为前馈补偿。
2 中点电压的控制方案
2.1 中点电压的数学模型
下面分析中点电压的数学模型[6?7]。
设参考电压矢量[Vref=Vejθ],则参考矢量电压的三相瞬时值[usa,usb,usc]为:
[usausbusc= Vcosθusacos(θ-23π)usacos(θ+23π)] (6)
设负载功率因素角为[φ],则电流矢量为[Iref=Iej(θ-φ)],三相电流[ia,ib,ic]的瞬时值表达式为:
[iaibic= Icos(θ-φ)Icos(θ-φ-23π)Icos(θ-φ+23π)] (7)
中点电压即上下电容的电压偏差:
[Δudc=udc1-udc2] (8)
从中点处分析,三相电路注入中点处的零序功率[ΔSa,ΔSb,ΔSc]为:
[ΔSa=ΔudciaΔSb=ΔudcibΔSc=Δudcic] (9)
另一方面,从交流侧分析,[Δua,Δub,Δuc]为交流侧的等效零序电压调制波,则[Δua,Δub,Δuc]与[Δudc]之间通过开关函数相互对应。
下面分析采用最近三矢量SVPWM调制算法时,[Δua,Δub,Δuc]与[Δudc]之间的传递函数[G(s)]。
对最近三矢量SVPWM调制[8],在6大扇区,6小扇区不相同时,开关函数也不相同,零序矢量作用时间也不同,[G(s)]实际上是非线性函数。但通过对单周期的分析,[G(s)]可以利用近似线性化方法[9?10]得到简化。
举例:第3大区第2小区,基波调制波[ua]产生电流[ia]。当在[ua]上注入[Δua]的零序电压分量时,零序电压作用时间[Ta0],其中[Δua]产生的电流增量约为[ia0]:
[Ta0=0.5Ts(1.732(ua+Δudc)/udc)sin ?ia0=Ta0ia] (10)
式中:[Ts]为调制周期,[ua]为电压矢量,[udc]为母线电压,[?]为[ua]电压的相角。于是,可得:
[G1(s)=Δua(s)ia0(s)=Ta0ia] (11)
式中:[Ta0]为非线性变量,可以缩小研究范围,只需研究每个周期[Ts]内的稳定性。考虑约束条件[Ta0<0.5Ts],故将[G1(s)]近似线性化为:
[G1(s)=Δudc(s)ia0(s)=0.5Tsia] (12)
于是可得系统的传递函数可表示为图3。
图3 系统传递函数框图
图中:[C1,C2]为电容值;[11.5Tss+1]为系统控制延时函数;[KP+KIs]为PI控制器的传递函数。于是,[ΔS]与[Δua]的传递函数为:
[G2(s)=ΔsΔua=0.5Tsi2a(C1+C2)s] (13)
2.2 基于中点功率平衡的中点电压控制方案
从图3可见,加入PI控制器之后,系统的开环传递函数为:
[Woc(s)=(KPs+KI)0.5Tsi2a(1.5Tss+1)(C1+C2)s] (14)
与文献[4]的开环传递函数:
[Woc(s)=-3imKcpcosφ(τc+1)πτc(C1+C2)s2] (15)
相比,本文的传递函数电流出现了平方项[i2a],这就保证了传递函数的符号为正,系统的稳定性更容易得到控制,控制器的设计相对简单有效。
在设计PI调节器时,将[KP,KI]参数扩大[i2a]倍,约掉[i2a]项,则可获得简单的开环传递函数:
[Woc(s)=(KP1s+KI1)0.5Ts(1.5Tss+1)(C1+C2)s] (16)
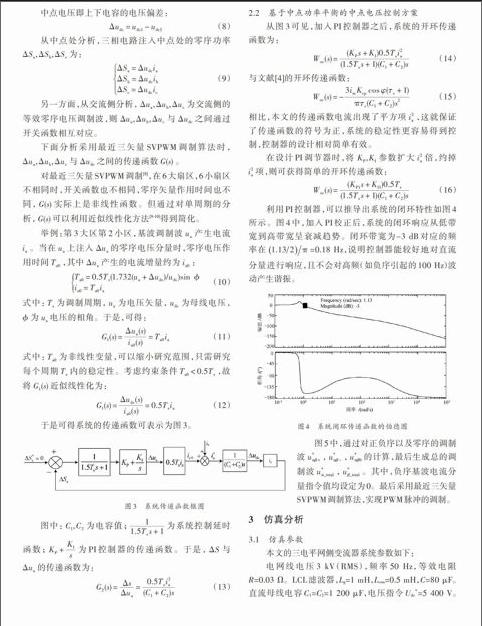
利用PI控制器,可以推导出系统的闭环特性如图4所示。图4中,加入PI校正后,系统的闭环响应从低带宽到高带宽呈衰减趋势。闭环带宽为-3 dB对应的频率在[1.132π]=0.18 Hz,说明控制器能较好地对直流分量进行响应,且不会对高频(如负序引起的100 Hz)波动产生谐振。
图4 系统闭环传递函数的伯德图
图5中,通过对正负序以及零序的调制波[u*αβ+],[u*αβ-],[u*αβ0]的计算,最后生成总的调制波[u*α_total],[u*β_total]。其中,负序基波电流分量指令值均设定为0。最后采用最近三矢量SVPWM调制算法,实现PWM脉冲的调制。
3 仿真分析
3.1 仿真参数
本文的三电平网侧变流器系统参数如下:
电网线电压3 kV(RMS),频率50 Hz,等效电阻R=0.03 Ω。LCL滤波器,Lg=1 mH,Lcon=0.5 mH,C=80 μF。直流母线电容C1=C2=1 200 μF,电压指令Udc*=5 400 V。额定电流Ie=577 A(RMS),开关频率fs=1 600 Hz。零序电压控制环的PI参数KP=5k,KI=50k。其中k=[1(i·i)],i为三相输出电流的幅值,并对k进行限幅为[0.5,10],同时对零序调制波输出限幅为[-100,100]。对HVRT的设置,1 s之前电网电压与电容均正常;1 s后Ua、Ub相电压突升至1.2 pu。以下对文献[4]的PI设计方案简称方案1,本文的方案简称方案2。
图5 中点电压控制方案框图
3.2 仿真结果
3.2.1 采用方案1的中点电压控制
图6、图7中,在t=1 s前,上下电容电压Udc1与Udc2的偏差在15 V以下。在t=1 s后,由于电网电压处于HVRT状态,方案1对中点电压的控制能力有限,Udc1与Udc2的偏差只能稳定在20~30 V之间。
图6 上下电容的电压波形
图8中,在1.5 s处对中点电压即图7进行FFT分析。分析显示,电压除了含有直流分量外,还含有50 Hz,150 Hz的分量。这是因为电压不平衡后,Udc中产生了2倍频分量,导致d轴有功分量产生100 Hz的负序分量,100 Hz分量经正序park反变换后产生50 Hz倍频的交流电压电流,经负序park反变换后产生50 Hz倍频的交流电压电流。
图7 中点电压波形
图8 对图7的FFT分析
3.2.2 采用方案2的中点电压控制
图9、图10中,在t=1 s前,上下电容电压Udc1与Udc2的偏差在15 V以下。在t=1 s后,电网电压处于HVRT状态,方案2较方案1大大改善,Udc1与Udc2的偏差能稳定在5~10 V之间,且响应速度快(小于0.5 s)。
图9 上下电容的电压波形
图10 中点电压波形
图11中,在1.5 s处对中点电压即图7进行FFT分析。分析显示,电压直流分量被较好地抑制,但由于控制器的带宽特性,无法消除50 Hz,150 Hz的分量。这是因为电压不平衡后,Udc中产生了二倍频分量,导致d轴有功分量产生100 Hz的负序分量,100 Hz分量经正序park反变换后产生50 Hz倍频的交流电压电流,经负序park反变换后产生50 Hz倍频的交流电压电流。
图11 对图10的FFT分析
4 结 语
本文针对高电压穿越的恶劣工况,对NPC三电平变流器的中点电压控制详细研究,提出了一种全新的中点电压控制方案。该方案利用近似线性化方法,推导出中点处零序功率、交流侧零序调制波之间的传递函数,设计可变参数的PI调节器,可自动调节中点电压的平衡。仿真表明,本文的方案比文献[4]的方案具有明显的稳态优势,且动态响应速度较快,可应用于新能源的高电压穿越领域,具有重要的应用价值。
参考文献
[1] 刘雪菁,朱丹,宋飞,等.风电机组高电压穿越技术研究[J].可再生能源,2013,31(11):34?38.
[2] 胡存刚,王群京,李国丽,等.基于虚拟空间矢量的三电平NPC逆变器中点电压平衡控制方法[J].电工技术学报,2009,24(5):100?107.
[3] 李宁,王跃,雷万钧,等.NPC三电平变换器中点电压控制方法综述[J].电力电子技术,2011,45(10):78?80.
[4] 姜卫东,杨柏旺,黄静,等.不同零序电压注入的NPC三电平逆变器中点电位平衡算法的比较[J].中国电机工程学报,2013,33(33):17?25.
[5] 张崇巍,张兴.PWM整流器及其控制[M].北京:机械工业出版社,2003.
[6] ALONSO O, MARROYO L, SANCHIS P, et al. Analysis of neutral?point voltage balancing problem in three?level neutral?point?clamped inverters with SVPWM modulation [C]// IEEE 2002 28th Annual Conference. [S.l.]: Industrial Electronics Society, 2002, 2: 920?925.
[7] MONGE S B,BORDONAU J,BOROYEVICH D. The nearest three virtual space vector PWM: a modulation for the comprehensive neutral?point balancing in the three?level NPC inverter [J]. IEEE Power Electronics Letters, 2004, 2(1): 11?15.
[8] YAZDANI A, IRAVANI R A. Generalized state?space averaged model of the three?level NPC converter for systematic DC?voltage?balancer and current?controller design [J]. IEEE Transactions on Power Delivery,2005, 20(2): 1105?1114.
[9] 陈新海.自适应控制及应用[M].西安:西北工业大学出版社,2003.
[10] 胡跃明.非线性控制系统理论与应用[M].北京:机械工业出版社,2005.

