一种提高干涉相位识别精度的方法

杨练根，刘丙康，王选择，2，翟中生

（1.湖北工业大学 机械工程学院，湖北 武汉430068；2.天津大学 精密测试技术及仪器国家重点实验室，天津300072）

引言

在表面形貌光学干涉测量方法中，计算干涉相位的准确性，直接决定测量结果的精度或误差。因此，在干涉相位解包裹运算之前，需要准确提取相位信息。现在应用的干涉相位提取算法主要有：三步法、四步法［1－2］、五步法［3］、FFT 算法、小波变换等［4－6］。这些算法的实质都是通过消除幅值与偏置参数的影响，获取各像素点的干涉序列的初相位。其中，三步法、四步法、五步法是研究时间较长，应用最为普遍的，它们的不同之处是抗噪声干扰能力有一定差别。传统的三步法、四步法等要求对相移驱动步长进行严格控制，因此对相移驱动要求闭环控制，增加了驱动的难度与成本。同时，测量系统对环境要求也很高，因为测量过程中微小的振动，都会导致驱动步长发生改变，对最后的测量结果影响也较大。

如何在开环相移驱动条件下，根据序列灰度图得到干涉场上各像素点的初相位信息，且保证初相位信息受环境影响小及具有较高的识别精度，是本文需要解决的核心问题。

为此，本文以四步法为基础，提出了一种不要求等步长相移驱动的高精度相位识别方法。主要思想是根据干涉场上的各像素点的灰度关联信息，在建立干涉方程组的基础上，通过椭圆拟合准确获取干涉序列相位或驱动步长。在此基础上，通过采样提取多幅干涉图的序列相位，运用Lagrange抛物插值算法，计算并构造满足相位四步法求解的相差π／2的4幅干涉灰度图［7］，经计算表明构造的干涉图的相差具有较高的精度。最后，运用四步法通过干涉灰度图得到了整个干涉场上各像素点的相位信息。

1 相移驱动步长的确定

理论上干涉图上每一像素点的序列灰度值gi可以表达为

每一像素点的交流幅值A、偏置量C与初相位θ0不同。

式中：i＝1－N，表示驱动序列点；θi为序列驱动相位，与相移驱动位移Δi满足如下关系：

由此可知，相移驱动步长与干涉相位成正比。因此，驱动步长的确定，关键在于能够准确获取干涉序列上每一点的驱动相位θi。在灰度值已知的条件下，驱动相位θi求解依赖于交流幅值A 与偏置量C的计算，下面讨论如何计算A与C。

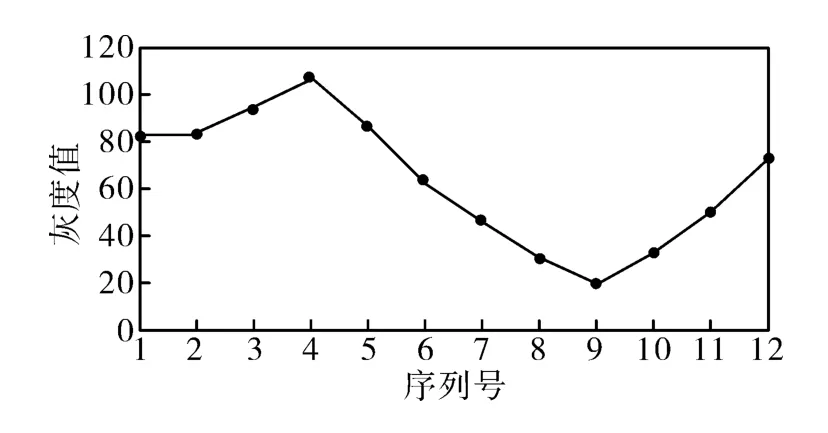
图1 单像素点的灰度序列值Fig.1 Gray value sequence of single pixel

图1为单像素点的12点灰度序列值，从图中明显可以看出，相移驱动步长不满足等步长的条件（等步长驱动时，灰度序列曲线应近似为三角函数曲线），且从满足 （1）式来看，灰度值含有较大的随机噪声。

考虑到干涉场上各点在相移驱动的任何时刻，都具有相同的驱动步长或序列驱动相位，选取干涉场上的任意两点，就可以建立如下的序列灰度值方程组：

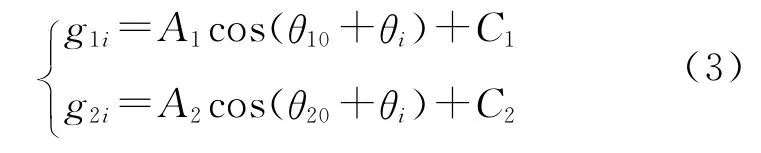
如果分别以g1i、g2i为横、纵坐标，理论上序列点所构成的轨迹为椭圆，且椭圆的中心分别为C1，C2。椭圆的参数由交流幅值A1，A2与两像素点的初相位差（θ20－θ10）决定。且当相差为π／2时，轨迹为正椭圆。通过椭圆拟合，可以得到C1，C2，A1，A2与初相位差（θ20－θ10）等5个关联参数。

1.1 提高干涉方程组的拟合精度

考虑到椭圆参数的拟合精度受像素灰度值噪声与椭圆形状的影响，所以需要恰当地选取拟合像素点，并对像素点灰度值进行降噪处理。当两像素点相差为π／2时，干涉序列灰度值满足正交关系，此时拟合椭圆具有最高的精度。因此选取参与拟合的两像素点应尽量满足相差为π／2的关系，采用的选取方案如下：

首先在某个特定区域内（一般信噪比较高的地方），对各像素点的灰度序列值进行如下的计算。

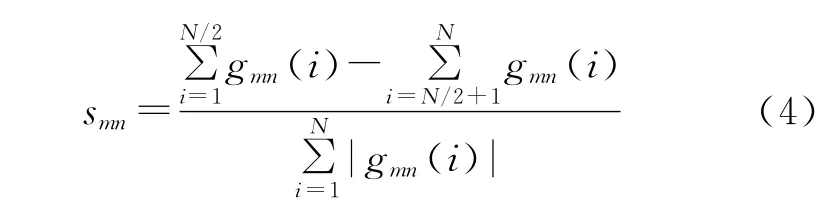
理论上，smn的大小处于［－1，1］之间。为了选取相差π／2的两点，将smn绝对值最大与最小的点作为拟合像素点。理论可以证明，当这两点的相差接近π／2时，有利于提高椭圆拟合的精度。

1.2 椭圆拟合求解

椭圆拟合主要是对椭圆直角坐标方程进行线性回归，得到回归系数，然后根据回归系数与干涉方程组参数的关系，进一步计算这些参数。

干涉方程组的椭圆直角方程可写成如下形式：

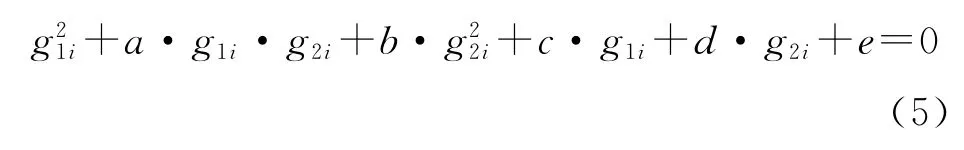
通过基于最小二乘拟合的线性回归运算后，得到系数a，b，c，d，e。

由参数方程与坐标方程的关系，可以推得：

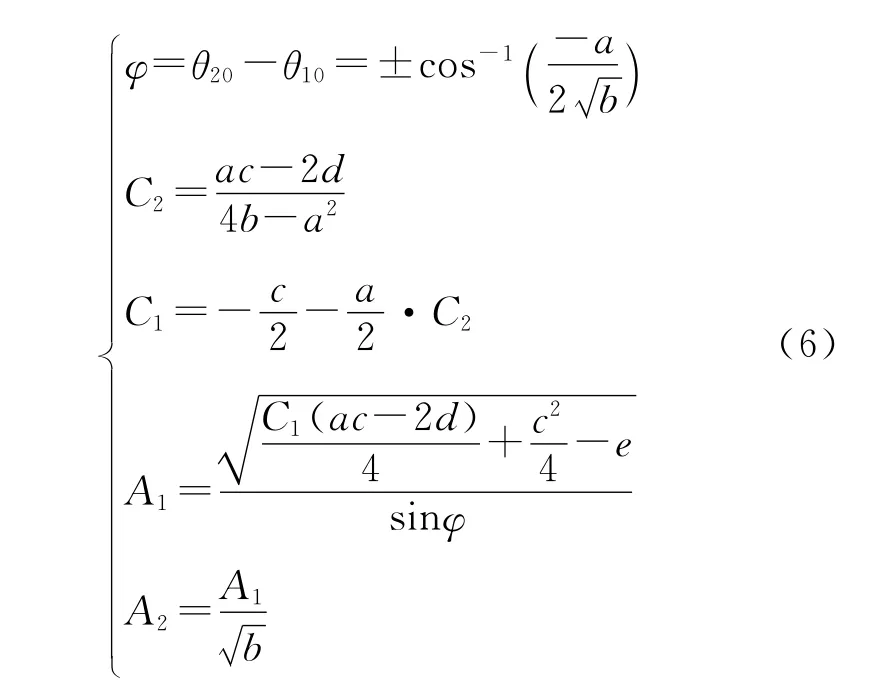
其中相位差φ的符号由灰度序列值在椭圆中的旋转方向决定。逆时针旋转时为负，顺时针旋转时为正。判断方法采用向量叉乘的方式，具体判断公式如下：若dz＞0，则取负号；反之，取正号。

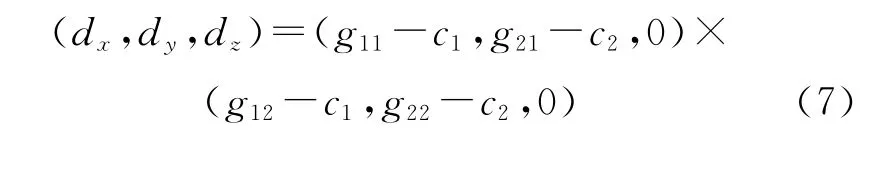
图2为降噪处理与零均化后的两像素点10个灰度序列值及其椭圆拟合结果。需要指出的是，相同条件下，对于整周期内的数据点数，其椭圆拟合精度比非整周期内数据点数拟合精度高，所以这里仅取其中的10点进行椭圆拟合。

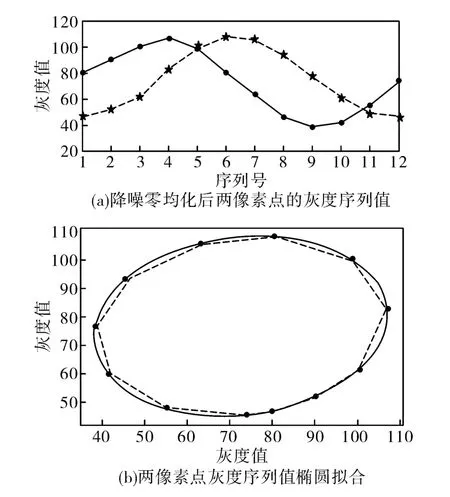
图2 灰度序列运算结果Fig.2 Calculated results of gray value sequence

1.3 计算驱动相位

根据椭圆拟合的结果，在计算得到 （6）式中的各个参数之后，在一定条件下对两灰度序列值进行相位计算。这里的条件包括：1）由于头尾两点无法确定其相位的单调性，不能计算其对应的相位，因此头尾2个点不参与计算；2）若当前点与前后两点的差分结果符号相同，就可以确定当前点相位的单调性，因此当前点与前后两灰度值差分结果gi－gi－1与gi＋1－gi同为正或同为负时，计算驱动相位，否则不予计算。

具体的计算公式如下：

式中相位符号的确定由当前点的差分符号决定，即若gi－gi－1＞0，相位符号取负，否则取正。

对灰度序列计算相位结果如表1所示：

表1 驱动相位计算结果Table 1 Results of driving phases

考虑拟合相位φ＝ －1.167 9，通过如下方法计算中间10点的驱动相位：若两序列中相应点相位都存在，则计算相位φi＝（φ1i＋φ2i－φ）／2；若仅序列1中存在，则φi＝φ1i；仅序列2中存在，φi＝φ2i－φ。并通过取2π圆整，使计算结果处在（－π，π）之间。因此，除了头尾两点相位不参与反算外，图3中虚线所代表的灰度序列在第3，7两点不参与运算；实线所代表的序列在第5，9三点不参与运算。表1中第3行为计算的驱动相位。

2 构造满足四步法的干涉灰度图

在计算出驱动相位量之后，就可以构造满足π／2相差的4幅干涉灰度图。考虑到椭圆拟合后，实际相位的计算是从采样序列的第2幅干涉图开始有效的，因此以第2幅图为起点，即以第2幅图为初相位灰度图g0，构造剩下的相差π／2的3幅干涉灰度图。

具体构造方法如下：

首先对表1中的综合相位进行解包裹运算，并通过简单运算把起点移位到零位，图3为移位前后的相位，以角度来表示。然后分别选择与π／2，π，3π／2偏差最小的3点，并计算这3个点与目标相位的偏差ε1，ε2，ε3。

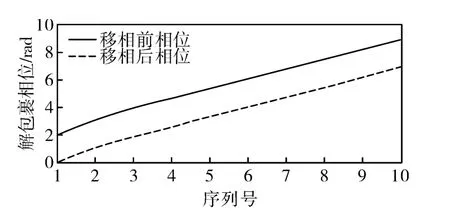
图3 驱动相位解包裹运算结果Fig.3 Unwrapping results of driving phases

例如图3中与π／2，π，3π／2偏差最小的3点分别为第3，5，7点，且以此3点为中心的弧度偏差量分别为 （－0.4145，0.3442，1.0659），（－0.5049，0.2133，0.8941），（－0.6767，0.0551，0.6656）。最后利用Lagrange抛物插值来完成目标相位灰度图像的重构，例如针对π／2的灰度值重构公式如下：

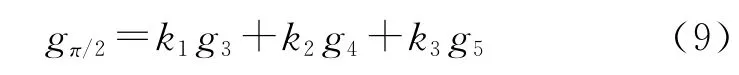
式中g2，g3，g4分别代表第2，3，4幅图像的灰度值。

重构系数k1，k2，k3分别采用如下公式计算：

使用同样的计算方法，可以得到gπ、g3π／2。通过计算Lagrange插值余项，计算结果表明：对于3幅重构图灰度值，由于Lagrange插值偏差导致的灰度值截断重构误差分别小于2.53%，1.57%，0.52%。

3 实验结果

对Ra＝0.44μm的方波多刻线粗糙度样板的表面形貌进行多波长干涉测量，该样板经中国计量科学研究院采用粗糙度国家基准校准，校准结果的不确定为U95＝5%。用上述方法对多波长干涉图的每一个波长的采样序列进行相位提取，图4为对波长550nm的干涉序列图重构的4幅相差π／2的灰度图像。传统四步法得到的4幅干涉图中包含了相移驱动和噪声干扰造成的误差，同时相移误差是四步法相位计算误差的主要来源［8］。而通过上述方法得到的4幅干涉图将相移误差转换为驱动相位计算的误差和Lagrange插值误差，这类误差可以通过增加采样次数和插值节点数目来减小。

最后利用重构灰度图进行各点相位计算。计算公式如下：

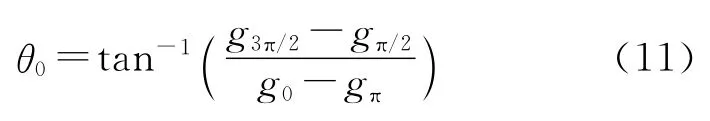
式中θ0的取值范围为（－π，π］，即通过判断分子分母的正负在4个象限内计算相位。同理，依次对波长520nm，640nm的干涉序列图进行相位提取。考虑对双波长测量［9］，当两波长差较小时，测量范围显著增大，但得到的测量结果精度很低。因此应用两近波长（520nm，550nm）的相位差在大尺度范围内识别测量结果，用两远波长（550nm，640 nm）相位差在小尺度内进一步缩小测量结果的误差，最后用单波长（550nm）相位计算最终测量结果，得到干涉图像上各点的相对高度，即被测表面的形貌信息［10－12］。最后计算粗糙度样板的Ra值为0.439 0μm，该样板测量的相对误差δ＝0.23%。

图4 重构的4幅相差π／2的干涉图像Fig.4 Reconstructing 4 interference images withπ／2 phase－difference

4 结论

该方法不要求严格的等步长驱动，简化了传统四步法对相移驱动的控制。仅通过两像素点灰度序列关联关系，把驱动步长的求解问题转化为数学上的椭圆拟合问题，并准确地获取了相移驱动相位，为高精度寻找与构造4幅干涉序列图提供了条件，对相关技术的相位识别具有指导意义。采用Lagrange抛物插值算法，使重构灰度值相对误差控制在0.5%以内。结果表明，上述方法的相对误差δ＝0.23%。因此，该方法对相移驱动要求不高，抗局部环境振动干扰能力强，受相移驱动非线性驱动误差影响小，降低了驱动与闭环控制的难度与成本，为多波长测量奠定了基础。

［1］ Song L M，Dong X X，Xi J T，et al.A new phase unwrapping algorithm based on Three wavelength phase shift profilometry method［J］.Optics ＆ Laser Technology，2013，45：319－329.

［2］ Takamasa S，Zhao X F，Osami S.Phase－locked phase－shifting laser diode interferometer with photothermal modulation［J］.Applied Optics，2001，40（13）：2126－2131.

［3］ Luo Zhiyong，Chen Zhaohui，Gu Yingzi，et al.Fivebucket phase－shifting algorithm based on numerical simulation［J］.Acta Optica Sinica，2006，26（11）：1687－1690.罗志勇，陈朝晖，顾英姿，等.基于数值模拟的高准确度五步相移算法研究［J］.光学学报，2006，26（11）：1687－1690.

［4］ Jun－ichi K，Lchirou Y.Phase－shifting fringe analysis for laser diode wavelength－scanning interferometer［J］.Optical Review，2000，7（2）：158－163.

［5］ Shan Xiaoqin，Zhu Rihong，Li Jianxin.Phase extraction for single frame interferogram based on 2DFourier transform［J］.Journal of Applied Optics，2013，34（5）：802－808.单小琴，朱日宏，李建欣.基于二维傅里叶变换的单帧干涉图相位提取方法［J］.应用光学，2013，34（5）：802－808.

［6］ Hao Q，Zhu Q D，Hu Y.Random phase－shifting interferometry without accurately controlling or calibrating the phase shifts［J］.Optics Letters，2009，34（8）：1288－1290.

［7］ Liu Dong，Yang Yongying，Tian Chao，et al.Study on phase retrieval from single close fringe pattern with high precision［J］.Chinese Journal of Lasers，2010，37（2）：531－536.刘东，杨甬英，田超，等.高精度单幅闭合条纹干涉图相位重构技术［J］.中国激光，2010，37（2）：531－536.

［8］ Hui Mei.Study on the theory and algorithms of phase－stepping interferometry［D］.Xi’an：Xi’an Institute of Optics and Precision Mechanics of CAS，2001.惠梅.表面微观形貌测量中相移干涉术的算法与实验研究［D］.西安：中国科学院西安光学精密机械研究所，2001.

［9］ Kamel H，Frederic C.Two－wavelength interferometry：extended range and accurate optical path difference analytical eatimator［J］.J.Opt.Soc.Am.A，2009，26（12）：2503－2511.

［10］Warnasooriya N，Kim M K.LED－based multi－wavelength phase imaging interference microscopy［J］.Optics Express，2007，15（15）：9239－9247.

［11］Christopher J M，Philip R B，Vincent C P.Quantitative phase imaging by three－wavelength digital holography［J］.Optics Express，2008，16（13）：9753－9764.

［12］Nilanthi W，Myung K K.Quantitative phase imaging using three－wavelength optical phase unwrraping［J］.Journal of Modern Optics，2009，56（1）：67－74.