一种受端电网限制短路电流的 多目标决策方法
朱 峥
(广东电网有限责任公司电力调度控制中心,广州 510000)
随着我国电网的快速发展,用电负荷迅速增加,电网规模不断扩大,500kV 主干网架已初步形成。然而由于500kV 电网与220kV 电网电磁环网运行,负荷相对集中,电网结构紧密,电源分布密集等原因使得电网的短路电流水平迅速增大,已严重影响到了整个电网的安全稳定运行,部分电网的短路电流已经逼近甚至可能会超过断路器的额定遮断容量,需采取有效措施进行电流限制。
实践证明,受端电网线路开断相对简单易行,而且短路电流的限制效果也很显著,并得以广泛应用。然而,通常的做法都是直接开断超标站点的出线,通过减少节点处注入短路电流的支路来降低该处节点的总电流,实际上这种做法仅仅是达到了局部电流的优化效果,但并没有考虑到系统的全局性。如何在满足短路电流的限制效果显著的同时,来尽量保持主网的完整性和系统的安全性,目前尚未提出有效的多目标决策方案[1-6]。
因此,本文提出了一种受端电网限制短路电流的多目标决策方法,能获得受端电网中限制各个超标站点的短路电流的最优断线组合,满足短路电流的限制效果。
1 受端电网限制短路电流的多目标决策方法
1.1 形成开断线路后的阻抗矩阵
通过计算获取所述受端电网的各个站点的自阻抗矩阵;开断所述受端电网任一超标站点k的m回线路,根据开断线路后的受端网络的注入电流和节点电压的关系(即U=ZI,其中,U为节点电压,Z为线路阻抗,I为注入电流),以及电流的变化量,对所述超标站点k的自阻抗矩阵Zkk进行更新,获得网络更新后的超标站点k的自阻抗矩阵Z′kk;其中,1≤k≤n。
1.2 求取自阻抗灵敏度
根据网络更新后的超标站点k的自阻抗矩阵Z′kk的各个对角线元素的变化,获得任意1 回开断线路的自阻抗灵敏度
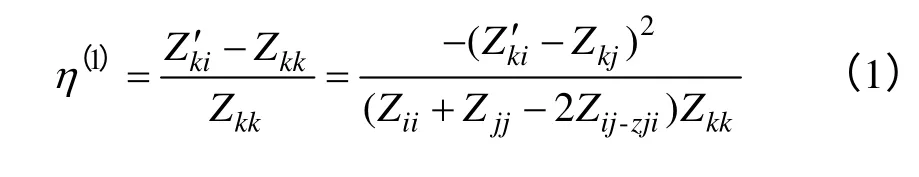
式中,i、j分别为所述任意1 回开断线路两端之间的开断节点;Zkk、Zkj分别为开断节点i、j与超标站点k的互阻抗矩阵;Zii、Zjj、Zkk分别为开断节点i、开断节点j超标站点k的自阻抗矩阵;Zij为开断节点i与开断节点j的互阻抗矩阵;Zij为开断节点i与开断节点j之间的开断线路的线路阻抗矩阵。
计算出所述超标站点k存在m回开断线路时的自阻抗灵敏度

所述受端网络存在n个超标站点,将所有超标站点的开断线路的自阻抗灵敏度进行叠加:
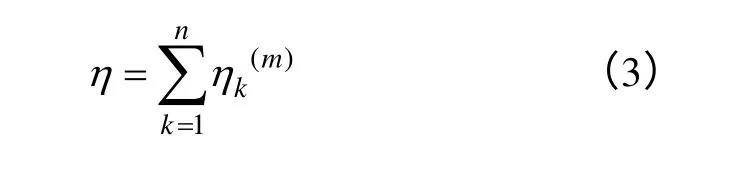
获得n个超标站点的自阻抗灵敏度η。
根据各个超标站点的实际短路电流和各个超标站点开关的遮断电流,获得各个超标站点的自阻抗灵敏度的权重系数

式中,参数Ik是第k个超标站点的实际短路电流;参数Ikb是第k个超标站点开关的遮断电流。
利用所述各个超标站点的自阻抗灵敏度的权重系数εk,对各个超标站点的自阻抗灵敏度进行加权,获得任一开断线路对受端电网所有超标站点的限制短路电流的加权自阻抗灵敏度
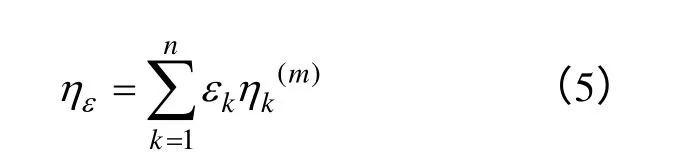
通过式(5)计算获得的参数ηε考虑了受端网络的各个超标站点的超标程度差异性影响,反映某一开断线路措施对限制电网所有超标站点的短路电流的加权自阻抗灵敏度。
1.3 求解潮流方程
运用牛顿-拉夫逊法求解获得所述受端电网的牛顿潮流修正式为

式中,J为雅可比矩阵;ΔU为牛顿迭代过程中的电压变化量,ΔW为功率偏差量和电压平方偏差量。具体实施时,判断所述受端电网的PV(有功功率P和电压幅值V)节点是否无功越界;若是,则将PV(有功功率P和电压幅值V)节点转化为PQ(有功功率P和无功功率Q)节点重新计算潮流,否则直接对牛顿潮流修正式(6)进行解算。
对式(6)进行解算后,可以获得所研究节点(即超标站点)的电压实部eL和虚部fL。
设ΔPL′与ΔQL′为负荷有功和无功的增量,式(6)两边分别对ΔP′L与ΔQ′L求导,可得基态网络的节点电压和电压灵敏度。例如:式(6)两边对 ΔPL′进行求导获得

则利用式(7)可以确定负荷节点(超标站点)的电压实部、虚部对自身有功功率微增量的灵敏度:同理,可以求得节点电压实部、虚部对自身无功功率微增量的灵敏度
可以定义一个参量为负荷裕度值λ,并且式(6)两边分别对负荷裕度值λ进行求导,从而获得基态网络的各种灵敏度。
首先,对式(6)两边求取负荷裕度值λ的一阶导数,方程如下:

再根据下面式(9)求取负荷裕度值λ的二阶 导数:
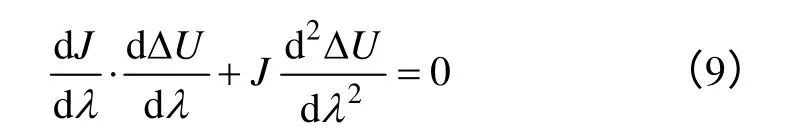
可以利用基态网络的节点电压和灵敏度等参数,获取非基态的节点电压和灵敏度参数。 所述静态电压稳定裕度的边界条件为

式中,PLk是受端网络中负荷节点L与超标节点k之间的有功功率;Rk是超标节点k的电阻值;QLk是负荷节点L与超标节点k之间的无功功率;Ek是超标节点k的电压值;Xk是超标节点k的电抗值;Zk是超标节点k的阻抗值。
则,最大负荷裕度λkcr与所述戴维南等值参数之间的关联关系为
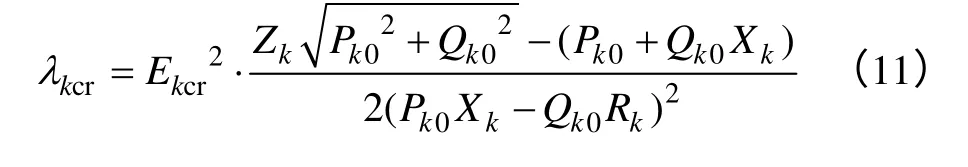
式中,Ekcr是超标节点k的最大电压值;Pk0是超标节点k与基态节点之间的有功功率;Qk0是超标节点k与基态节点之间的无功功率;并且,将所述最大负荷裕度λkcr的最小值λkcr=min(λkcr)作为开断线路对系统安全性的灵敏度指标。
1.4 多目标决策模型
在建立多目标模型时,将灵敏度(即参数η、ηε、λcr)视为函数值y,将影响灵敏度(η、ηε、λcr)的因子视为(决策)变量x,建立关系式y=f(x)。由于参数η、ηε、λcr的量纲不一致,因此,可以选取任意两个参量建立多目标模型后,再进行多目标最优化求解,从而获得在同一约束条件下,各个参量均有对应的最优解,即各个灵敏度均可达到最优值,从而可以选择相应的开断线路决策使得受端电网的性能得到综合最优。
2 算例分析
分别将所述加权自阻抗灵敏度ηε以及所述灵敏度指标λcr作为目标空间Y的单目标函数;x为目标空间Y中的各个单目标函数的影响因子,并且,各个单目标函数的影响因子x作为决策变量,且形成决策空间X。
将在目标空间Y中的所述加权自阻抗灵敏度ηε以及所述灵敏度指标λcr转化为多目标模型:

其中,f1(x)是目标空间Y中指代所述自阻抗灵敏度ηε的单目标函数;f2(x)是目标空间Y中指代所述自阻抗灵敏度ηε的单目标函数;g(x)≤0 是多目标模型y=f(x)的约束条件;g1(x),g2(x),…,gm(x)是各个单目标函数的组合约束条件,m≥1。g(x)≤0 为不等式约束条件,决定决策变量可行的取值范围。
将所述多目标模型y=f(x)转化为单目标函数:

其中,σ为多目标模型y=f(x)组合权重因子,且σ≥0,借助σ乘子,把该多目标模型y=f(x)=f1(x)+σ f1(x)。
对单目标函数y=f(x)=(f1(x)+σ f1(x)),即式(13)进行归一化处理:
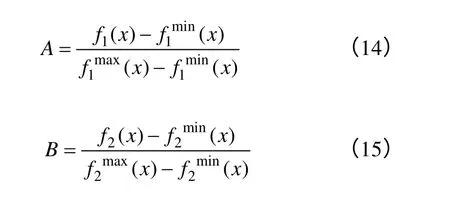
根据上式可知,当A,B∈[0,1],并且所求得的数值越接近零,则式(13)的单目标函数的优化效果越好。
将归一化处理获得参量A和B构成A-B曲线,并计算A-B曲线上的点距离原点的归一化欧氏 距离

由于A2≥0,B2≥0,则归一化欧氏距离D最小时,D2亦最小,那么式(12)最优解的求解问题可转化为:寻找一个最佳σ=σ**,使其对任意σ≥0 都有以式(13)为目标函数的最优模型的解对应的D2最小的问题。
将所述A-B曲线上参数A=B处的f1(x)与f2(x)的比值作为所述组合权重因子σ的初值σ(0)。
具体地,当A=B时,根据式(14)和(15),可以获得
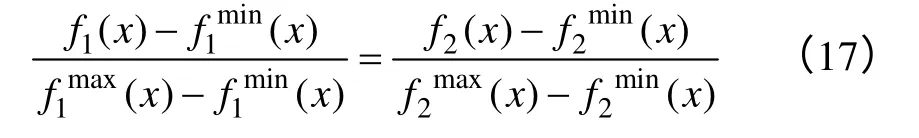
因此,将所述初值σ(0)作为σ的最优值对f(x)=f1(x)+σ f2(x)进行更新,对更新后的f(x)=f1(x)+σ(0)f2(x)进行求解,从而获得多目标模型y=f(x)的最优解。
3 结论
采用本文提出的受端电网限制短路电流的多目标决策方法,可以根据在线短路电流计算结果自动筛选出短路电流超标的母线或线路,不需要对所有开断线路组合进行短路电流校验计算,只需要根据开断部分(m回)线路由小到大的顺序进行检验即可,很大程度地提高了符合限流效果方案的选择速度,实现基于受端电网开断线路的限制超标短路电流的多目标方案的快速优化选择。本文提出的受端电网限制短路电流的多目标决策方法,可以在满足短路电流的限制效果和保持系统的完整性及安全性的综合效果最佳的多目标决策要求下,快速地寻找 到限制超标点短路电流的最优断线组合。综上可知,该方法实用性强,且易于实现,具有很高的实用价值和应用推广前景。
[1] 熊玮,夏文龙,余晓鸿,等.多核并行计算技术在电力系统短路计算中的应用[J].电力系统自动化,2011,35(8): 49-52,86.
[2] 熊中行.基于图形界面的电力系统短路计算[J].中国电力教育,2006,20(S3): 94-96.
[3] 朱寰,刘国平.江苏220kV 电网及限制短路电流的探讨[J].华东电力,2005,33(5): 34-37.
[4] 蔡广林,曹华珍.广东电网限制短路电流措施探讨[J].南方电网技术,2011,5(1): 90-94.
[5] 陆建忠,张啸虎.加强电网规划,优化电网结构,限制短路电流[J].华东电力,2005,33(5): 7-10.
[6] 何仰赞.电力系统分析[M].武汉: 华中科技大学出版社,2002.

