电磁脉冲作用下单极子天线的超宽带响应
肖卫东,刘义,熊波,刘其凤
(1.海军驻沪东中华造船(集团)有限公司军事代表室,上海 200129 2.电磁兼容性重点实验室,中国舰船研究设计中心,武汉 430064)
单极子天线广泛应用于短波和超短波通信系统,特别是近距离和编队间通信中。在当前电磁环境趋于复杂、干扰源不断增加的形势下,通信系统对干扰源特别是有意干扰源更为敏感。
有意电磁干扰的定义为:“有意产生电磁能量使得电子系统出现混乱、误操作,甚至是损毁电子设备”[1]。这种有意的电磁干扰能量可以通过非爆炸,甚至可以用高功率的超宽带系统产生[2]。
有意电磁干扰通常按以下方式影响通信系统:高功率或超宽带电磁干扰能量,通过直接辐照或感性、容性耦合等方式,进入天线、金属外壳以及传输线网络;继而在系统内部感应出高电压、电流,并导致器件内部的热或热应力快速上升,最终可能造成电路电热击穿,甚至是系统毁伤[3]。
对于通信系统与有意电磁干扰源的耦合分析,首先应关注干扰源和天线系统间的辐射直接耦合。时域分析方法能有效处理天线特征的宽带和非线性响应,被广泛运用于解决天线的瞬态散射和辐射问题,特别是基于时域步进(MOT)的TD-EFIE方法。MOT方法存在一定的不稳定问题,文献[4—6]给出了解决这一问题的方法。最近,基于拉盖儿多项式的阶数步进(MOD)的时域积分方法引起广泛关注[7—10]。该方法可以消除TD-EFIE方程中的时间变量和时间微分算子,但会增加编程计算的复杂程度。
文中将给出基于MOD方法的时域积分方程,该方法能有效求解通信用单极子天线的宽带响应。
1 脉冲分析理论
1.1 时域积分方程
金属表面的散射场可以表示为:

其中磁场矢量定义为:

标量电位定义为:


1.2 基于拉盖儿多项式的阶数步进积分方程法

未知量en,j可以表示阶数的和,然后任意时刻的电流密度可以表示为:

最后,由此可获得馈源处的电压量。
1.3 有意电磁干扰源信号
文献[11]对高功率电磁信号进行了研究,如图1所示。根据文献[11]中的实验数据,利用曲线拟合的方法可以到辐射场的解析表达式为:


图1 高功率电磁脉冲环境时域波形Fig.1 The time-domain waveform of high power electromagnetic pulse environment
系数 Ei,ti,wi可通过拟合法获得。
再假设电磁脉冲可能为快变、中变或者慢变波形[12],则高功率电磁脉冲波形可由式(14)表示:

2 数值结果和分析
利用文中的数学处理方法,可分析超短波单极子天线在外界电磁脉冲作用下的响应。首先为验证编写代码的正确性,计算了单极子天线馈电处的感应信号,并和试验结果进行了对比,如图2所示。图2中显示仿真结果和测试数据吻合较好,验证了所采用分析方法的正确性。

图2 测试和仿真数据对比分析Fig.2 The comparison analysis of test and simulation data
建立有限大小地面上单极子天线的模型,如图3所示。天线高度H=280 cm,天线半径r=0.6 cm,有限地面尺寸L=600 cm。

图3 电磁脉冲环境下单极子天线耦合响应Fig.3 The coupling response of single pole antenna in electromagnetic pulse environment
天线馈源出耦合的瞬态感应电压波形如图4所示。假设入射信号幅度E0=50 kV/m,为垂直极化入射,代入式(13)所示的电磁脉冲波形,进而考虑快变、慢变以及中度变化脉冲在天线馈源出产生的感应电压,并将响应结果进行对比。

图4 天线馈源处耦合的瞬态感应电压波形Fig.4 The coupling transient induced voltage waveform at the antenna feed
单极子天线端口馈源处产生的瞬态耦合电压如图5所示,响应的时域响应的频域特性曲线如图6所示。可以很明显看出,快变电磁脉冲在时域和频域都能感应出最强的耦合电压。由此可知,快变脉冲对与天线的辐射耦合能力最强。
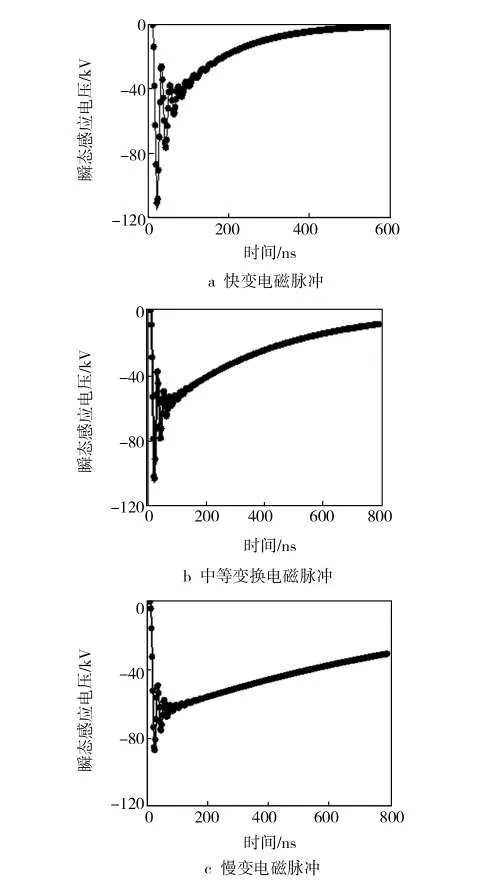
图5 天线馈源处耦合的瞬态感应电压波形Fig.5 The coupling transient induced voltage waveform at the antenna feed

图6 天线馈源处耦合的感应电压的频谱曲线Fig.6 The coupling introduced voltage frequency spectrum curve in antenna feed
3 结语
文中将拉盖尔多项式作为时域基函数,引入到基于RWG空间基函数的时域积分方程的求解中。利用该方法给出了预估天线瞬态响应的数值分析结果,并和试验数据进行了对比分析,验证了该方法的有效性,进而分析了不同输入脉冲参数变化对天线响应的影响。文中的分析方法可为天线或系统对外界有意电磁干扰的响应及防护研究提供输入条件。
[1] GIRI D V,TESCHE F M.Classication of Intentional Electromagnetic Environments(IEME)[J].IEEE Trans Electromagn Compat,2004,46(3):322—328.
[2]SABATH F,BACKSTROM M,NORDSTROM B,et al.Overview of four European High-power Microwave Narrow-band Test Facilities[J].IEEE Trans Electromagn Compat,2004,46(3):329—334.
[3] XU J F,YIN W Y,MAO J F,et al.Thermal Transient Response of GaAs FETs under Intentional Electromagnetic Interference(IEMI)[J].IEEE Trans Electromagn Compat,2008,50(2):340—346.
[4] RAO S M,SARKAR T K.An Alternative Version of the Time Domain Electric Field Integral Equation for Arbitrarily Shaped Conductors[J].IEEE Trans Antennas Propag,1993,41(6):831—834.
[5]MANARA G,MONORCHIO A,REGGIANNINI R.A Spacetime Discretization Criterion for a Stable Time-marching Solution of Electric Field Integral Equation[J].IEEE Trans Antennas Propag,1993,45(3):527—532.
[6] WEILE D S,PISHARODY G,CHEN N W,et al.A Novel Scheme for the Solution of the Time-domain Integral Equations of Electromagnetics[J].IEEE Trans Antennas Propag,2004,52(1):283—295.
[7]JUNG B H,CHUNG Y S,SARKAR T K.Time-domain EFIE,MFIE and CFIE Formulations Using Laguerre Polynomials as Temporal Basis Functions for the Analysis of Transient Scattering form Arbitrarily Shaped Conducting Structures[J].Progress Electromagn Res,2003,39:1—45.
[8] CHUNG Y S,SARKAR T K,JUNG B H,et al.Solution of Time Domain Electric Field Integral Equation Using the Laguerre Polynomials[J].IEEE Trans Antennas Propag,2004,52(9):2319—2328.
[9] JI Z,SARKAR T K,JUNG B H,et al.Solving Time Domain Electric Field Integral Equation without the Time Variable[J].IEEE Trans Antennas Propag,2006,54(1):258—262.
[10]JI Z,SARKAR T K,JUNG B H,et al.A Stable Solution of Time Domain Electric Field Integral Equation for Thin-wire Antennas Using the Laguerre Polynomials[J].IEEE Trans Antennas Propag,2004,52(10):2641—2649.
[11]BENFORD J,SWEGLE J A,SCHAMILOGLU E.High Power Micrwaves[M].Florida:CRC Press,2007.
[12]LIU Q F,YIN W Y,XUE M F,et al.Shielding Characterization of Metallic Enclosures with Multiple Slots and a Thin Wire Antenna Loaded:Multiple Oblique EMP Incidence with Arbitrary Polarization[J].IEEE Trans Electromagn Compat,2009,51(2):284—292.

