谐波对电流互感器误差的影响
冯 昊
(中钢集团武汉安全环保研究院,武汉 430081)
电力系统的谐波问题早在20 世纪20年代就引起了人们的注意,到了60年代由于高压直流输电技术的发展,大量关于变流器引起电力系统谐波问题的文章被发表。70年代以来,由于电力电子技术的飞速发展,各种电力电子装置在电力系统、工业、交通及家庭中的应用日益广泛,谐波所造成的危害也日趋严重。谐波使电能的生产、传输和利用效率降低,使电气设备过热、产生振动和噪音,并使绝缘老化,使用寿命缩短,甚至发生故障或烧毁。谐波可引起电力系统局部并联谐振或串联谐振,使谐波含量放大,造成电容器等设备烧毁,还会引起继电保护和自动装置误动作,使电能计量出现混论。对于电力系统外部,谐波对通信设备和电子设备会产生严重干扰[1-3]。
对电网中谐波的监测的一般以监测仪表为核心,用安装了管理软件的电脑作为主站,通过有线(RS232/485)和网络(RJ45)将监测数据采集后进行分析处理。这里的监测仪表主要为电流传感类设备,然而对于此类设备自身受谐波影响的程度,目前的检测工作难度较大,首先是因为含有各种谐波分量的大型电流源制作难度大、造价高,其次是谐波电流测量系统本身的溯源方法及测量不确定度评估在技术上的难度较大[4-6]。
本文以电磁式电流互感器为例,根据等安匝原理将含有高次谐波的电流通入被测电流互感器,将其输出作为测量信号与没有通过电流互感器变化的一次叠加信号进行比较,分析在谐波干扰下电流互感器误差的变化情况。由于普通互感器校验仪原理的限制,使得其同样受到谐波的影响,所以本次分析使用可以进行宽频采集的数字采集卡完成。该方法在一定程度上使得谐波电流测量的溯源方法和测量系统的不确定度评估变得简单。
1 测量系统的设计
测量系统如图1所示,由测量通道、参考通道和分析平台三部分组成。和表示工频电流源和高次谐波电流源,I˙1和I˙2表示工频电流和高次谐波电流,CTX为被测电流互感器,a 和b 端子表示电流互感器的二次输出端子,在标准电阻RX上产生测量电压信号进入测量端口CH1。没有参与电流互感器转化的电流信号分别通过标准电阻R1和R2转化后叠加形成参考电压信号进入参考端口CH0。被测电流互感器选择电力系统常规电流互感器,准确度等级为0.2 级,测量系统应高于电流互感器至少2 个等级,达到0.05 级的水平。测量系统的误差来源主要包括标准电阻和A/D 转换卡,即


图1 测量系统示意图
参考通道上含有两个标准电阻器,所以标准电阻器选择0.02 级即可,这个等级的电阻器很容易采购。那么A/D 转化部分的准确度等级至少要达到0.01 级的要求。数字采样的最大误差可表示为

式中,Δ表示为在允许误差数值范围内的最大电压值。假设所使用的A/D 转换卡为N-bit,那么最大的允许电压Δ可表示为:

式中,Umax为N-bit 的A/D 转换卡的最大允许输入电压值。一般A/D 卡的最大输入电压值为10V。电力系统上使用的电流互感器的输出一般为 1A 或5A,这里选择二次输出为5A 的电流互感器作为被测对象,RX为0.8Ω,系统输入电压值为4V,那么A/D 转换卡的误差可以表示为[7]

结合式(2)至式(4)可以计算出在电流互感器5%~120%的额定电流下A/D 转换卡带来的误差情况。经过计算得到18bit 的A/D 转换卡在5%额定电流下产生的误差δA/D(5%)=0.01%,在120%额定电流下产生的误差δA/D(120%)=0.004%,满足A/D 转换卡的准确度等级要求,但实际应用过程中转化卡通常不能达到它的理论计算值,所以本系统选择20-bit 的A/D 转换卡。
由于试验用电流互感器是在叠加了高次谐波的基波电流下工作,其输出含有谐波成分,所以选择的算法必须可以准确的从基波信号中分析出不同的谐波信号,而传统的FFT 算法在频率变化的情况下不能满足要求。提高对高次谐波的分析能力,实质上是在某种程度上减少栅栏效应和频谱泄露。DFT是一种时域和频域均离散化的变换,可以对连续时间信号的傅里叶变换进行逼近,进而分析连续时间信号的频谱。本次试验的程序采用了离散傅里叶变换(DFT)算法[7-9]。DFT 的定义为:设有限长序列x(n) 长为N(0≤n≤N-1),其离散傅里叶变换是一个长为N的频率有限长序列(0≤k≤N-1),其正变换为
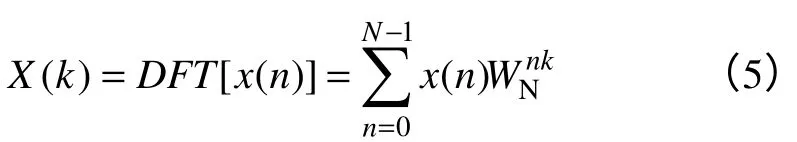
DFT 的实质是把有限长序列当作周期序列的主值序列进行DFT 变换,x(n)、X(k)的长度均为N,都是独立值,因此二者具有的信息量是相等的。已知x(n)可以唯一确定X(k),已知X(k)可以惟一确定x(n)。分析软件的算法流程图如图2所示。
2 电流互感器误差模型的建立
CT的等效电路如图3所示,图中:Z1、Z2、ZL、Ze分别为CT的一次折算二次的阻抗、二次阻抗、二次侧负载阻抗和励磁阻抗;i1、i2、ie分别为折算到二次侧的一次电流、二次电流和励磁电流;E为励磁阻抗上的感应电动势。

图2 分析软件的算法流程图

图3 CT 等效电路
在谐波干扰情况下,主磁链出现谐波分量,谐波分量和基波分量产生的励磁磁通进行叠加,形成干扰后的总磁通密度。对于计量用CT稳态传变特性的影响主要用比值差f和相位差δ来衡量,二者皆基于电流的基波分量进行定义。电流互感器由于励磁电流I0的存在,使得乘以匝数比后的二次电流不仅数值与一次电流I1不等,而且相位也产生了差异,也就产生了误差ε,即


Zb为二次回路总阻抗Zb=Z2+Z;B为磁通密度;H为磁场强度;Ac为铁心有效截面积;Lc为铁心的平均磁路长;μ为铁心材料的导磁率;N1为额定一次匝数;N2为额定二次匝数。
通过误差公式可知,当存在高次谐波电流时,产生的磁通导致铁心磁导率下降,励磁电流增加,使原有误差曲线向负方向偏移。由于电网一次电流不受电流互感器变化的影响,高次谐波分量的增加,使得二次感应电势的基波成分比无高次谐波情况下相对减少,因此造成比差向负方向变化,角差向正方向变化。
3 验证试验
试验用电流互感器为110kV 线路中常规电流互感器,电流变比为600A∶5A,准确度等级为0.2 级,铁心材料分别选择硅钢片和超微晶两种。在一次电流中分别叠加的3 次、5 次、7 次谐波,谐波含量为基波的1%。谐波源为定制高次谐波源,输出频率150~350Hz,输出容量5V,500A,电压稳定率<1%,波形失真率<2%。参考通道的取样电阻R1=R2=6.6mΩ,R1=R2确保了对于工频电流和高次电流的取样比例是一致的。试验数据如表1所示。编号1 号为硅钢片材料,编号2 号为超微晶材料。
根据表1的实测数据可知,当基波电流中叠加谐波分量后,电流互感器的比值差往负方向偏移,相位差往正方向偏移,并且这种趋势在150Hz 时最为明显,随着频率的增加,偏移量逐渐减小。这一现象与理论推导结论完全一致。对于硅钢片材料的铁心,在3 次谐波干扰下,5%点的变化最大,此时比值差减小了2.65 倍,相位差增大了0.34 倍;在120%点时这一变化为1.04 倍和0.14 倍。在7 次谐波干扰下,误差变化最大点为5%,此时比值差减小了0.65 倍,相位差增大了0.14 倍;在120%点时这一变化为0.38 倍和0.01 倍。对于超微晶材料铁心,在3 次谐波干扰下,5%点的比值差减小了6.19 倍,相位差增加了7.18 倍;在120%点比值差减小了0.11倍,相位差增加了0.06 倍。由0.2 级电流互感器的误差限值可知,在一次叠加1%的高次谐波时,硅钢片材料的电流互感器误差没有超过限值,而超微晶材料的电流互感器在受到150Hz 的干扰时所有测量点均超过该等级的误差限值。证明在相同谐波干扰情况下,硅钢片材料的改变相对较均匀平滑,超微晶材料的变化较剧烈。

表1 高次谐波干扰后测量数据
图4和图5为硅钢片材料受到不同谐波干扰后误差曲线变化,其中图4为比值差变化曲线,图5为相位差变化曲线。图6和图7为超微晶材料受到不同谐波干扰后误差曲线变化,其中6 为比值差变化曲线,图7为相位差变化曲线。
比较图4至图7可知,3、5、7 次谐波对硅钢片误差的影响基本是均匀的,7 次谐波下在5%的额定电流测量点时,其比值差于没有谐波干扰时的比值差近似相等,随着额定电流的升高,差别逐渐明显,在100%额定电流后比值差之间的差别近似不变。相位差除3 次谐波干扰下区别明显外,5 次和7次谐波对硅钢片材料的相位差改变并不明显,特别是在额定电流小的情况下。对于超微晶材料,3 次谐波对电流互感器误差的影响非常突出,当谐波次数升高到5 次时,影响量明显减小,当谐波达到7次时,其对电流互感器的误差影响几乎没有。证明在滤波效果上,硅钢片材料的电流互感器没有超微晶材料的电流互感器好。对于硅钢片材料而言,7次谐波依然可以穿过电流互感器而对其输出产生影响,而超微晶材料的电流互感器在遇见7 次及以上高次谐波后,这些谐波基本无法穿过,对电流互感器的输出几乎不产生影响。但当电网中存在3 次谐波时,超微晶材料受到的影响较硅钢片材料要敏感的多。

图4 硅钢片材料CT 比值差曲线

图5 硅钢片材料CT 相位差曲线
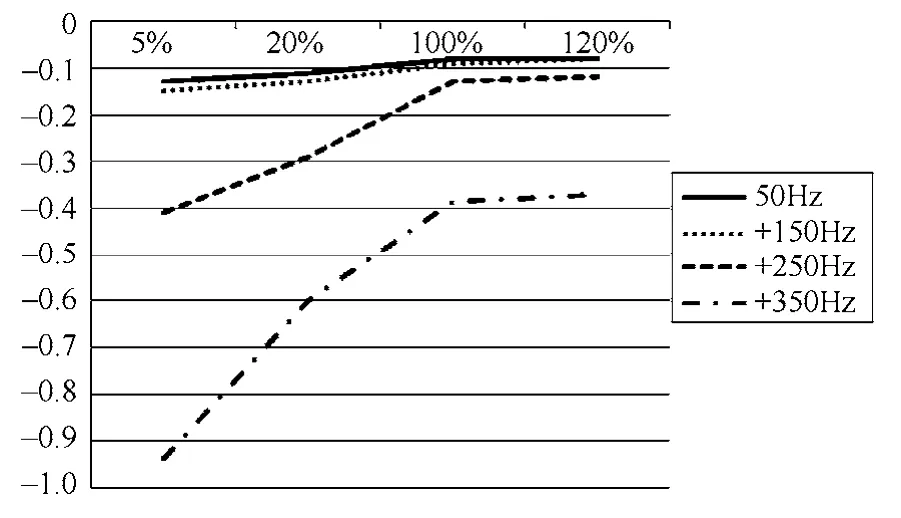
图6 超微晶材料CT 比值差曲线
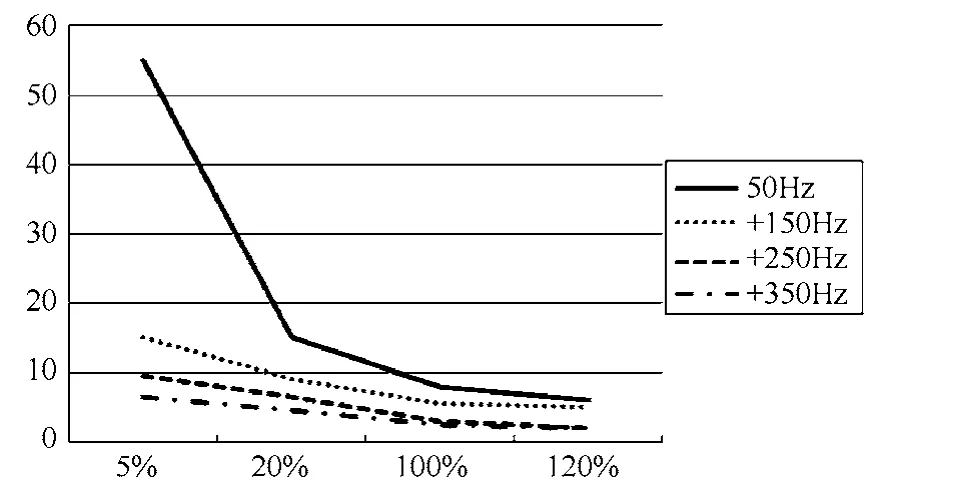
图7 超微晶材料CT 相位差曲线
4 结论
本文基于等安匝原理,通过理论分析和验证试验两方面对电磁式电流互感器进行了谐波干扰下误差特性的研究。由于常规互感器校验仪的原理所限,本文为了获得准确的误差数据,自制了一套高次谐波误差分析装置,该装置由测量通道、参考通道和分析平台三部分组成,并根据实际测量要求选择了合适的采集卡和分析算法。
文章最后给出了验证试验数据,可知高次谐波会加速互感器铁心饱和,使得电流互感器的比值差往负方向偏移,相位差往正方向偏移,且电网中的3 次谐波对互感器误差的影响最大。对于硅钢片材料的电流互感器,各次谐波对其误差的影响近似呈均匀分布,但对于超微晶材料的电流互感器,3 次谐波影响程度远高于其他谐波,且当谐波次数达到7 次后,超微晶材料显示出明显的滤波功能,使得7次及以上高频电流信号无法穿过电流互感器,从而使得7 次及以上高频电流不会对超微晶材料的电流互感器的误差产生影响。硅钢片材料的滤波效果没有超微晶好,7 次谐波对其误差依然产生明显的影响。
[1] Yazdani-Asrami M,Mirzaie M.Amir abbas shayegani akmal.investigation on impact of current harmonic contents on the distribution transformer losses and remaining Life[J].IEEE International Conference on Power and Energy,2010,29(1): 689-694.
[2] Elmoudi A,Lehtonen M,Nordman H.Effect of harmonics on transformers loss of Life[C]//Conference Record of the 2006 IEEE International Symposium on Electrical Insulation,2006: 408-411.
[3] 肖雁鸿,毛筱,周靖林,等.电力系统谐波测量方法综述[J].电网技术,2002,26(6): 61-64.
[4] Cataliotti A,Di Carad,Emanuel A E,et al.Current transformers effects on the measurement of harmonic active power in LV and MV networks[J].Power Delivery,IEEE Transactions on,2011,26(1): 360-368.
[5] Cataliotti.A,Di Cara.D,Emanuel.A.E,et al.Characterization of Current Transformers in the Presence of Harmonic Distortion [J].Instrumentation and Measurement Technology Conference Proceedings,2008.IMTC 2008.IEEE.2008: 2074-2078.
[6] 于淼,张炳达.配电网中谐波源检测方法的研究[J].电力系统及其自动化学报,2005,17(1): 36-40,87.
[7] Zhang Zhi,Li Hong-bin.An accurate system for onsit calibration of electronic transformers with digital output [J].Review of Scientific Instrument,2012,83(6): 065111-065111-7.
[8] 曹团结,张剑,尹项根,等.电流互感器的误差分析与工程计算[J].电力自动化设备,2007,27(1): 53-56.
[9] 李长云,李庆民,李贞,等.直流偏磁条件下电流互感器的传变特性[J].中国电机工程学报,2010,30(19): 127-131.
[10] 李春来,汤晓宇,黄业安,等.计量用TA 在直流偏磁条件下传变特性的实验与分析[J].电力自动化设备,2011,31(7): 143-145,149.

