基于组合效应分析的工程分标决策模型研究

刘 迅，王宇静，张 怡，毕远志

(1.江南大学 环境与土木工程学院，江苏 无锡214122;2.上海工程技术大学 管理学院，上海201620;3.河海大学 工程管理研究所，江苏 南京210098)

大中型建设工程项目，尤其是交通、水利项目，合理地划分标段是项目成功的关键因素之一。合理的建设工程标段划分能够使业主缩短建设工期，降低工程建设风险［1］，降低建设工程交易费用，使工程总费用达到最优，从而有利于实现工程项目投资控制优化的目标［2-5］，但是当所分的标段过多时，又容易增加界面管理的难度。采取何种分标决策办法对整个工程进行有效的标段划分，从而谋取最佳的经济技术效果，成为业主和相关专业人士共同关注的问题。

目前，许多学者对建设工程标段划分的问题进行了有益的探索。GONZÁLEZ -DÍAZ 等指出业主为了节省其自身内部作业或当地劳力资源及监控方面所需要的费用与时间，可将工程予以分标发包［6］。张利荣定性分析了工程项目建设成本与标段数之间的关系，不同的标段划分方案其成本不同的主要原因是组成标段的子项目之间的相关关系［7］。申玲等以交易费用为理论工具，分析了DBB 模式下合理的标段划分和合同激励问题。张智慧等从业主角度出发，强调业主在划分标段确定标段数量时应充分考虑标段划分对总的工程造价的影响［8］。洪伟民等从交易费用理论出发，建立建设工程标段划分优化模型，并提出用蒙特卡洛方法对模型进行求解的思路。孟碟等以云南盈江滚朋羊二级水电站工程标段划分为背景，从经济学的角度构建了施工总成本数学模型，并详细分析了该模型与标段划分的经济技术关系［9］。张利荣等基于项目是多个子项目聚合集的视角，构建了标段划分的数学模型，分析了子项目粒度对标段划分方案的巨大影响，指出标段划分时要科学地确定子项目粒度，给出了标段划分的多目标优化模型和3 种典型的单目标优化模型，并探讨了标段划分优化模型的求解方法［10］。以上对建设工程标段划分的研究，较多基于实际工程经验，以定性分析为主，缺乏有力的定量分析方法与实践。

事实上，建设工程一般都按一定的规则细分为若干个子项目，例如水利水电工程按层级划分为单位工程、分项工程与单元工程3 级。建设工程中发包方考虑工程分标时，一般是将这些单位工程与分部工程作为子项目，但是在这些不同的单位工程与分部工程之间存在着很多复杂的组合方式，发包方对建设工程项目的分标工作一般都是根据经验进行的，显然这有很大的缺陷。针对这些不足，笔者在分标约束条件下提出建设工程业主方的分标决策目标，即选择技术实力强、管理水平高的施工队伍;招标工程标段划分要尽可能有利于工程施工，有利于降低工程交易费用，有利于实现工程总费用最优［11-12］。

1 工程分标决策基本模型的构建

1.1 模型定义

定义1 如果一个子项目集合K中任意一个标段a，及任意两个不包含a的子项目组合S和T，S⊂T，则有式(1)成立：

可称这些子项目对分标专家i来说具有组合效应，若所有参与分标的专家都有式(1)成立，则称这些子项目是具有组合效应的子项目。

这说明，专家认为子项目之间具有组合效应，若再添加一个子项目，其所增加的效用会随着已获得的子项目数目的增加而增加。式(1)也等价于式(2)：

特别地，若S∩T=∅，那么：

这说明对专家来说，这些标段是具有组合效应的子项目。

假设有K个具有组合效应的子项目和N个专家。专家对每个子项目都有自己的私人估值，这些估值与专家自己的偏好类型θi有关，不妨用Wi(S，θi)表示专家i(i=1，2，…，N)的估值函数，其中S是任意子项目组合。专家的偏好类型是其私人信息，其他专家都无从得知，但专家的偏好类型的分布是共同知识，不妨假设θi(i=1，2，…，N)在区间上服从分布Fi·()，其密度函数为fi(·)。

1.2 工程分标决策目标的构建

为求解简单，该研究考虑只有两个且有组合效应的子项目的情况。假设只有两个具有组合效应的子项目(j=1，2)，专家i对子项目1 的估值为(θi)，对子项目2 的估值为(θi)，对两个子项目组合的估值为(θi)+(θi)+(θi)，(θi)表示当两个子项目组合在一起时所带来的超额期望值(相对于单个子项目所带来的期望值的和)，并且是非负的，即(θi)≥0，表明两个子项目对专家i来说是具有组合效应的，因此(θi)可以看作是专家i对两个子项目之间组合效应的一个度量。进一步地，作出如下假设：

(2)对 所 有 的i，分 布 函 数Fi(·)满 足：

则专家i的期望值就可以简化为：

将式(5)代入到专家的目标函数，可得：

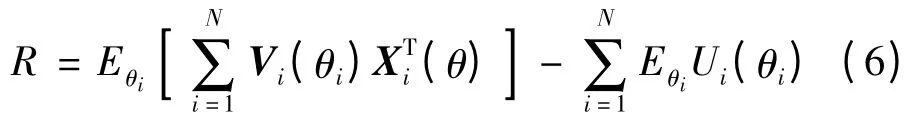
对于任意的i，xi(θ)关于θi是单调非减的，并且：

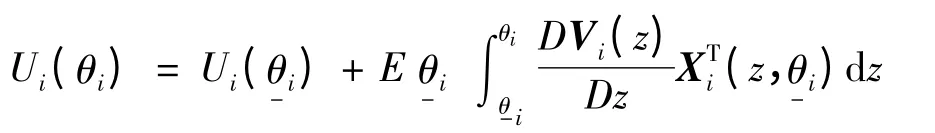
另外，对于所有专家的最低偏好类型都是紧的，即∀i，Ui(θ-i)=0。

依据积分交换公式，可得：

将式(7)代入式(5)，可得到专家的期望值为：

也可以写成式(8)：

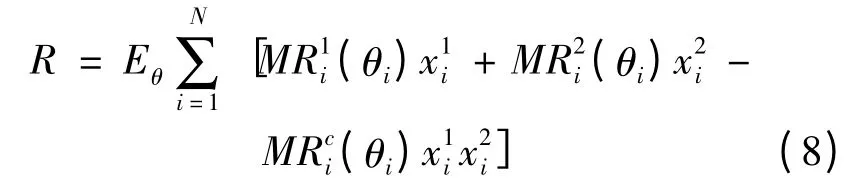
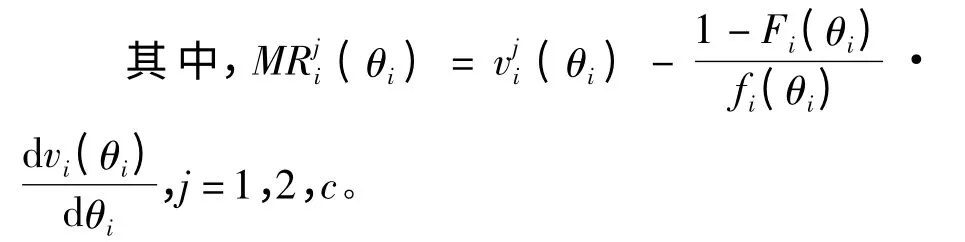
专家只要对(N+1)2种分配方式分别计算式(9)的值，取到最大值时的分配即为最优方案。

1.3 工程分标决策约束条件

式(8)中θi的取值是由影响工程分标的因素共同决定的，这些影响因素构成了工程分标的约束条件。GORDON 从工程项目的特点、业主方的能力与偏好和市场环境3 个方面分析了建设工程发包方式选择的影响因素［13］。MOHAMMED 将工程发包方式选择的影响因素分为项目特性、业主方的需求和业主方的偏好3 类［14］。IBRAHIM等从业主特性、项目特性、设计特性、法律法规、承包人特性、风险管理，以及索赔与争议7 个方面，列举了34 个影响建设工程发包方式选择的因素［15］。ALHAZMI 等从业主需求、项目特性、市场特性、承包人需求、当地的建筑法律法规、业主的类型，以及业主的设计组织7 个方面，列举了47个影响建设工程发包方式选择的因素［16］。文献［17］结合其他学者已有的研究成果，对工程分标的影响因素集做了分析，总结出14 个影响因素，在调查专家确定的基础上，设计出了一个专家问卷调查表，并对收回的调查数据进行了隶属度分析，紧接着进一步运用因子分析法对这些影响因素集进行了实证研究，结合碎石图和解释的总方差表，给出了工程分标影响因素集的成分矩阵，从而总结出了工程分标影响因素的4 个主成分，即市场因素、工程特点、工程期望和业主因素，并由此建立各个主要影响因素的权重。

2 决策模型

2.1 组合效应对工程分标的影响

假设参与建设工程项目发包方分标的专家对分标的估值函数具有线性关系，即：

假设所有专家对子项目组合效应程度的认识是相同的，且与专家的类型无关，即(θi)=c。

当两个子项目都分配给专家i时，招标人所获得的期望值为：

当子项目1 分配给专家j、子项目2 分配给专家k时的期望值为：

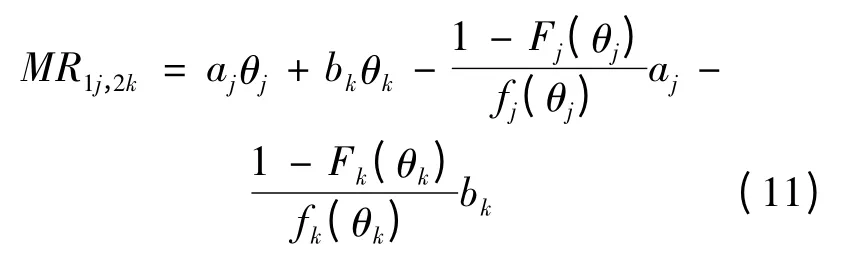
当子项目1 分配给专家k、子项目2 分配给专家j时的期望值为：

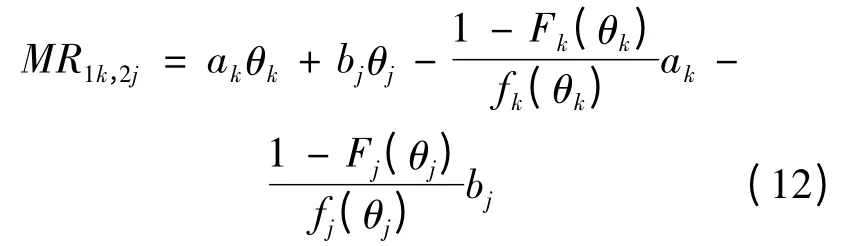
若子项目之间的组合效应c足够高，使得：

则子项目组合是最优的。

为了使上述结果更加清楚，可做进一步假设。假设只有两个专家且k2＞k1，θi(i=1，2)服从［0，1］上的均匀分布，则计算每种分配下专家所获得期望值为：

子项目i分配给专家i

当组合效应足够高，使c＞min{［(2θ2-1)k2-(2θ1-1)k1］，2(θ1-θ2)}时，子项目组合总是最优的。

2.2 工程分标决策模型的推广

假设有N个组合效应的子项目(j=1，2，…，N)，专家i对子项目1 的估值为(θi)，对子项目2 的估值为(θi)，对子项目N的估值为(θi)，对N个子项目组合的估值为(θi)+(θi)+… +为N个子项目组合在一起时给其带来的超额期望值(相对于单个子项目给其带来的期望值的和)，且是非负的，即(θi)≥0，表明N个子项目对专家i来说是具有组合效应的，因此(θi)可以看作是专家i对N个子项目之间组合效应的一个度量。进一步地，作出如下假设：

(2)对 所 有 的i，分 布 函 数Fi(·)满 足：

则式(8)可以推广成如下的公式：

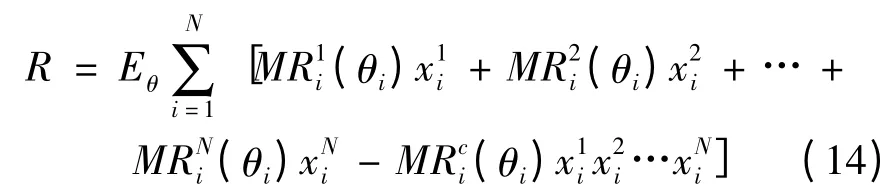
3 算例

某大型抽水蓄电站地下车库工程一般可分为3 个子项目，即开挖支护工程S1、混凝土工程S2和安装工程S3，分析在两个标段组合下工程项目发包方的分标决策模型。

3.1 工程分标方案集

方案集是实现决策目标的基础，只有获得能够实现目标的各种方案，并加以认真分析研究，才能得到科学的决策结果。理论上有{{S1，S2，S3}}，{{S1，S2}，{S3}}，{{S1}，{S2，S3}}，{{S1，S3}，{S2}}和{{S1}，{S2}，{S3}}5 种标段划分方案，如表1 所示。

表1 分标方案集

3.2 约束条件

由于工程特点、市场因素、工程期望和业主因素等分标约束条件，业主均不选择一个标段方案{{S1，S2，S3}}和3 个标段方案{{S1}，{S2}，{S3}}，而是选择分两个标段方案，即在{{S1，S2}，{S3}}，{{S2，S3}，{S1}}和{{S1，S3}，{S2}}中选择。

3.3 可行分标方案集的构建

在分析两个标段的3 个方案中，{S1}，{S2}和{S3}各成为一个标段均可行，故比较{S1，S2}，{S2，S3}和{S1，S3}3 个组合标段的优劣即可得出结论。对两个子项目进行组合，假设有6 位专家，这些专家的估值函数如表2 所示。

表2 专家的估值函数

其中，θi为专家i的偏好类型。θi的值与具体的标段无关，只与专家对投标公司经营能力估计、风险态度和知识经验等有关，不妨设分别取值：60，49，58，65，54，71。θi的取值是专家i的私人信息，其他专家只知道θi的分布，可以假设θi(i=1，2，…，6)都是服从［1，100］上的均匀分布。容易知道估值函数和分布函数是满足假设的。

首先，根据最优招标机制的分配规则，分别计算在各个分配方式下招标人的目标函数值：

同理可得：

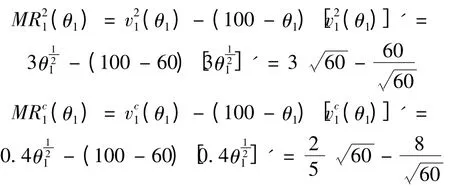
由此可得，专家1 对这两个子项目的组合估值为：

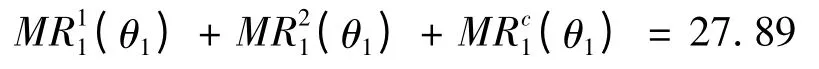
同理，可以计算出专家2 ～专家6 对这两个子项目的组合估值分别为18.80、25.75、25.34、18.98 和20.12。

4 结论

笔者在前人提出建设工程业主分段招标过程中需要考虑子项目组合效应的基础上，构建了子项目组合效应的建设工程分标决策模型，并提出了该模型下实施的可操作性步骤。针对建设工程项目标段划分的特点，分析了组合效应对子项目组合的影响，使整个决策目标更为完善，因而模型的有效性和实用性更强。此外，与现有研究成果相比，该研究成果具有更强的理论支撑，为建设工程发包方标段划分决策提供了一个一般性的分析框架。通过算例表明，此模型能够为分标决策者提供有力的支持。

［1］何倩儒. 高速公路标段划分与界面管理研究［D］.北京：清华大学图书馆，2009.

［2］申玲，张俊杰.基于交易费用分析的DBB 模式标段划分及合同激励［J］.建筑经济，2008(4)：114-116.

［3］洪伟民，王卓甫. 建设工程施工标段划分优化研究［J］. 武汉理工大学学报：交通科学与工程版，2010，34(2)：401 -404.

［4］王卓甫，丁继勇，周建春，等.基于机制设计理论的建设工程招标最优机制设计［J］.重庆大学学报：社会科学版，2013，19(5)：73 -78.

［5］王卓甫，杨高升，邢会歌.建设工程招标模型与评标机制设计［J］.土木工程学报，2010，43(8)：140-145.

［6］GONZÁLEZ -DÍAZ M，ARRUÑADA B，FERNÁNDEZ A. Causes of subcontracting：evidence from panel data on construction firms［J］. Journal of Economic Behavior＆ Organization，2000，42(2)：167-187.

［7］张利荣. 建设工程标段划分研究［J］. 水利水电技术，2006，37(7)：82 -84.

［8］张智慧，何倩儒. 高速公路标段划分对工程造价的影响［J］.清华大学学报：自然科学版，2010，50(6)：830 -833.

［9］孟碟，冯平. 滚朋羊二级水电站工程标段的优化划分［J］.天津大学学报，2011，44(12)：1088 -1092.

［10］张利荣，刘珩，张震.工程项目标段划分及其优化的数学模型［J］.水利水电技术，2012，43(12)：67-70.

［11］郑边江.建设工程最优招标机制的设计［J］. 科技进步与对策，2008，25(10)：53 -56.

［12］张怡，史峰.建设工程组合招标机制设计模型研究［J］.人民长江，2011，42(23)：102 -106.

［13］GORDON C M.Choosing appropriate construction contracting method［J］. Journal of Construction Engineering and Management，1994，120(1)：196 -210.

［14］MOHAMMED A. Selecting the appropriate project delivery method using AHP［J］. International Journal of Project Management，2002，20(6)：469-474.

［15］IBRAHIM M，ALRESHAID K.Decision support system for selecting the proper project delivery method using analytical hierarchy process (AHP)［J］. International Journal of Project Management，2005，23(7)：564-572.

［16］ALHAZMI T，MCCAFFER R. Project procurement system selection model［J］. Journal of Construction Engineering and Management，2000，126(3)：176-184.

［17］张怡.考虑交易费用的工程分标决策研究［D］.南京：河海大学图书馆，2012.