球床高温堆平衡态燃耗计算程序的开发

朱贵凤，邹 杨，李明海，严 睿，彭红花，徐洪杰，＊

（1.中国科学院 上海应用物理研究所，上海 201800；2.中国科学院 核辐射与核能技术重点实验室，上海 201800；3.中国科学院大学，北京 100049）

球床高温堆平衡态燃耗计算程序的开发

朱贵凤1，2，3，邹 杨1，2，李明海1，2，严 睿1，2，彭红花1，2，徐洪杰1，2，＊

（1.中国科学院 上海应用物理研究所，上海 201800；2.中国科学院 核辐射与核能技术重点实验室，上海 201800；3.中国科学院大学，北京 100049）

基于MCNP5和ORIGEN2耦合方法，开发了平衡态下球床高温堆的燃耗计算程序PBRE，用于堆的性能价值分析。为节省蒙特卡罗计算时间，对迭代收敛的方法进行优化，使之可在10个迭代步内收敛。使用PBRE对清华大学HTR-10进行建模计算，得到的平均卸料燃耗深度与文献报道值一致，表明PBRE程序适用于球床堆平衡态的燃耗分析。

球床堆；平衡态；燃耗；PBRE

近年来，球床高温堆因其具有较高的热转化效率及可实现高温制氢的潜在产业优势，受主要核大国的推崇。球床高温堆的一显著特点是在线换料，能实现较高的燃耗深度，因而具有较好的燃料利用率，但这种流动性也决定了其燃耗分析与以往的压水堆相比更困难。

早期的球床堆燃耗程序有VSOP［1］，其将时间项和空间项分开处理，各区间做完1次点燃耗计算后，再进行1次空间平移处理，以此完成区间滞留时间内的流动燃耗计算。由于对堆的性能价值评估只需分析堆平衡态时的燃耗深度等物理参数，随后的确定论球床堆燃耗程序大部分是基于平衡态而开发的，如PREC［2］和PEBBED［3］等。PREC只局限于计算1次通过的换料方式；而PEBBED考虑再循环燃料在入口的边界条件，使用双迭代计算，可适用于各种换料方案的设计。

为避免确定论方法的几何局限性和等效方法带来的误差，出现了基于蒙特卡罗方法开发的平衡态燃耗程序。2007年，Fratoni［4］在MOCUP程序的基础上开发了球床堆平衡态燃耗计算程序，根据全反射边界单球模型计算提供堆芯燃耗成分。但其关于滞留时间的修正方法以及程序准确性的基准验算未见相关报道。

本文根据PEBBED程序的思路，采用MCNP5和ORIGEN2耦合的方法，开发1套平衡态球床高温堆的燃耗分析程序PBRE。针对蒙特卡罗计算耗时的不足，重点对其收敛方法进行分析，以期稳定加速收敛，最后采用HTR-10堆芯进行程序验证。

1 程序设计思路

燃耗耦合程序需联合解中子输运、功率和燃耗3个方程。中子输运方程采用MCNP5求解，给出单群截面和相对中子注量率分布；功率方程解出源强并计算出实际的中子注量率；燃耗方程通过中子注量率和单群截面解出堆芯燃耗成分分布，供中子输运计算使用，整个迭代过程设为内迭代计算。为实现keff收敛到预期值，需不断修改换料方案，这个迭代过程称为外迭代。具体耦合流程示于图1。图1中，大方框外为输入参数，其中，下标i为区间号，k为i－1以下的区间号，j为燃料球种类号；A为矩阵；¯σi，j为对能谱和空间平均的单群截面；¯φi为能谱和空间平均的相对中子注量率；¯Φi为对应的实际中子注量率；Ti，j为区间i燃料球j的滞留时间；Ni，j（t）为新料Nj经i－1个区间辐照后在i区间t时刻的成分；¯Ni为各类型燃料平均核素密度之和；kn为第n次循环计算得到的keff；dev和σ为用户定义的收敛域。每次循环计算判断keff是否收敛在σ以内，不收敛则更新单群截面和单群中子注量率继续计算；收敛则进一步判断是否与预期值k0相差在dev以内，若在dev域值以外则修改添球速率继续计算，否则结束计算。

1.1 平衡态燃耗方程处理

与一般的燃耗方程不同，球床堆堆芯的燃耗方程［5］为：

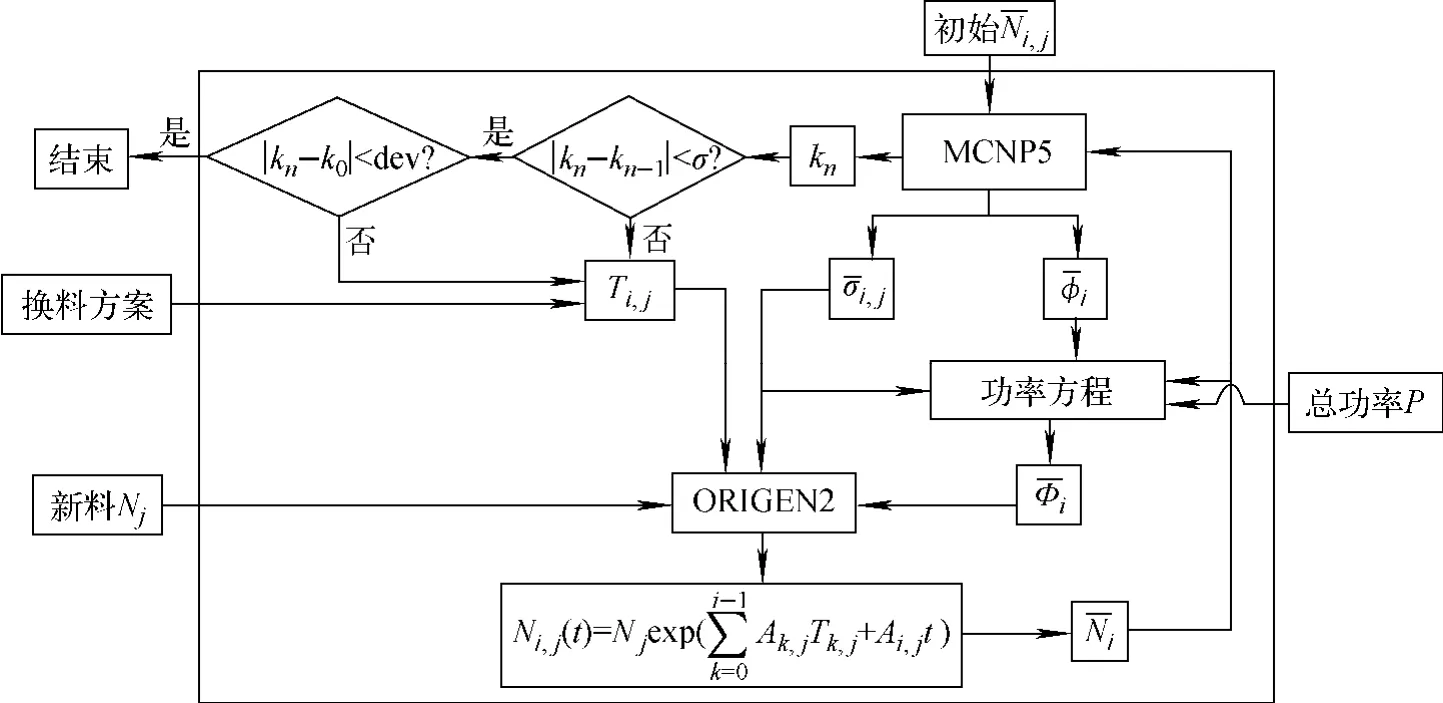
图1 燃耗耦合流程图Fig.1 Flow chart of coupled burnup code

其中：N（r，t）为堆芯r处t时刻的燃料核素成分组成的向量；v（r，t）为r处t时刻燃料的流动速度矢量，其值由换料方案决定；A（φ（r，t），σ（r，t），λ）为矩阵系数，矩阵元是r处t时刻的中子注量率、单群截面和衰变常量的函数。在平衡态时，忽略局部的随机扰动，假定堆芯各物理参数分布稳定，式（1）不含时间变量，可转化为：

式（2）中成分、中子注量率和单群截面与空间相关，使用MCNP5求解，必须对堆芯划分区间，中子注量率和单群截面为区间内的平均值，此即对空间项做离散化处理。为维持动态平衡，某区间内的核素随时间的演化与核素在空间上的泄漏等价，故式（2）可转化成：

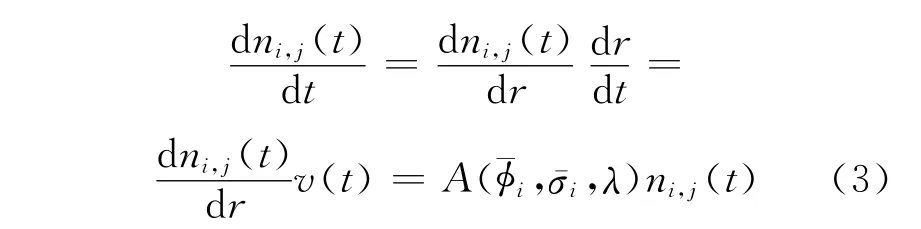
式中：ni，j（t）为区间i内滞留时刻t的第j种燃料球成分；¯φi和¯σi分别为区间i内的平均中子注量率和平均单群截面。区间滞留时间可通过流动速度和区间体积获得，此处假设所有球在该区间内具有相同的流动轨迹。式（3）可由ORIGEN2求解。至此，球床堆平衡态堆芯燃耗方程的求解，转化为对各分区各球在其滞留时间内的点燃耗计算。堆芯各区间成分由流经其内的各燃料球平均成分求和得到。

1.2 区域成分平均处理

结合式（3），区域内单个种类燃料球的平均成分为：

式中，Ti，j为区间i内的j类型燃料球的滞留时间。式中的Ai难以处理，将指数泰勒展开取二阶近似，结合式（3）简化为：

式中，ni，j（Ti，j＋Δt）和ni，j（Ti，j）可通过ORIGEN2求出。考虑到ORIGEN2给出的成分保留5位有效数字，Δt的选取不宜过小。

区域总的平均成分是流经该区的各类型燃料球平均成分之和。若区域内燃耗分布很大，得到的平均成分与实际成分对keff的影响可能不同，因此，要求堆芯区间划分得足够多。

1.3 MCNP5建模处理

MCNP5模型中燃料球并不流动，模型几何结构不更改，迭代中，只对燃耗的成分进行更新。焚烧的成分既可是燃料，也可是含硼的石墨。VSOP中某区域的成分是从上一区域转移下来的，因此，流道上的分段必须是等体积的，所有的区间必须是等流动时间间隔。而本方法中各区成分均从新燃料球沿流动轨迹依次解燃耗方程得到，空间和时间已合并，因此，对区间的划分无约束。为实现不同燃料类型、富集度、碳／重金属比（燃料装载量）的球的混合流动，需堆芯初始按一定比例混合建模，混合比例依赖于换料方案。

MCNP5建模可能带来的误差是，与实际的燃料间隔着石墨包壳不同，各区间的燃料可能在一个球内直接接触，产生额外的空间屏蔽效应，尤其是不同燃料类型之间。

1.4 换料方案处理

换料方案包括循环次数、循环流道、添球速率及堆外滞留时间等。为求解单个球的燃耗，需将换料方案转化成各新球从开始加入堆芯到最后卸出堆芯的整个流动轨迹。所以换料方案给定了区间燃耗计算的次序以及区间平均成分和平均燃耗深度的计算方法。文中换料方案的修改只针对添球速率，循环轨迹不变。PBRE可实现在同一流道内对不同燃料类型、富集度、燃料装载量的球分别计算，并能保存其几何上的异质性。

2 燃料球添球速率修改方法

本文提供线性关系和正相关两种方法修改燃料球的添球速率，计算模型则采用HTR-10堆芯。

2.1 线性关系法

添球速率V（kgU／d）与堆芯总功率P（MW）和堆芯平均卸料燃耗深度U（MW·d／kgU）的关系为：

平衡态时，不同堆芯平均卸料燃耗深度与keff在临界前后存在近似线性关系（图2）。因此，假定V与keff存在如下关系：

V＝B／（－keff＋A）（7）

式中，A和B为正数。A和B的数值由前两次迭代求出，过程如下。

图2 keff与平均卸料燃耗深度的关系Fig.2 keffvs average discharged burnup

第1次迭代：初装载计算认为V为无穷大，此时有：

第2次迭代：添球速率为猜测值V2，此时有：

第3次迭代：添球速率采用式（7）计算，其中，keff为预期设定的值。实际上，卸料燃耗深度与keff并非严格的线性关系，为能实现局部线性关系，A和B需不断更新，更新方法为：

式（10）取绝对值是为了避免统计扰动带来负值。

第n次迭代：当keff收敛在设定域值内时，不修改添球速率，因为此时受MCNP5统计扰动的影响大；若接下来的4次循环仍收敛，则完成计算并结束任务，否则修改添球速率继续计算。

由于MCNP5存在统计误差，因此收敛域不能较统计误差小。

图3示出了迭代收敛的结果，两条虚线之间为1次外迭代，虚线之间的数据点为该外迭代下的内迭代点。为分析初始设定添球速率对迭代次数的影响，分别计算单个通道初始新球添球速率为100、28.37、20、15g（UO2）／d的收敛情况。从图3可知：不同初始添球速率均可在2～3个外迭代内实现收敛，初始添球速率越接近收敛值（28g（UO2）／d附近），收敛越快；初始添球速率越大，第1次内迭代数越少，情况a和b分别用了4次，情况c用了6次，情况d用了10次；情况a、b、c、d下达到收敛时，MCNP5总的计算次数分别为15、11、13、20，收敛时间不一致。结果表明，线性关系法在收敛计算上相当有效，但计算时间与初始添球速率有关，需根据预期燃耗深度推测初始添球速率。

图3 线性关系法不同初始添球速率下的keff迭代收敛Fig.3 Convergence of keffwith linear relation method in different initial feedrates

为减少MCNP5的计算次数，将线性关系法的内外迭代合并，计算结果示于图4。情况d的震荡很明显，收敛很慢，情况a开始时在收敛域徘徊，20个迭代后发散。原因是内迭代不稳定的情况下，新燃料球的添球速率与keff的关系式（式（7））完全破坏，修正不具可靠性。

2.2 正相关法

内外迭代合并的情况下，为保障迭代的收敛性，必须维持keff与添球速率的正相关性。给出一简单的关系式：

式（11）虽收敛稳定，但收敛速度很慢。为加速收敛，必须考虑添球速率变化幅度与keff变化幅度的关系。对式（7）两边微分，有：

图4 内外迭代合并下keff和添球速率的收敛Fig.4 Convergence of keffand feedrate in merged iteration process

A等于keff1，选取修正幅度为预期值keff0附近的幅度，则添球速率可修改为：

式（13）确保了V的数值为正，同时也考虑了初始装载不同的影响。

采用正相关法计算得到的结果示于图5，图5中增加了初始添球速率1 000g（UO2）／d的情况（情况e）。keff在10个迭代步内基本收敛，相比线性关系法，减少了一定的计算时间，同时对不同的添球速率不敏感，可靠性较高。

图5 正相关法下的keff迭代收敛Fig.5 Convergence of keffwith positive correction method

3 HTR-10验算

3.1 模型及区域划分

采用清华大学HTR-10作为PBRE程序的验算基准题。堆芯模型示于图6，具体模型参数见文献［6］。每个新燃料球含5g铀，235U富集度为18%，活性区球填充因子为60%，所有材料均计入硼当量。受MCNP5允许的最大存储空间限制，本文不对堆芯进行温度分区，根据文献［7］提供的温度分布图，将温度进行平均近似处理，选取堆芯燃料温度为880K，堆芯石墨温度设定为860K，周围反射层石墨取中间位置的温度，设为800K。堆芯顶空腔高41.3cm，平衡态时，堆芯装载2.7万个燃料球，计算中卸料管内无燃料球。堆芯活性区径向根据文献［8］提供的7∶10∶12∶16∶21体积比例划分，但划分曲线与实际流道曲线不同。轴向等高度将每个流道分成7个区，堆芯共划分成35个区。燃料球的流动方式采用5次通过堆芯的方案［8－10］。

图6 HTR-10建模纵、横剖面Fig.6 Vertical and horizontal cross sections of HTR-10modeling

3.2 计算结果分析

控制棒全抽出，平衡态时keff为1.01左右［8］。设定每个流道的新燃料球添球速率为28.37g（UO2）／d，此时卸料平均燃耗深度为80MW·d／kgU，计算得到keff收敛为1.007。设定预期keff为1.01，收敛域为0.001，则计算得到每流道新燃料球添球速率为28.8g（UO2）／d，此时平均卸料燃耗深度为78.9MW·d／kgU。

表1列出了燃耗深度的分布（径向区域标号从小到大表示从内到外，轴向区域标号从小到大表示从上到下），从径向上看，外道燃耗深度较内道的大，主要因为外道滞留时间长；轴向上因为采用5次通过的方式，所以燃耗深度分布差别不大；堆芯整体平均燃耗深度为43.16MW· d／kgU。因为轴向划分与VSOP并不相同，堆芯燃耗分布无法与文献结果比较，但各流道的卸料燃耗深度与文献［9］的值仅相差2MW· d／kgU，分布较为一致。

表1 堆芯各区燃耗深度分布Table 1 Burnup distribution of core

表2所列为各区域中子注量率分布，最高注量率位于堆芯中央，约1.0×1014cm－2· s－1。中子注量率径向分布较平坦；在轴向上则因为泄漏的原因，中子注量率差异略大。

表2 堆芯各区中子注量率分布Table 2 Fluence rate distribution of core

表3列出了堆芯功率密度分布，最大功率密度为2.46MW／m3，堆芯平均功率密度为2MW／m3，功率峰因子很小，仅1.23，较文献［9］的小8%，可能是堆芯分区少的缘故。与中子注量率和燃耗深度在径向分布不同的是，功率密度在径向上并非单调减少，而是在外流道略微增大，尤其是堆芯锥体卸出口的规律与之完全相反。因为HTR-10堆芯小，中子泄漏大，外流道受石墨反射层的影响大，能谱更软，所以其裂变截面相对增大，导致功率密度增大。235U的单群裂变截面分布列于表4，整个分布呈堆芯中间小、外围大的规律，与中子注量率相反。

表3 堆芯各区功率密度分布Table 3 Power density distribution of core

表4 堆芯各区235U单群裂变截面分布Table 4 One-group fission cross section distribution of235U in core

4 小结

本文针对球床高温堆流动特性导致的燃耗分析难点，采用MCNP5和ORIGEN2耦合的方法，开发了1套平衡态球床高温堆的燃耗分析程序PBRE，并采用该程序对HTR-10堆芯进行了模拟，计算了燃耗深度、中子注量率、功率分布等数据。分析表明，keff＝1.01时，堆芯平均卸料燃耗以及各流道卸料燃耗深度分布与文献值基本吻合。同时，经实测，通过对迭代收敛的加速分析，有效地减少了计算时间，MCNP5需约10次计算即可得到平衡态参数。因此，基本验证了PBRE程序的可靠性，可将该程序用于球床堆平衡态堆芯的相关分析计算。堆芯温度分布的获取、燃耗计算的温度分区以及结合流动规律程序更好地给出换料方案，则将是PBRE下一步的研究内容。

［1］ RÜTTEN H J，HAAS K A，BROCKMAN H，et al.VSOP（99／05）computer code system［M］.Zentralbibliothek：Forschungszentrum Jülich GmbH，2005.

［2］ SEKIMOTO H，OBARA T，YUKINORI S，et al.New method to analyze equilibrium cycle of pebble-bed reactors［J］.Journal of Nuclear Science and Technology，1987，24（10）：765-772.

［3］ GOUGAR H D.Advanced core design and fuel management for pebble-bed reactors［D］.US：The Pennsylvania State University，2004.

［4］ FRATONI M.Development and applications of methodologies for the neutronic design of the Pebble Bed Advanced High Temperature Reactor（PB-AHTR）［D］.Berkeley，US：University of California，2008.

［5］ MASSIMO L.Physics of high-temperature reactors［M］.Holland：Elsevier，1976.

［6］ 经荥清，杨永伟，许云林.蒙特卡罗方法用于HTR-10首次临界燃料装料预估的校算［J］.核动力工程，2005，26（1）：28-34.

JING Xingqing，YANG Yongwei，XU Yunlin.Application of Monte Carlo method for verification calculation in fuel loading prediction for first criticality of HTR-10［J］.Nuclear Power Engineering，2005，26（1）：28-34（in Chinese）.

［7］ GAO Z，SHI L.Thermal hydraulic calculation of the HTR-10for the initial and equilibrium core［J］.Nuclear Engineering and Design，2002，218（1）：51-64.

［8］ 吴宗鑫，经荥清.HRT-10的燃料管理［J］.清华大学学报：自然科学版，2001，41（4）：120-123.

WU Zongxin，JING Xingqing.Fuel management of HTR-10［J］.J Tsinghua Univ：Sci ＆Tech，2001，41（4）：120-123（in Chinese）.

［9］ 经荥清，张旭，罗经宇.HTR-10MW高温气冷实验堆换料方式的研究［J］.核科学与工程，1993，13（2）：119-125.

JING Xingqing，ZHANG Xu，LUO Jingyu.The study on the shuffling scheme in HTR-10MW test module［J］.Chinese Journal of Nuclear Science and Engineering，1993，13（2）：119-125（in Chinese）.

［10］杨永伟，经荥清，许云林，等.HTR-10平衡态运行方式研究［J］.清华大学学报：自然科学版，1995，35（6）：12-16.

YANG Yongwei，JING Xingqing，XU Yunlin，et al.Study of operation model at equilibrium state of core for HTR-10［J］.J Tsinghua Univ：Sci ＆Tech，1995，35（6）：12-16（in Chinese）.

Development of Burnup Calculation Code for Pebble-bed High Temperature Reactor at Equilibrium State

ZHU Gui-feng1，2，3，ZOU Yang1，2，LI Ming-hai1，2，YAN Rui1，2，
PENG Hong-hua1，2，XU Hong－jie1，2，＊
（1.Shanghai Institute of Applied Physics，Chinese Academy of Sciences，Shanghai 201800，China；2.Key Laboratory of Nuclear Radiation and Nuclear Energy Technology，Chinese Academy of Sciences，Shanghai 201800，China；3.University of Chinese Academy of Sciences，Beijing100049，China）

The burnup calculation code PBRE coupling MCNP5and ORIGEN2was developed for pebble-bed high temperature reactor at equilibrium state，and it can be used to analyze the neutronic performance of equilibrium core.The iteration method was optimized in order to save Monte Carlo calculation time，and the convergence can be reached in 10iterative steps.The average discharged burnup for HTR-10is consistent with literature，and it indicates that the PBRE is suitable to analyze the burnup for pebble-bed reactor at equilibrium state.

PBR；equilibrium state；burnup；PBRE

TL32

：A

：1000-6931（2015）05-0890-07

10.7538／yzk.2015.49.05.0890

2014-01-22；

2014-04-22

中国科学院战略性先导科技专项资助项目（XDA02010200）；上海市科技创新重点项目资助（11JC1414900）；国家自然科学基金青年基金资助项目（11005148）；973计划资助项目（2010CB934501）

朱贵凤（1987—），男，江西九江人，博士研究生，核科学与工程专业

＊通信作者：徐洪杰，E-mail：xuhongjie＠sinap.ac.cn