PWM整流器EL模型无源性控制策略

宋平岗 马卫东 李云丰

（华东交通大学电气与电子工程学院，南昌 330013）

传统不可控二极管整流器[1]和采用晶闸管的整流器[2-3]即使在理想电网电压情况下也会造成电网污染严重，尽管使用了12 脉波甚至更高脉波都无法有效地控制直流电压跟踪参考给定值，当电网电压闪变以及负载突变的情况下更为严重[4]。传统整流器采用的是相控的方式，整流器本身需要消耗大量无功，谐波成分复杂，同时还需要体积笨重而庞大的滤波装置以及无功补偿装 置，增加了设备的运行与维修费用以及设备的占地面积[5]。基于全控器件电压源型PWM（Pulse Width Modulation）整流器很好的解决了上述问题，具有功率因数高、直流电压可控性强、抗负载变化能力强、无需无功补偿等优点[6]。

PWM 整流器的控制策略从以往的间接电流控制发展到直接电流控制[5]，其中直接电流控制中从环策略逐步发展到直接功率控制[7]、反馈线性化控制和滑膜控制[8]以及无源性控制[9-10]等。以往基于欧拉-拉格朗日（Euler-Lagrange，EL）模型[10]的无源性控制策略没有讨论系统参数变化对控制性能的影响。本文从PWM 整流器在同步dq 旋转坐标系出发，建立了直接电流下的EL 模型，并设计了相应的无源控制器，指出在整流器等效阻感发生变化的时候直流侧输出电压达到实际要求，考虑直流电压的变化与交流电流的有功分量的变化呈现正相关，因此本文提出利用微调调节器对有功分量进行补偿，即将直流电压反馈值控制系统利用比例积分（Proportional Integral，PI）控制器进行补偿。

1 PWM 整流器基本原理

图1所示为采用电压源型PWM 整流器的基本结构图[5]，图中usa、usb、usc和isa、isb、isc分别为三相电压和三相电流，uca、ucb、ucc为整流器交流侧输出电压，R0和L0分别为等效电阻和电感，T1—T6 和D1—D6分别为功率开关管和续流二极管，idc为整流器直流侧输出电流，C为支撑电容值，udc为直流侧电压，ic为电容电流，iR为流过等效电阻RL的电流。

图1 PWM 整流器基本结构

定义Sj=1 表示j（j=a、b、c）相上功率管开通下功率管关断，Sj=0 表示j相上功率管关断下功率管开通。根据基尔霍夫电压和电流定律可得PWM整流器在三相静止坐标系上的方程为

忽略udc的波动，利用同步dq 坐标变换将式（1）、式（2）变换至dq 坐标系中可得

式中，usd、usq和isd，isq分别为三相电压和电流在d轴和q 轴上的分量，其中usd=Um，usq=0，Um为相电压幅值；Sd和Sq分别为开关函数在d 轴和q 轴上的分量，ω为系统角频率。

2 PWM 整流器无源模型和无源控制器设计

2.1 PWM 整流器EL 模型

将式（3）进行整合写成动态矩阵相乘的形式，得到PWM 整流器基于EL 模型[10]为

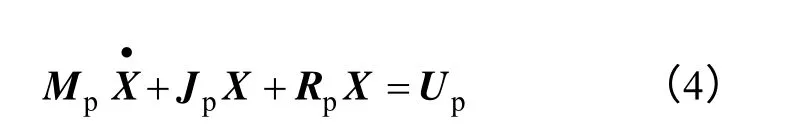
式（4）中X=[isdisqudc]T；Mp=diag([L0L02C/3])；Jp=[0 -ωL0Sd; ωL00Sq;-Sd-Sq0]反映了PWM 整流器系统内部的互联结构；Rp=diag([R0R02RL/3])反映了PWM 整流器系统的耗散特性，Up=[Um0 0]T表征PWM 整流器系统内部和外部的能量交换矩阵。

2.2 PWM 整流器无源控制器设计

基于EL 模型的PWM 整流器无源控制器是采用某种控制规律[9]，尽快的将整流器实际输出快速稳定的跟踪期望输出，即通过控制整流器实际输出与给定输出误差为零使得整流器实现控制系统下达的命令。令Xdes表示系统状态向量X的期望输出值（以下中凡是上标有“*”号都表示相应量的参考值，下文不再一一介绍），Xreal则表示X实际输出值，那么系统误差量为Xerr=Xreal-X*des。选取能量误差函数为李雅普若夫函数

能量误差函数的衰减速度与系统等效衰减时间常数有很大的关系，即衰减时间常数越小，能量衰减越快，跟随速度越快，那么可以采用阻尼注入法减小误差衰减时间常数，即构造一个额外能量耗散矩阵增加衰减速度，因此增加耗散项Ra=diag([Ra1Ra2Ra3])。需要说明的是采用增加阻尼方法[10]只是会加快能量误差衰减的速度，但是不能真正意义上完全稳定的消除误差，本文将在后文增加微调PI 调节器实现整流器输出电压快速跟踪参考给定值。将Xerr=Xreal-X*des代入式（4）并在式（4）两边同时加上RaXerr，可得

选取如式（7）所示的控制规律

式（8）表明，只要选取的耗散矩阵元素值大于零，即可使式（8）在大范围内渐进稳定。将式（7）代入式（4）中，解方程得到整流器交流侧电压在d轴和q 轴上的参考分量为

将式（8）代入式（3）中，得到

式中，一般选取Ra1=Ra2，Ra1一定大后，isd和isq能 快速跟踪参考值is*d和is*q，那么可认为isd=is*d，即式 （10）中功率方程可以化简为

式（11）为PWM 整流器系统的能量平衡方程，有功电流参考分量可以从式（11）的稳态中求得（舍去另一不符合实际根），即

式中，Idc为idc的平均值，从此式可以看出，有功参 考分量is*d对系统参数较为敏感，PWM 整流器交流侧等效电阻R0的变化将会导致is*d的变化，根据 式（3）第三式可知，直流侧电压将会发生变化，导致控制系统不稳定。为了消除此影响，利用微调PI 调节器产生有功补偿分量，即is*d最后的表达式为

式中，Δisd=(Udc-udc)(kp+ki/s)，其中Udc为直流电压参考值，kp，ki为比例和积分系数。一般情况下PWM整流器工作在单位功率因数，因此无功功率参考值 为零，那么is*q=0。

3 仿真分析

为验证所设计控制器的正确性， 在Matlab/Simulink 中搭建了上述的仿真模型，研究整流器在负载突变和直流参考电压突变时的动稳态特性，仿真基本参数为：线电压有效值Us=380V、直流电压Udc=800V、电容值C=1mF、等效电阻R0=0.5 Ω，等效电感L0=5mH。仿真设置在0.1s时直流电压参考值由800V 跳变至850V，0.15s时跳回800V，负载电阻RL在0.2s 前一直为20 Ω，在0.2s时并入一个50 Ω的电阻。为验证所设计控制器的有效性，控制系统中令等效电阻R0=0.48 Ω，与主电阻相差0.02Ω。分别仿真没有微调补偿和有微调补偿两种策略，对比两者的效果，如图2所示。

图2 仿真波形

图2（a）为有补偿（改进方法）和没有补偿时的直流电压波形，从图中可以明显的看出来，补偿后直流电压能稳定的控制在给定值左右，并且抗负载变化能力也非常强，动态响应快，但是未补偿不仅动态响应慢，而且还不能控制在给定值左右。图2（b）为补偿后电网三相交流电流，波形对称，畸变率很小。图2（c）则是补偿后电网发出的有功功率和无功功率，很明显，不管有功功率怎样变化，无功功率都能维持在零左右，实现了PWM 整流器的单位功率因数控制。

4 结论

本文从PWM 整流器电磁暂态数学模型角度出发，建立了改进型的基于EL 模型的无源控制器，将整流器直流侧电压反馈值控制系统与给定值比较后经PI 调节器产生补偿分量，用于消除因系统参数变化产生的不良影响，并通过仿真结果验证了本文所设计控制系统的正确性。

[1] 潘启军,刘德志. 变抽头六相整流电路的分析[J]. 中国电机工程学报,2003,23(12): 146-152.

[2] 卓放,裴云庆,周新,等. 有源电力滤波器在抑制晶闸管相控整流电源谐波方面的应用[J]. 电网技术,2004,28(2): 40-42.

[3] 叶凯,于贵,张青庆. 晶闸管弧焊整流数字控制[J]. 电焊机,2013,43(4).

[4] 陈明,徐伟,姚正武. 三相整流设备晶闸管选用研究及功率因数分析[J]. 电气工程应用,2013 (1): 23-26.

[5] 陈诚， 王勋， 程宏波. 三相PWM 整流系统的研究[J]. 华东交通大学学报,2012,29(6): 40-44.

[6] 张笑微,李永东,刘军. PWM 整流器电流控制策略的研究[J]. 电工技术杂志,2003(12): 57-59.

[7] 陈伟,邹旭东,唐健,等. 三相电压型PWM 整流器直接功率控制调制机制[J]. 中国电机工程学报,2010 (3): 35-41.

[8] 张志,谢运祥,乐江源,等. 三相电压型PWM 整流器的反馈线性化和滑模控制[J]. 华南理工大学学报(自然科学版),2009,37(11): 71-75.

[9] 王久和,张巧杰,王勉. 三相四线电压型PWM 整流器混合无源控制[J]. 电工技术学报,2013,28(7): 212-217.

[10] 王久和,黄立培,杨秀媛. 三相电压型PWM 整流器的无源性功率控制[J]. 中国电机工程学报,2008,28(21): 20-25.