HTR-PM反应堆保护系统软件可靠性模型的初步研究

崔聪，李铎，郭超

（清华大学核能与新能源技术研究院，先进核能技术协同创新中心，先进反应堆工程与安全教育部重点实验室，北京 100084）

华能山东石岛湾核电站高温气冷堆电站示范工程（以下简称HTR-PM）是国家“十一五”重大专项支持的重点工程， HTR-PM数字化保护系统是高温气冷堆核电站重大专项关键技术及相关试验研究项目之一，是专门针对HTRPM的保护功能和性能要求开发的专用系统，针对性强，结构简单[1]。

为了提高HTR-PM的安全性，就要提高保护系统软件的质量，而衡量软件质量的最重要指标的之一就是可靠性。因此，要研究HTR-PM保护系统的软件可靠性具有重要意义。

软件可靠性，即软件系统在一定时间内不发生故障的概率[2]。研究软件可靠性问题的有效手段之一就是根据过去的失效数据进行建模，以预测未来数据的变化趋势。该方法使用与时间相关的失效数据，由于随着测试时间的推进，软件可靠性逐渐提高，所以使用这种手段建立的模型又叫做软件可靠性增长模型（SRGM）。在此基础上开发出的非齐次泊松过程（NHPP）故障分类软件可靠性模型应用广泛，NHPP模型的主要问题是在不同的假设条件下确定合适的期望累计故障数函数，所以，本文研究的主要内容分两方面：

1）对已有与软件故障分类相关的非齐次泊松过程（NHPP）模型归纳整理，分解模型结构，把假设条件统一处理，从处理手段、数学公式、软件工程意义角度整理归纳。

2）在已有错误严重程度的模型基础上，利用关键错误占错误总数的变化趋势曲线进行建模研究并分析结果。

1 与软件故障分类相关的NHPP模型综述

非其次泊松过程（NHPP）模型在软件可靠性增长模型占有绝对的优势，本文重点研究和总结了与软件故障分类相关的NHPP模型，并在此基础上提出了基于软件故障分类的新的软件可靠性模型。

1.1 具有时延的故障分类模型

在 GO模型之后，由于在实际情况中相对于假设的指数增长模型，S型软件可靠性增长更经常的观测到，所以M.Ohba和S.Yamada提出了S型模型，即考虑了故障检测或移除的延时问题[3]。1984年M.Ohaba对指数模型、DSS型和ISS型模型进行了总结[4]。而后Shigeru Yamada提出了故障分类模型[5]，故障按照检测难易度进行分类，但是故障检测率都是常数，故障类型只是通过检测率的大小来区分。Mitsuhiro Kimura和Shigeru Yamada对故障分类进行了细化，首次提出了根据延时的程度来区分故障类型[6]，但是在他们的模型中只考虑了两种故障。后来又开发出3故障类型模型[7]，第一种故障类型假设故障检测率为常数即S型，第二种假设为DSS型，第3种假设为Erlang型。2008年，Omar Shatnawi和P.K.Kaupur提出了一种广义的故障分类模型[8]，作者首先研究了软件系统中存在的最容易分析的简单、困难、复杂3种故障的情况，然后把复杂故障推广到要经过N步才能移除的故障类型，而这种故障分类涵盖了DSS型、ISS型和广义的Erlang型模型，该模型结构如下：

1）基本假设

A2.每个故障的严重性和被检测到的可能性大致相同；A3.在任何时间间隔内检测到的故障数是相互独立的；A4.故障分类—按照故障移除的难易度2）基本公式

不同故障类型需要阶段不同，简单故障一个阶段立即移除，困难故障需要两个阶段才能移除，复杂故障需经过检测过程、分析过程和移除过程三个阶段，同时考虑学习因素，推广到n个阶段，则有：

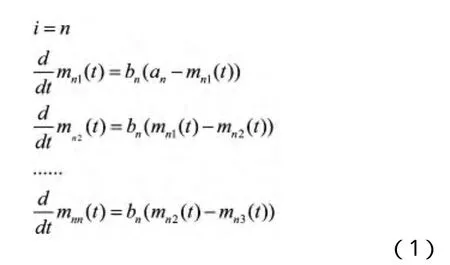
1.2 不完美除错的故障分类模型

不完美除错，即考虑错误移除的不彻底和移错过程中引入新错误。Tom Lynch和Hoang Pham首次提出了将故障分类和不完美除错中的引入新错误放在一起考虑[9]，其中故障分类还是按照不同的检测率常数 来区分故障类型。后来，P.K.Kapur和Sunil Kumar Khatri对这一模型进行了完善，同时考虑不完美除错的移除成功率和引错概率，并且在区分故障类型上也采用了时延的方法[10]，该模型如下：

1）假设条件

A1、A2、A3同上；A4.故障分类—按照故障移除难易度A5.不完美除错—引入错误和移错延时

2）基本公式

简单故障，一步就可以移除，困难故障需要两个过程—观察和移除才能彻底将故障移除，但是由于要考虑除错的不彻底和引入错误，所以需要将观察和移除的两步式子合为一个式子，有：

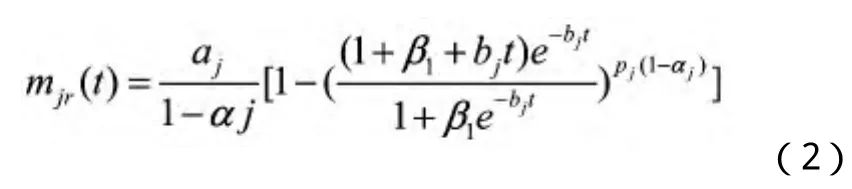
同理，复杂故障：

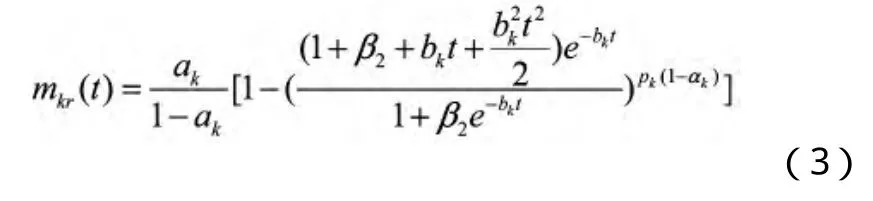
1.3 对故障检测率分解处理的模型

在硬件系统中故障检测率经常是递增或者递减，递减是由于修复设计相关的应将故障，递增是由于硬件组件的老化磨损[11]。如果不考虑引入错误，软件系统通常是有一个递减的故障率，因为软件不会老化磨损。然而软件故障检测率还要考虑它的测试措施，不同的测试措施导致了不同的故障检测率，例如，考虑Weibull-type和Logistic类型的测试函数[12-13]。Sy-Yen和Yu Huang提出了将 分解为测试函数和FDR的乘积[14]，拓展了 的含义。

1)假设条件

A1、A2、A3同上；A4.对 进行分解处理

2）基本公式

式中，函数为可评估的测试过程（TE）包括人力、测试案例和CPU时间等，而测试过程说明了软件故障被检测的效率，TE的表达式 可以为常数、威布尔分布和Logistic函数。函数为FDR严重依赖于测试的技术、程序的大小和软件的测试能力，有3种随时间的变化：增长、减少、恒定不变。由此得到可以为常数、非增函数和非减函数。这里拓展了意义，把测试过程和故障检测率同时考虑。选择合适的代入到式（4）中即可解得

1.4 变点和故障分类模型

很多SGRM模型假设故障检测率是常数，故障在整个时间段上的分布是相同的，不随时间改变。但是实际情况是，故障的分布受到很多因素影响，例如运行环境、测试策略以及资源分配。一旦这些条件发生改变，就可能导致软件故障密度函数非单调的变化，这个问题称作变点问题。不同时间段上故障检测率可以为不同的值，而这些时间段之间的时间节点就叫做变点。变点问题最早由Zhao.M.提出[15]。后来Huan-Jyh Shyur提出了将变点问题和不完美除错结合考虑建立模型，故障检测率和故障引入率一起随时间区间段变化[16]。2007年P.K.Kapur等人提出了将变点和不同故障种类相结合建立模型，其中故障检测率根据时间区间和故障种类不同而取不同值[17]。同年，D.N.Goswami等人扩大了故障检测率的取值范围[18]，该模型如下：

1）假设条件

A1、A2、A3同上；A4.变点；A5.故障分类—故障的严重程度。

2）基本公式

通过变点把测试过程分为不同区间，并且在同一区间上，不同类型的故障的检测率也是不同，考虑测试经验的获得，对于简单故障由于其最容易被检测到，所以移除率值最大。而对于困难和复杂故障，由于难以检测，并且检测后还要进行分析原因，所以在测试过程结束时FFR可能减少。

1.5 与故障数分布函数F(t)相关的可靠性模型

出于经济和软件工程考虑，大多数软件的发布都不是最终和完美版本，软件更新是一个复杂的过程，上一个版本的部分软件错误往往会留到下一个软件版本中并对下一个版本产生影响，据此Amir.H.S.Garmabaki和Anu.G.Aggarwal提出的软件更新换代的模型[19]。

1）假设条件

A1、A2、A3同上；A4.故障分类—按照故障移除的难易度；A5.版本更新2）基本公式

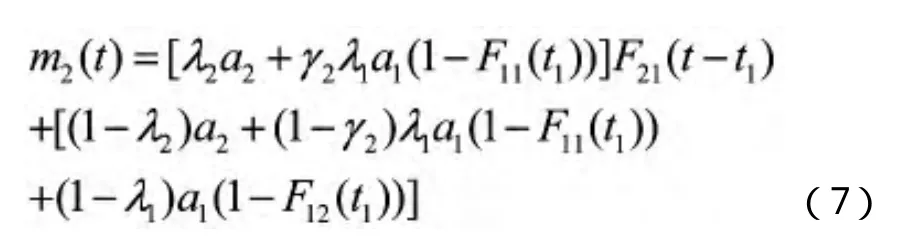
Kuei-Chen Chiu曾经提出一种表现与发现错误有关的自动错误检测因素 、学习因素 和忽略因素 的模型[20]。其中，故障分布的密度函数为。后来，Javaid Iabal和N.Ahmad对这个模型进行了改进，把学习因素分为了自主学习因素和获得性学习因素，使得更加符合实际情况[21]。

a）假设条件

A1、A2、A3同上；A4.考虑学习因素、自动检测因素、忽略因素

b）基本公式

自主学习和自动错误检测过程有关，而获得性学习和经验的故障检测有关，所以有如下式子

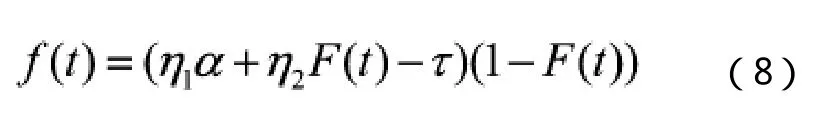
1.6 NHPP模型总结

根据对上述五大类模型的所有假设条件为：A1，A2，A3；A4.故障分类—按照故障移除的难易度、故障检测难易度、故障严重程度；A5.不完美除错—包括除错不完全和引入新错误；A6.根据工程意义对 进行分解；A7.变点；A8.版本更新；A9.对于分布函数 的处理。

2 对故障之间关系的建模

从第一章已有的5大类模型看出现有模型大多只是单纯的进行故障分类，并对不同种类的故障之间的发展趋势进行研究。不同种类的故障具有不同的发展趋势，即每一类故障在总体故障中的占比是发展、变化的，充分利用这些信息研究故障的变化趋势可从另一方面入手研究软件可靠性模型。在文献[22]中作者错误比重函数采用Logistic函数来描述取得较好结果，本文在此模型基础上对关键错误占错误总数变化趋势曲线进行了建模研究，通过分析结果说明了研究故障间关系的适用性和必要性。

表1 的各种处理方式Table 1 All kinds of treatment

表1 的各种处理方式Table 1 All kinds of treatment

?

表2 的各种处理方式Table 2 A ll kinds of treatment

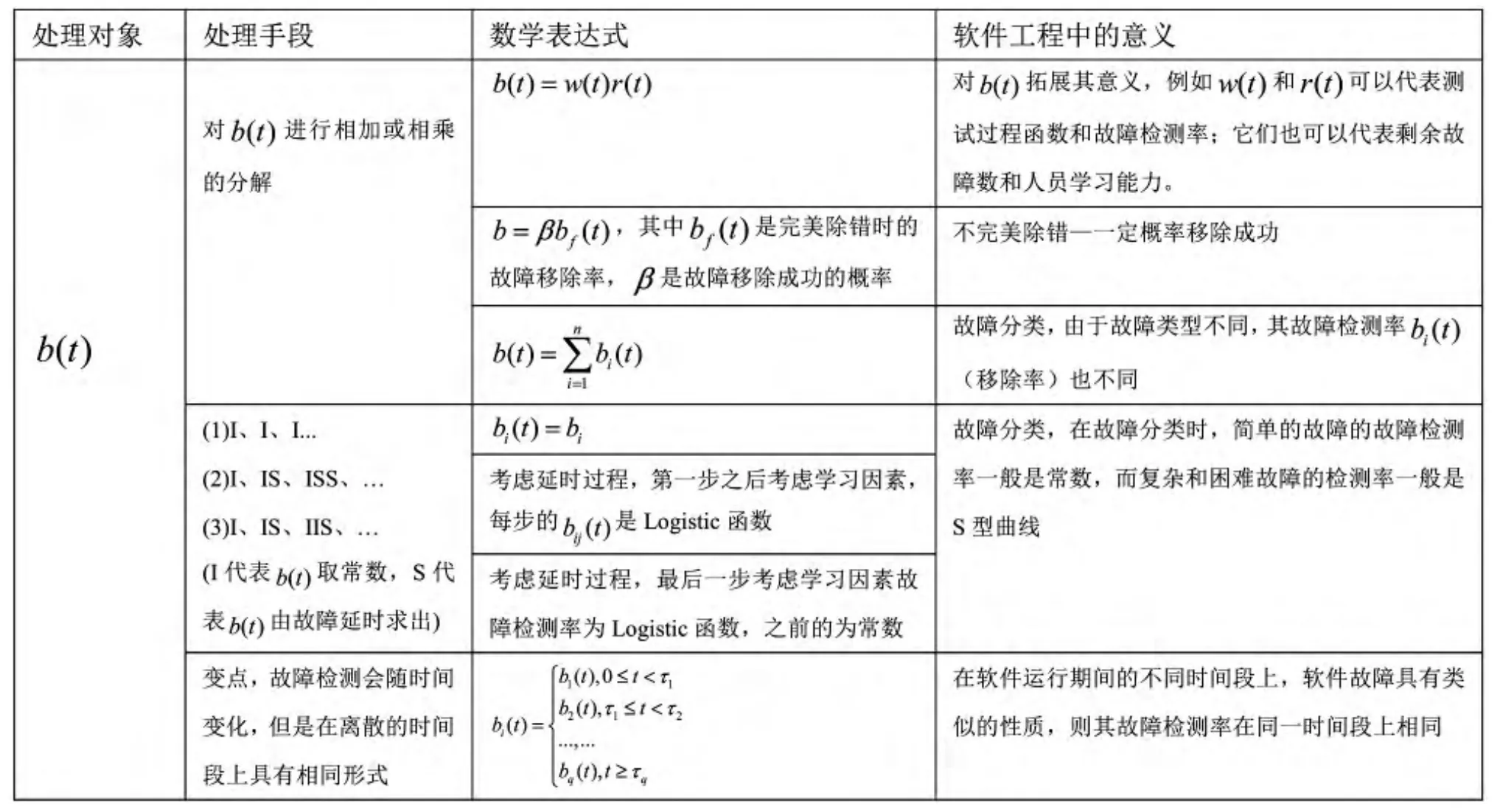
表2 的各种处理方式Table 2 A ll kinds of treatment

?

表3 的各种处理方式Table 3 All kinds of treatment

表3 的各种处理方式Table 3 All kinds of treatment

?

2.1 HTR-PM保护系统软件开发中的数据

本文使用HTR-PM保护系统开发过程的26个软件模块中的FirmSys_MCS_GPU100模块第一期的故障数据建模，并采用前40天的数据用来估计参数，而后80天的数据用来预测模型估计的准确性。表4是该模块120天内收集到的故障数据。

表4 检测过程不同严重程度错误数据Table 4 The detection process of severity error data

2.2 改进模型的步骤

（1）将关键错误比例数据点拟合为一条指数曲线。（2）利用拟合曲线推导出期望故障数的函数。

（3）故障数据点进行拟合求出待估参数以及平均方差MSE。

2.3 公式推导

根据文献[3]中，关键故障数比例呈指数形状，故假其比例k设为：

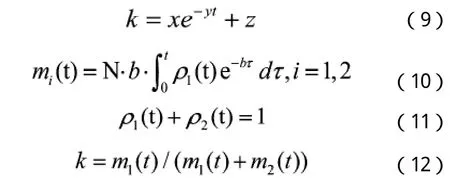
由(1)~(5)解得：

2.4 实例分析

2.4.1 使用MatLab进行比例函数的拟合

表5 比例函数的参数拟合结果Table 5 Proportion of function parameter fitting

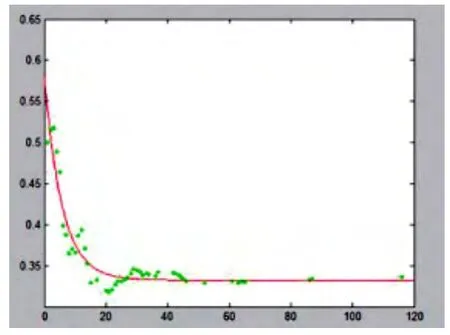
图1 关键错误占比数据和拟合结果Fig.1 Prcentage of critical errors and data fitting

图2的拟合曲线和实际累计故障数数据Fig.2 The fitted curve and the actual cumulative number of fault data

表6 参数估计结果Table 6 Parameter estimation

表6 参数估计结果Table 6 Parameter estimation

参数 N b本文的估计结果 353.761 0.0579

2.4.3 误差分析

表7 参数估计结果Table 7 Parameter estimation

从结果看出在数据拟合阶段，由于预先对参数进行了拟合，所以要比一步的参数估计误差要大一些，但是在可以接受的范围内；而数据预测效果则变的更好，也同样是因为考虑了严重程度故障比例的数据图，才使得预测误差变小。这样做的好处是，使错误严重比重的分类方法可以应用到更广的范围；又使得最后在进行参数估计（MLE和LSE）时减少了待求参数的个数，减少了计算量。

3 总结和展望

本文先对近30年来开发的各种类型的NHPP模型按照具有时延、不完美除错、对的分解、变点和这5个方面进行了分类研究，现有模型对故障间关系研究较少，于是在已有模型的基础上利用关键错误比重趋势曲线进行建模，得到了较好的估计结果，说明了研究故障间关系的必要性。

NHPP模型发展至今已有数十种，这里只选取了其中最主要的几类进行了整理研究，所以在未来的工作中可以吸收更多新类型NHPP模型以完善基本元素处理方式表；同时，现有软件可靠性模型都是具体问题具体分析，缺乏一种通用的模型，所以可以在处理方式表的基础上，从数学的角度将所有元素的特性整合为一个适用于大多数场合通用的模型，这样做可以节省重复建模的成本。另外，这里对于故障间关系的研究还只是一个开端，故障关系的特性往往能从一个新的角度反映故障累计数的变化趋势，因为它除了能反映故障本身变化特性，还能反映不同种类故障间的关系，例如可以根据故障关系曲线研究测试停止时间以及总故障数的变化趋势，而这些工作都需要在未来完成。

[1]李铎,等.HTR-PM反应堆保护系统工程样机的研制[J].仪器仪表用户,2013,20(5):36-38.

[2]Michael R.Lyu, etal.Handbook of Software Reliability Engineering.IEEE Computer Society Press and McGraw-H ill Book Company

[3]M.Ohba, S.Yamada, etal.S-shaped software reliability grow th curve: How good is it?.Proceedings IEEE COMPSAC 82,Chicago, 1982:38-44.

[4]M itsuru Ohba.Software reliability analysis models.IBM Journal of Research and Development, 1984, 28(4): 428-443.

[5]Shigeru Yamada, et al.A software reliability grow th model w ith two types of errors[J].EDP Sciences, 1985, 19(1): 87-104.

[6]M istuhiro Kim ura, et al.Softw are reliability assessment for an exponential-S-shaped reliability grow th phenomenon[J].Computer Math.Applic.1992, 24(1/2): 71-78.

[7]Kapur P.K., etal.Contributions to harew are and softw are reliability.World Scientific Publishing Co.Ltd.1999.

[8]Omar Shatnawi, et al.A Generalized Software Fault Classification Model[J].WSEAS Transactions on Computer, 2008.

[9]Tom Lynch, etal.Modeling software-reliability w ith multiple failure-types and imperfect debugging[A].Proceedings Annual Reliability and Maintainability Symposium[C].IEEE, 1994: 235-240.

[10]PKKapur, et al.Incorporating concept of two types of imperfect debugging for developing flexible software reliability grow th model in distributed development environment[J].Journal of Technology and Engineering Sciences, 2009, 1(1).

[11]S.Yamada, et al.Software reliability grow th model with Weibull testing effort: A model and application.IEEE Transactions on Reliabiliy, 1993, 42(1): 100-106.

[12]S.Yamada, et al.A TE dependent software reliability model and its application.Microelectronics and Reliability.1987.

[13]C.Y.Huang, et al.Analysis of a software reliability grow th model w ith logistic TE function[A].Software Reliability Engineering,1997.Proceedings., The Eighth International Symposium on[C].1997:378-388.

[14]Sy-Yen Kuo, et al.Framework for modeling software reliability,using various testing-efforts and fault-detection rates[J].IEEE Transactions on reliability, 2001, 50(3):310-320.

[15]Ming Zhao.Change-point problems in software and hardware reliability.Communication in Statist-Theory Methods.1993.

[16]Huan-Jyh Shyur.A stochastic software reliability model with imperfect-debugging and change-point[J].The Journal of Systems and Software, 2003, 66: 135-141.

[17]P.K.Kapur, et al.Software reliability grow th modeling for errors of different severity using change point.International Jo u r n a l of Reliability, Quality and Safety Engineering, 2007, 14(4):311-326.

[18]D.N.Goswami, et al.Discrete software reliability grow th modeling for errors of different severity incorporating changepoint con cept[J].International Jou rnal of Au tom ation and computing, 2007, 4(4): 396-405.

[19]Am ir.H.S.Garmabaki, et al.Multi up-gradation software reliability grow th model with faults of different severity[A].2011 IEEE International Conference on Industrial Engineering and Engineering Management( IEEM)[C].IEEE, 2011.

[20]K.C.Chiu.A discussion of software reliability grow th models w ith time-varying learning effects[J].American Journal of Software engineering and applications, 2013, 2(3):92-104.

[21]Javaid Iqbal, etal.A software reliability grow th model with two types of learning and a negligence factor[A].2013 IEEE Second International Conference on Image Information Processing(ICIIP)(C).2013: 678-683.

[22]Yu Liu, et al.Modelling Software Fault Detection and Fault Correction Processes with Incomplete Test Data.International Conference on Information Technology and Management Science,2014.