巧解《带电粒子在匀强磁场中运动》的问题

蔡义春

【摘 要】《带电粒子在匀强磁场中运动》是高考的热点，对学生而言是一个难点。突破方法是找到粒子运动轨迹。

【关键词】速度方向确定，大小未知；速度大小确定，方向未知；巧作图

要处理好《带电粒子在匀强磁场中的运动》的问题，首先要找到带电粒子在匀强磁场中运动的轨迹。找轨迹的技巧在于掌握带电粒子在匀强磁场中运动的两种基本类型：（一）已知带电粒子在磁场中运动的方向，但不知速度大小，（二）已知带电粒子在磁场中运动的速度大小，但不知运动方向。

（一）已知带电粒子在匀强磁场中的运动方向，但不知速度大小。这一类问题的处理技巧：先过入射点作速度方向的垂线，该垂线是轨道圆半径所在的直线，然后以不同半径，沿该垂线做圆，直至找到边界。

例1、如图1所示，一足够长的矩形区域ABCD内充满磁感强度为B、方向垂直纸面向内的匀强磁场，现从矩形区域AD边的中点O处，垂直磁场射入一速度为v（大小未知）、方向与AD边夹角为30o的带正电粒子。已知粒子质量为m，电量为q，AD边长为L，AB边足够长，不计重力，求：粒子能从AB边射出的速度范围。

分析：由Bqv=m，∴v=。要想求速度，必先作圆再求半径。作圆的方法：过O点作速度方向的垂线OP，如图2。在OP上，以不同的半径作过O点的圆，直至找到边界。如图2中的圆2与上边界AB相切，由几何关系得：R+Rcos60o=，∴R=由v=，∴v=。比圆2大的圆才能与边界AB相交，如图2中的圆3，故v?。图2中的圆4与下边界CD相切，由几何关系得：R=L，v=∴v=。比圆4大的圆能从CD边射出，如图2中的圆5，故v?。综合得：?v?。

（二）已知带电粒子速度大小，但不知运动方向。由Bqv=m，∴R=即当速度大小一定时，则轨迹半径也就唯一确定，因此只需确定圆心。确定圆心的技巧：以粒子射入点为圆心，以R=为半径作圆，该圆为所有粒子轨迹圆的圆心轨迹；然后再作轨迹圆，直至找到边界。

例2.如图3所示，粒子源S能在图示纸面上360o的范围内发射速率均为v=、质量为m、电量为q的正粒子，MN是足够大的挡板，其左侧充满垂直纸面向里的匀强磁场，磁感强度为B。粒子源S到挡板的距离为L。求：被粒子击中的挡板长为多大（粒子重力不计）？ 分析：由Bqv=m∴R=。即所有射出粒子的轨道半径均为R==L，且过点S。故以点S为圆心，以L为半径作圆，如图4中的虚线圆，该圆为所有轨道圆的圆心轨迹。然后在虚线圆上任意取一点为圆心作圆，如图4中速度方向为v1的圆1。这样不断地作圆，直至找到与挡板相交的所有圆，如图5。其中速度方向为v2的圆2，打在挡板MN上的点P，此点为所有打在挡板上点的最低点（SP为圆的直径）；速度方向为v3的圆3，打在挡板MN上的点Q，此点为所有打在挡板上点的最高点。故为被粒子击中的挡板长度，如图6。由几何关系，则=R=L，=R=L。∴被粒子击中的挡板长为（+1）L

掌握了上述两种技巧，处理带电粒子在匀强磁场中运动的问题，就能如鱼得水。

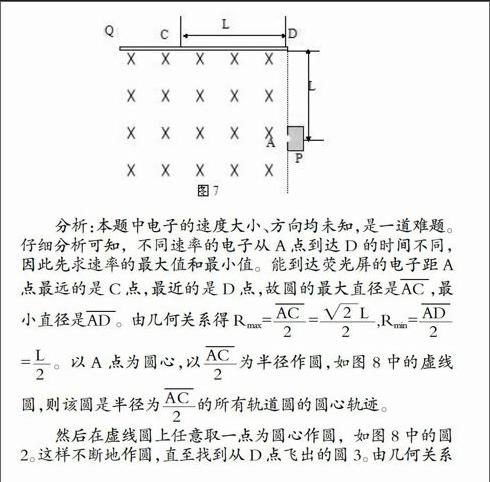
例3： 如图7所示，A处能向各个方向射出不同速率的电子。金属板P的左侧有垂直纸面向里的匀强磁场，其大小为B，面积足够大，在A点上方L处有一涂荧光粉的金属条Q，并与AD垂直。金属条Q受到电子的冲击发出荧光的部分集中CD之间，测得CD=L，电子质量为m、电荷量为e。（不计电子间的相互作用）求：能从D点飞出的电子在磁场中的飞行时间。

分析：本题中电子的速度大小、方向均未知，是一道难题。仔细分析可知，不同速率的电子从A点到达D的时间不同，因此先求速率的最大值和最小值。能到达荧光屏的电子距A点最远的是C点，最近的是D点，故圆的最大直径是，最小直径是。由几何关系得Rmax==，Rmin==。以A点为圆心，以为半径作圆，如图8中的虚线圆，则该圆是半径为的所有轨道圆的圆心轨迹。

然后在虚线圆上任意取一点为圆心作圆，如图8中的圆2。这样不断地作圆，直至找到从D点飞出的圆3。由几何关系得：∠AO3D=θ=90o，由ω==，tmin==。同理：以为半径且能从D点飞出的电子轨迹如图9中的圆2。故tmax==。综合得：能从D点飞出的电子在磁场中的飞行时间t：≤t≤