新型磁流变脂阻尼器对铁路连续梁桥地震响应模糊神经网络控制

马涌泉，邱洪兴

(东南大学土木工程学院，南京 210096)

新型磁流变脂阻尼器对铁路连续梁桥地震响应模糊神经网络控制

马涌泉，邱洪兴

(东南大学土木工程学院，南京 210096)

为解决传统磁流变液阻尼器(Magneto Rheological Fluid Damper，MRFD)磁场利用率低及磁流变液沉降导致控制特性劣化难题，提出新型阻尼器—磁流变脂阻尼器(Magneto Rheological Grease Damper，MRGD)。采用神经网络(Neural Network，NN)对足尺MRGD动力特性进行辨识，通过将改进的限幅最优(Modified Clipped－Optimal，MCO)算法整合到模糊神经网络(Fuzzy Neral Network，FNN)理论来设计适合MRGD的FNN/MCO半主动控制策略，并构建SIMULINK仿真分析平台。以典型三跨铁路连续梁桥为工程背景，分别对未控制、FNN/MCO半主动控制及线性二次型高斯(Linear Quadratic Gaussian，LQG)主动控制下桥梁各项评价指标进行分析。结果表明，所提FNN/MCO半主动控制策略对桥梁地震响应控制效果明显优于LQG主动控制策略;FNN/MCO策略较LQG策略更利于控制装置性能发挥;FNN/MCO策略稳定性、鲁棒性均明显优于LQG策略。

铁路桥梁;磁流变脂阻尼器;模糊神经网络;改进的限幅最优控制;半主动控制

近年来半主动控制技术凭借优于被动控制、能产生接近主动控制效果且无需较多外部能源优势，在桥梁结构减震领域获得广泛应用［1－3］。半主动控制过程中，控制装置的性能优劣直接影响控制效果。磁流变液阻尼器(MRFD)因具有出力大、能耗低、可控性强等优点已成为众多半主动控制装置首选［4］。而其在混合工作或流动模式下存在磁流变液沉降、有效阻尼通道短及磁场效能低的劣势，严重影响控制效果。对此，Gordaninejad等［5］合成一种磁流变脂(MRG)新材料以克服磁流变液存在的不足。MRG为胶体分散体系，主要成份有添加剂、稠化剂、铁磁性粒子、基础油及填料等。MRG在外磁场激励下流变性能连续可逆，不存在沉降、板结等不利现象［6］。Marksmeier等［7］通过分析MRGD及电流变脂阻尼器(ERGD)的力学性能，认为在低频范围内MRGD的输出阻尼力较ERGD大;Sukhwani等［8］通过分析MRGD及MRFD制动器的制动性能，认为前者输出阻尼力较后者大，且前者磁场效能较后者高。Zhu［9］通过试验分析MRGD及MRFD对转子振动的控制效果，认为前者能更显著改变转子的动力特性，控制转子振动更有效。目前，MRGD仅在车辆、机械振动控制领域有所应用，在土木工程振动控制领域研究仍为空白。土木工程结构不同于机械及车辆结构，前者质量较大，在地震中会产生较大惯性力，需对用于土木工程减震领域的MRGD进行专门设计。

本文以典型三跨铁路连续梁桥为工程背景，采用离线状态下神经网络(NN)辨识足尺MRGD的动力特性。通过将MCO算法整合到FNN主动控制策略中，设计适合MRGD的FNN/MCO半主动控制策略。并对未控制、FNN/MCO半主动控制及LQG主动控制桥梁分别进行17个评价指标的仿真计算，所得结论可供类似桥梁减震设计参考。

1 MRGD动力特性辨识

本文所提适用于桥梁振动半主动控制的新型控制装置—MRGD构造原理见图1。

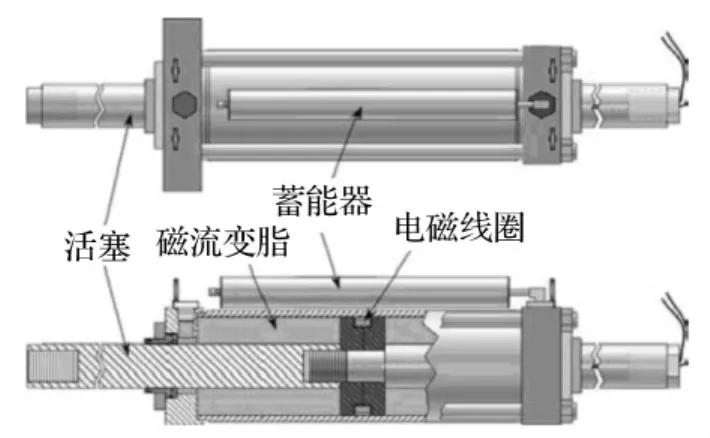
图1 MRGD的构造原理Fig.1 Structural principle of the MRGD

在外力作用下活塞迫使缸体中MRG在阻尼器中往复流动，若忽略密封摩擦压力差及MRG流动损失压力差，缸体左右两腔间压力差主要由阻尼器中MRG的流动特性决定。通过改变电磁线圈磁电流控制通道磁场强度，改变MRG流动特性，以便达到调节阻尼目的。

据磁流变脂的径向流动特点，获得微单元径向力平衡方程为

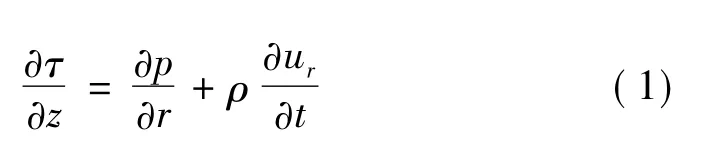
式中:τ为磁流变脂所受剪切应力;z为纵坐标;p为径向压力;r为径向坐标;ur为磁流变脂径向流动速度。

磁流变脂本构关系可用L－R模型［10］描述，即

由式(2)看出，MRG的本构关系为一组强耦合非线性方程，因此MRGD的模态特性亦为强耦合非线性。用此模型求解微分方程获取某一电压对应的结构状态时，为避免求解发散，须保证积分步长足够小(Δt＜10－4s)，因此不能用于实时控制领域。对此，本文采用Bouc－Wen模型［11］表述出力峰值为1 200 kN的MRGD力学特性，Bouc－Wen模型各参数据本文试验辨识，通过与本文试验比较准确预测阻尼力。Bouc－Wen模型力学关系可描述为

式中:U为MRGD产出的阻尼力;xd为MRGD活塞顶杆相对位移;c0为阻尼系数;h为进化变量，控制式为

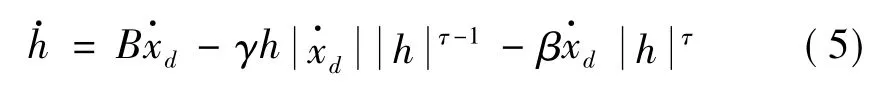
通过调整模型参数γ，β，τ，B，可保证卸载阶段线性及从屈服前到屈服后阶段光滑。

为获得理想控制效果，需保证模型有预测MRGD动力特性能力。本文提出的命令电压参数功能依靠性方程为

施加到MRGD的电压ν与一阶延迟滤波器输出u存在关系为

式中:1/η为一阶延迟滤波器时间常数，本文取η=80 s－1。

本文采用约束非线性优化法获得Bouc－Wen模型的9个参数［12］，优化法通过在MATLAB中应用序列二次规划算法执行，通过一系列尝试缩小试验值与预测值间误差测试，所得初始设置优化参数见表1。

表1 初始设置优化参数Tab.1 Optimization parameters of initial setting

对分析模型输入正弦位移及斜坡电压获得MRGD预测输出阻尼力分析值并与试验值对比，斜坡电压输入范围为0～4 V，两者对比结果见图2。由图2看出，MRGD预测输出阻尼力分析值与试验值吻合较好，表明所得优化参数可靠。

图2 MRGD预测力分析值与试验值对比Fig.2 Comparison of the tested value of predicted force of MRGD withits analytical value

具备优良非线性映射功能的NN辨识MRGD动力特性优势较大。构建网络结构及训练网络组成辨识过程两大内容，而输入层、隐含层及输出层构成网络结构三大版块。本文采用图3的NN结构辨识出力峰值为1 200 kN足尺MRGD的动力特性。该结构中输出信号为当前作用力(y0)，输入信号由三个以往电压(v)、阻尼力(f)及位移(d)构成。

图3 神经网络结构Fig.3 Neural network structure

输入向量含电压、阻尼力及位移等三部分，各部分均为连续时间步长。经验算知，本文建立的NN结构隐层节点数目为30，当位移满足d=6 sin(2πt)(cm)且电压满足ν=10 t/1.6(V)时，可得足尺MRGD的一组动力特性。据正弦位移获得训练数据，输入电压范围为0 ～10 V，并保持线性增加，对Bouc－Wen模型进行运算获得MRGD产生的阻尼力。通过辨识获所得NN预测阻尼力误差值与期望值对比见图4。

由图4可知，训练后的NN预测阻尼力误差几乎为零，且结果吻合较好。辨识NN的可靠性由随机电压、位移验证。图5为NN预测阻尼力误差值与Bouc－Wen模型所得阻尼力期望值比较。由图5看出，所得预测误差非常小，表明NN可靠性极高。

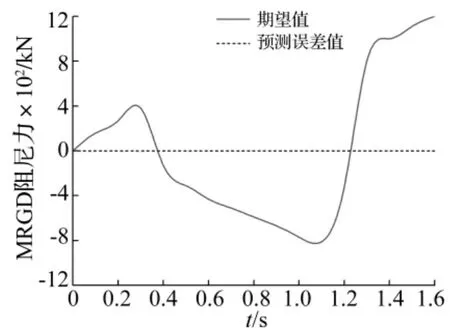
图4 期望值与预测力误差值对比Fig.4 Comparison of the error value of predicted force withits expected value

图5 期望值与误差值对比Fig.5 Comparison of the error value with expected value

2 半主动控制策略设计

2.1 受控桥梁运动方程建立

以典型三跨铁路连续梁桥为研究对象，通过对桥梁离散建立全桥有限元计算模型，见图6。图中cv，ck分别为单个MRGD粘滞阻尼系数及库仑阻尼系数，kb为未控制桥梁所用刚性铰支座弹簧刚度。设中墩、边墩均刚固于地基［13］，本文仅考虑顺桥向地震响应。

图6 连续梁桥有限元计算模型Fig.6 FEM calculation model of continuous girder bridge

设桥梁中共安装l个MRGD，则需引入n×l阶位置矩阵G，故受控桥梁系统在地震激励下的运动方程可表示为

本文用同型号MRGD，粘滞阻尼系数均为cv，即

式中:z为活塞相对缸体速度向量，与系统速度向量x·存在关系为

将式(10)代入式(9)，则Cv可表示为

受控桥梁系统在地震激励下最终运动方程为

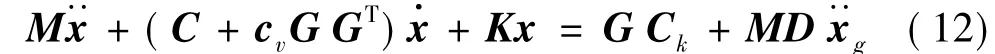
2.2 主动控制策略设计

模糊逻辑具有卓越处理模糊信息能力，可将此能力与NN强大的自适应学习、分布式信息存储及并列计算功能融合，形成模糊神经网络(FNN)［15］。本文将桥梁的状态反馈定义为加速度，设控制策略中需设置e个控制力传感器、1个地面加速度传感器及w个加速度传感器。第i时刻加速度观测输出表达式为

(1)定量分析处理T1、T2、T3、T4与CK试验结果。不同处理下的土壤浸水饱和后，测得其体积含水率数据结果如图3所示，由图可知，各处理CK、T1、T2、T3、T4组分别在水吸力为63.1 cm、67.07 cm、31.55 cm、31.14 cm和147.59 cm时达到田间持水量，且田间持水量随着生物炭施加量的增大而增大。因此施加生物炭整体上能提高土壤的持水能力。

式中:fFNN为FNN主动控制器动力学模型;r，s为模型阶次;WFNN为FNN主动控制器规则库。

选受控桥梁相对地面速度为受控输出向量，即

在中墩顶部、边墩顶部、中跨跨中梁体处及地面各布置一个加速度传感器，在中墩顶部、边墩顶部的主动控制装置处各设置一个力传感器。令模型阶次r=s= 1，则观测输出可表示为

式中:Ll(l=1，2，…，L)代表第l条规则;L为集中规则在模糊规则中总数;A(k=1，2，…，6)为输入的模糊语言变量，与第l条规则对应，定义为“PG－正大”、“NA－零”、“NG－负大”;p(k=1，2，…，6)为各输出量系数。

用高斯型函数描述语言变量的隶属度函数［16］表达式为

式中:σ，d均为用于调整隶属度函数形状参数。

用加权平均去模糊化，FNN主动控制器输出为

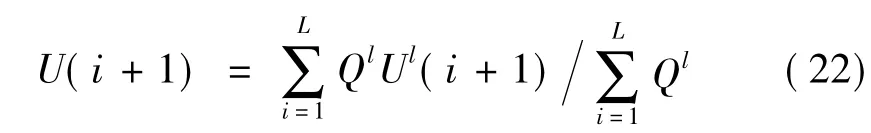
式中:Ql为第l条控制规则激励强度，表达式为

多输入少输出模糊系统为本文设计的FNN主动控制策略的显著特征，其中6个输入变量分别为当前时刻地面加速度、中墩顶部加速度、边墩顶部加速度、中跨跨中梁体加速度及中、边墩顶部MRGD产出的阻尼力;输出变量为MRGD在后一时刻产出的阻尼力预测值。用LQG主动控制计算结果对FNN主动控制策略进行离线训练。准则为NN需被第i步训练，第i+1步的控制力U(i+1)才能被预测。在FNN中，网络权值及隶属度函数参数由混合学习算法训练获得。

2.3 半主动控制算法描述

半主动控制装置MRGD不能直接将主动控制提供的最优控制力作为出力，也不能被控制器调整到任意所需状态，只能调整施加的电压促使MRGD的出力尽可能贴近最优控制力。本文采用改进的限幅最优(MCO)半主动控制算法［14］切换施加于MRGD的电压。电压切换状态可表示为

式中:νj为施加于第j个MRGD的电压;Vcj为控制电压; H(*)为Heaviside阶跃函数;Uj为当前所得MRGD控制力;Umax为MRGD最大产出阻尼力;Ucj为主动控制策略所得最优控制力;μj为电压转换成力的增益;Vmax为施加到电流驱动器电压，该驱动器与MRGD中磁流变效应饱和度对应。

本文将MCO半主动控制算法整合到FNN主动控制策略中，形成适合MRGD的FNN/MCO半主动控制策略，并采用MTALAB语言建立地震激励下铁路桥梁振动FNN/MCO半主动控制的SIMULINK仿真分析流程，见图7。FNN主动控制器构造见图8。

图7 桥梁振动FNN/MCO半主动控制的SIMULINK流程图Fig.7 SIMULINK flow diagram of FNN/MCO semi－active control for suppressing the bridge vibration

图8 FNN主动控制器的构造Fig.8 Structure of FNN active controller

3 仿真分析

3.1 系统参数

采用FNN/MCO控制时，在桥墩顶部与梁体间布置足尺MRGD，标定最大出力为1 200 kN，活塞最大冲程为20 cm(±10 cm);LQG主动控制装置为压电陶瓷作动器，标定最大出力、最大冲程与MRGD相同。分别选El－Centro波(S90W)、Loma－Prieta波(N90E)、Kobe波 (N90E)及Northridge波(N90E)等4条加速度记录为地震激励，简称为E、L、K、N波。其中E、L为近场地震波，K、N为远场地震波，其峰值加速度分别为2.147 m/s2、5.964 m/s2、6.170 m/s2、5.935 m/s2。桥梁跨径为30 m+30 m+30 m，墩高8 m，桥梁计算参数见表2。边、中墩计算参数相同。梁体及支座位移限值均为6 cm，梁体与墩顶相对位移限值为5 cm。

表2 桥梁结构计算参数Tab.2 Computation parameters of the bridge structure

分别对未控制、FNN/MCO半主动控制桥梁输入El－Centrol地震波进行响应仿真分析，获得两种控制方案下Q1(中跨跨中梁体位移)、Q2(中跨跨中梁体加速度)、Q4(边墩墩顶位移)及Q5(中墩墩底剪力)对比时程见图9。由图9看出，采用FNN/MCO半主动控制后，Q1、Q2、Q4、Q5等评价指标较未控制均明显降低，FNN/MCO控制下评价指标峰值分别仅为未控制的52.6%、31.5%、25.1%及26.1%。可见在E波激励下，本文FNN/MCO半主动控制策略减震效果良好。

图9 未控制与FNN/MCO半主动控制桥梁地震响应对比时程Fig.9 Seismic responses time history comparison of non－control bridge with FNN/MCO semi－active control bridge

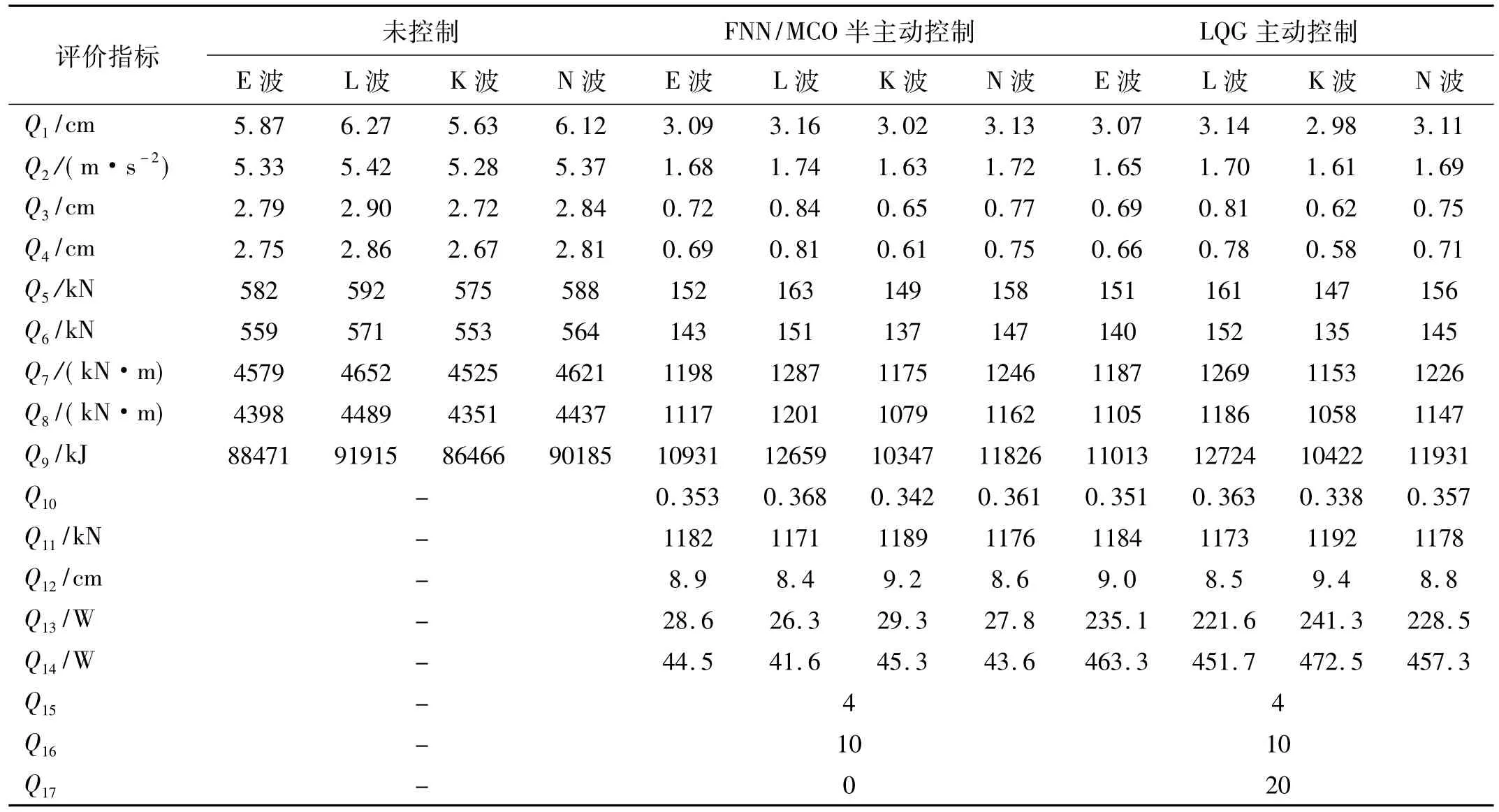
表3 四条地震激励、三种控制方案下性能评价指标Tab.3Performance evaluation criteria of three control schemes subjected to four seismic excitations

图10 四条地震激励、三种控制方案下支座位移峰值Fig.10 Peak bearing displacements of three control schemes subjected to four seismic excitations

表3、图10分别为未控制、FNN/MCO半主动控制及LQG主动控制等方案桥梁在4条地震激励下各评价指标(Q1～Q17)峰值及支座位移峰值。由表3看出，FNN/MCO半主动控制及LQG主动控制的桥梁在4条地震激励下Q1、Q2、Q3(中墩墩顶位移)、Q4、Q5、Q6(边墩墩底剪力)、Q7(中墩墩底弯矩)、Q8(边墩墩底弯矩)等评价指标峰值较未控制均显著降低。同条地震激励下FNN/MCO的Q1～Q8较LQG略大。可见FNN/MCO策略不仅能显著降低桥梁的地震响应，且减震效果接近LQG策略。表明本文的FNN/MCO策略可靠性极高。

在4条地震激励下，FNN/MCO及LQG控制桥梁的Q9(结构耗能量)较未控制均显著降低。在同条地震激励下FNN/MCO结构耗能量较LQG小些。由于输入桥梁的总地震能为定值，结构耗能量越小，表明控制装置耗能量越大，即FNN/MCO策略较LQG更利于控制装置耗能特性发挥;FNN/MCO控制的Q10(受控桥梁与未控桥梁出现塑性铰破损个数比值)较LQG略大。即FNN/MCO、LQG控制的桥梁均已进入塑性阶段，且前者用于延性耗能的塑性铰较后者略少。

在同条地震激励下，FNN/MCO的Q11(控制装置实际产出的最大控制力)较LQG略小，即在FNN/MCO控制的MRGD最大出力接近LQG的压电陶瓷驱动器的最大出力;FNN/MCO的Q12(控制装置实际产生的最大冲程)较LQG略小。无论FNN/MCO或LQG，其最大冲程均在标定范围内(±10 cm)。故整个地震过程中，控制装置能始终保持良好工作状态;FNN/MCO半主动控制的Q13(控制装置所需总功率)较LQG小很多。LQG策略为产出预期控制力，需外界提供大量稳定能源，由于桥梁进入塑性阶段，其动力特性会发生变化，此时LQG策略很难保证控制系统闭环稳定。而FNN/ MCO策略无需外界提供较多能源，故其控制系统稳定性良好。可见FNN/MCO策略的稳定性明显优于LQG;FNN/MCO策略的Q13/Q14(Q14为结构振动控制所需总功率)较LQG的大，即FNN/MCO策略的控制装置能量利用率高于LQG，且前者的Q14较LQG少得多。因此本文的FNN/MCO半主动控制策略节能高效。FNN/MCO控制及LQG控制的Q15(所需控制装置数目)、Q16(所需传感器数目)数值相同，但FNN/MCO所需Q17(计算资源量，用控制算法所需离散状态向量维数表征)为零，表明FNN/MCO策略的显著优势为无需任何计算资源。对在线实时控制而言，可避免控制器在运算过程中产生时滞。

由图10看出，FNN/MCO策略(方案Ⅱ)及LQG策略(方案Ⅲ)在4条地震激励下支座位移峰值较未控制(方案Ⅰ)均明显降低，其中FNN/MCO、LQG在L、K波激励下的支座位移峰值分别为未控制的50.4%、50. 6%及50.1%、52.9%;L、N波激励下未控制桥梁支座位移峰值已超出限值，会对桥梁伸缩、限位装置造成破坏;在同条地震激励下，FNN/MCO与LQG控制的支座位移峰值相差很小。

图11为El－Centro地震激励下的FNN/MCO半主动控制策略和LQG主动控制策略所产出的控制力对比时程。由图11看出，FNN/MCO策略的MRGD控制力曲线平滑，无任何抖振现象发生。而LQG策略下的压电陶瓷驱动器控制力曲线多处出现抖振，会对LQG控制器性能造成不利影响。

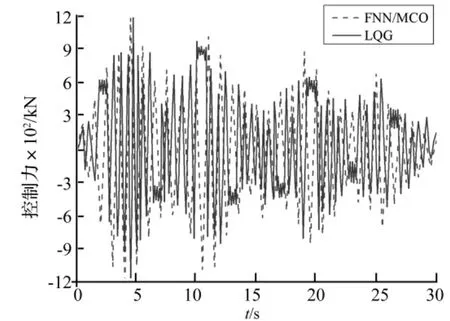
图11 FNN/MCO与LQG策略控制力对比时程Fig.11 Time history comparison of LQG strategy with FNN/MCO strategy

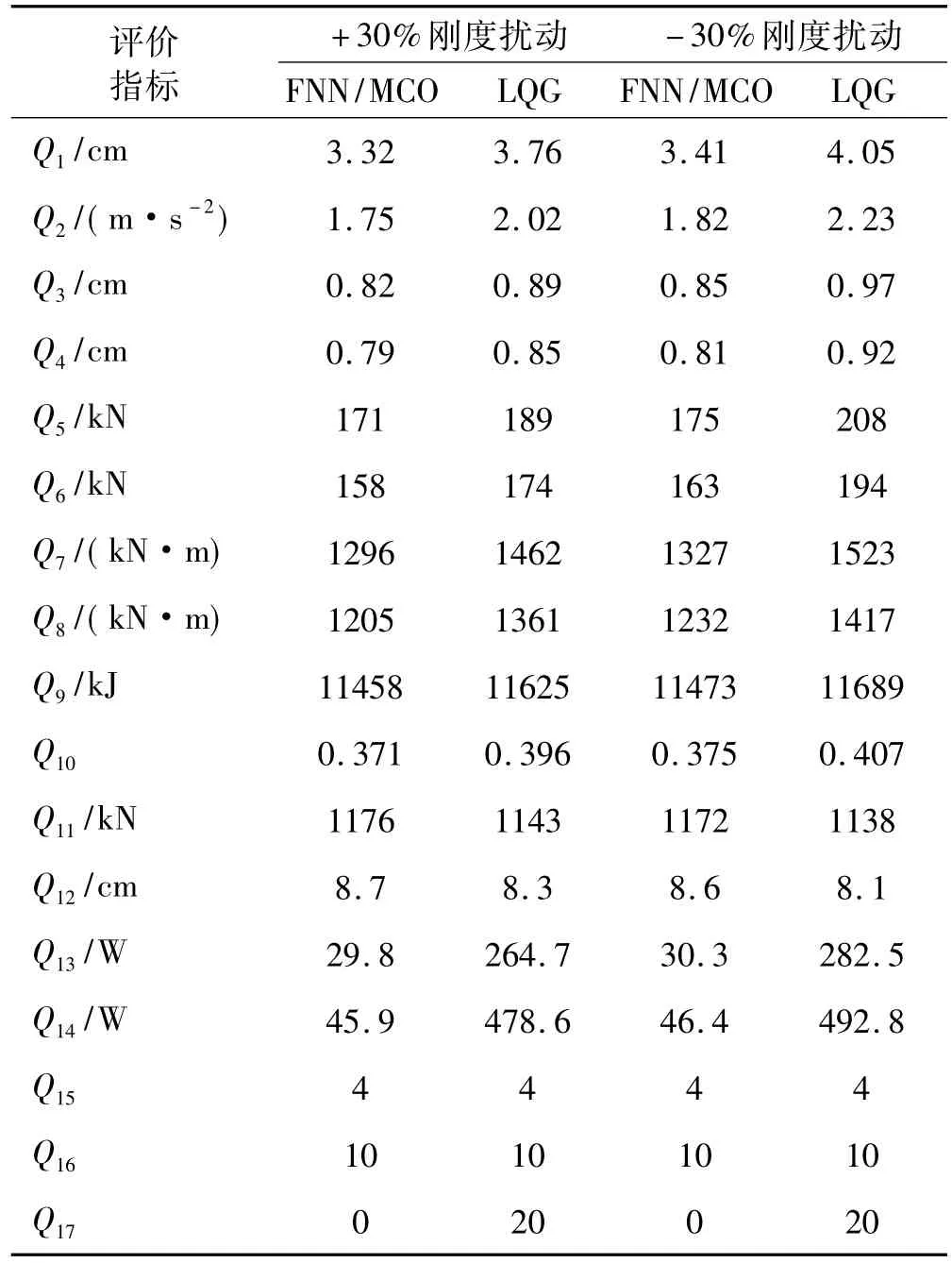
表4 ±30%刚度摄动下各评价指标平均值Tab.4 Average value of various evaluation criteria due to±30%stiffness perturbed

本文通过分别计算FNN/MCO、LQG控制桥梁的初始刚度在发生±30%摄动时4条地震激励下各评价指标平均值比较两种策略的鲁棒性。两种控制策略各指标平均值见表4。由表4看出，FNN/MCO控制的各地震响应指标(Q1～Q10)、损伤指标(Q9、Q10)均明显小于LQG控制，且FNN/MCO策略控制装置性能指标(Q11～Q14)较LQG策略优越。可见在桥梁刚度存在不确定性时，FNN/MCO控制器性能明显优于LQG，故FNN/ MCO控制器的鲁棒性明显优于LQG控制器。

4 结论

(1)本文所提适合MRGD的FNN/MCO半主动控制策略对桥梁地震响应减震效果非常好，计算结果与LQG主动控制策略非常接近;FNN/MCO策略较LQG更利于控制装置发挥耗能作用，且FNN/MCO策略用于延性耗能的塑性铰个数较LQG略少;FNN/MCO策略的控制装置最大出力、最大冲程均接近标定峰值，MRGD在震后仍能正常使用;FNN/MCO策略所需外界能量较LQG少得多，且FNN/MCO对能量的利用率较LQG高得多。

(2)FNN/MCO半主动控制策略所需控制装置及传感器数目均与LQG主动控制策略相同。采用FNN/ MCO策略对桥梁进行振动控制，无需任何计算资源，可避免控制器运算造成的时滞，而LQG策略却需较多计算资源;LQG策略需外界提供大量稳定能源，易引起闭环失稳，而FNN/MCO策略稳定性极高;FNN/MCO策略的鲁棒性明显优于LQG，前者控制力曲线非常平滑，后者控制力曲线出现多处抖振现象。

［1］Maddaloni G，Caterino N，Occhiuzzi A.Semi－active control of the benchmark highway bridge based on seismic early warning systems［J］.Bulletin of Earthquake Engineering，2011，9(5):1703－1715.

［2］Ali S，Ramaswamy A.Optimal dynamic inversion－based semiactive control of benchmark bridge using MR dampers［J］. Structural Control and Health Monitoring，2009，16(5):564－585.

［3］Erkus B，Abe M，Fujino Y.Investigation of semi－active control for seismic protection of elevated highway bridges［J］. Engineering Structures，2002，24(3):281－293.

［4］Ali S F，Ramaswamy A.Optimal dynamic inversion－based semi－active control of benchmark bridge using MR dampers［J］.Structural Control and Health Monitoring，2009，16(5):564－585.

［5］Gordaninejad F，Kavlicoglu B M.Study of a magnetorheological grease(MRG)clutch［C］.//Proceedings of the SPIE 14th International Symposium on:Smart Structures and MaterialsandNondestructiveEvaluationandHealth Monitoring，San Diego，2007.

［6］Park B O，Park BJ，Hato M J，et al.Soft magnetic carbonyl iron microsphere dispersed in grease and its rheological characteristics under magnetic field［J］.Colloid and Polymer Science，2011，289(4):381－386.

［7］Marksmeier T M，Gordaninejad F，Wang E L，et al.Design and performance of an electro－rheological grease(ERG) shock absorber［J］.International Journal of Modern Physics B，1999，13(14):2135－2142.

［8］Sukhwani V K，Hirani H.A comparative study of magnetorheological－fluid－brake and magnetorheological－grease－brake［J］.Tribology Online，2008，3(1):31－35.

［9］Zhu C S.Experimental investigation on the dynamic behavior of a disk－type damper based on magnetorheological grease［J］.Journal of Intelligent Material Systems and Structures，2006，17(8):793－799.

［10］Laun H M，Rady M，Hassager O.Analytical solutions for squeeze flow with partial wall slip［J］.Journal of Non－Newtonian Fluid Mechanics，1999，81(1):1－15.

［11］Yoshida O，Dyke S J，Giacosa L M，et al.Experimental verificationoftorsionalresponsecontrolofasymmetric buildings using MR dampers［J］.Earthquake Engineering and Structural Dynamics，2003，32(13):2085－2105.

［12］Yi F，Dyke S J，Caicedo J M，et al.Experimental verification of multi－input seismic control strategies for smart dampers［J］.Journal of Engineering Mechanics，2001，127(11): 1152－1164.

［13］Jangid R S.Seismic response of isolated bridges［J］.Journal of Bride Engineering，2004，9(2):156－166.

［14］Yoshida O，Dyke S J.Seismic control of a nonlinear benchmark building using smart dampers［J］.Journal of Engineering Mechanics，2004，130(4):386－392.

［15］Mosleh M，Otadi M，Abbasbandy S.Evaluation of fuzzy regression models by fuzzy neural network［J］.Journal of Computational and Applied Mathematics，2010，234(3): 825－834.

［16］Hameed I A.Using gaussian membership functions for improving the reliability and robustness of students＇evaluation systems［J］.Expert Systems with Applications，2011，38(6):7135－7142.

Fuzzy neural network control to suppress seismic responses of continuous girder railway bridges using new magneto rheological grease damper

MA Yong－quan，QIU Hong－xing
(College of Civil Engineering，Southeast University，Nanjing 210096，China)

In view of the problems of low utilization rate of magnetic field and degraded control characteristic due to sedimentation of magneto rheological fluid in traditional magneto rheological fluid damper(MRFD)，magneto rheological grease damper(MRGD)as a new type of damper was proposed.The neural network(NN)was employed to identify the dynamic characteristics of a full－scale MRGD，the FNN/MCO semi－active control strategy for MRGD was designed by integrating the modified clipped－optimal(MCO)algorithm with the fuzzy neral network(FNN)theory，and the SIMULINK simulation analysis platform corresponding to FNN/MCO strategy was constructed.Taking the typical threespan continuous girder railway bridge as engineering background，the various evaluation criteria for the bridge with noncontrol，FNN/MCO semi－active control and active control based on linear quadratic Gaussian(LQG)strategy were analyzed respectively.The analytical results show that the control effect on seismic responses of bridge with the FNN/MCO semi－active control strategy proposed is obviously superior to those with LQG active control strategy.Comparing with LQG strategy，the FNN/MCO strategy can more obviously contribute to the performance exertion of control devices.The stability and robustness of the FNN/MCO strategy are both superior to those of LQG control strategy.

railway bridge;magneto rheological grease damper;fuzzy neural network;modified clipped－optimal control algorithm;semi－active control

O328;U441+.3

A

10.13465/j.cnki.jvs.2015.02.012

“十二五”国家科技支撑计划重点资助项目(2012BAJ14B00);国家自然科学基金重点资助项目(51078077)

2013－06－07修改稿收到日期:2014－03－05

马涌泉男，博士生，1984年7月生

邱洪兴男，博士，教授，博士生导师，1962年4月生邮箱:qiuhx@seu.edu.cn