摩托车车架动态特性分析及结构对比改进

朱玉强，饶建强

（1.广东交通职业技术学院，广东广州 510650；2.华南理工大学广东汽车工程重点实验室，广东广州 510640）

摩托车设计开发过程中关键问题之一是整车减振，车身振动水平的高低直接影响驾驶员和乘员的舒适性体验。车架是摩托车主要的承载、连接和传力部件，既承载乘员和货物的重量，又承受行驶过程中路面不平度和发动机的激励，并通过传动装置、减震器和坐垫传递到乘员。为降低车身振动，改善驾乘者舒适性体验，应分析车架动态特性即模态特性，在此基础上进行结构改进[1-2]。

模态分析一般有解析法和实验法两种[3-4]，前者主要依赖于计算机软件进行仿真分析，实验法是利用各种实验设备开展车架的自由模态实验。两者结合可以准确分析摩托车车架结构动态特性，为进一步的改进设计提供参考。某企业新款摩托车样车行驶过程中存在振动程度过大、驾驶员舒适性体验较差的现象。选择市场反映较好的本田150摩托车车架，通过CATIA和HYPER⁃MESH建立该款车车架及本田摩托车车架的计算分析模型，利用实验法和解析法分析两款车架动态特性，进行结构对比并最终提出改进方案，从而为后续的改良试制提供参考。

1 车架仿真模态分析

1.1 CAE仿真模型的建立

利用ATOS光学扫描仪对车架进行多个方位、多个角度扫描，得到车架外形点云文件。在此基础上利用CATIA进行建模，得到车架的三维模型。将模型导入HYPERMESH中，进行有限元分析的前处理。由于摩托车车架主要是由截面尺寸不同的钢管和板件通过焊接和螺栓连接组成，且钢管和板件在厚度方向上的尺寸远远小于其长度和宽度尺寸，因此对原结构进行抽中面处理，划分二维网格。选用附厚度的壳单元（PSHELL）进行模拟，厚度值是实际测量车架得到的各个组件的钢板厚度。使用的材料密度为7.8×103kg/m3，弹性模量为210 GPa，泊松比为0.28。利用Auto⁃mesh功能对网格进行自动划分，然后对不符合要求的网格进行逐步优化，利用rbe2刚性单元模拟现实中的缝焊连接，将焊缝区域节点连接起来。所建立的两款车架有限元模型如图1所示。

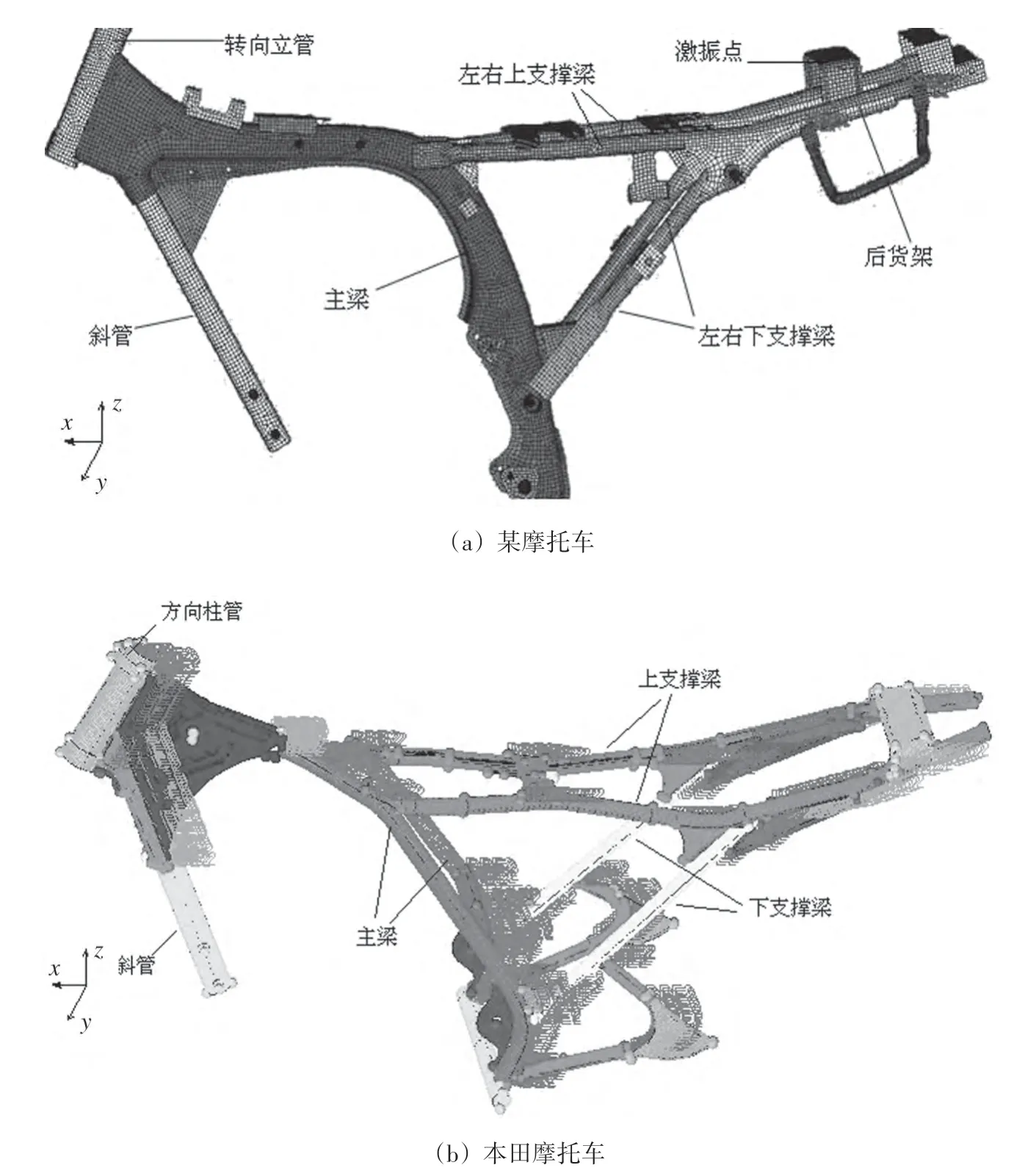
图1 车架有限元模型

1.2 车架动力学微分方程[5-6]

摩托车车架属于多自由度连续弹性体结构，其固有频率和主振型只与结构的刚度特性和质量分布相关，在通常的物理坐标系中，可将车架振动的微分方程可表示为：

其中：[M]--系统质量矩阵；[K]--系统刚度矩阵；{}u--位移向量；{}ü--加速度向量。由于弹性体的自由振动总是可以分解为一系列简谐振动的叠加，因此式（1）的解为

将式（2）代入式（1），得到特征值方程：

若结构发生自由振动，则该式应当有非零解，则其系数矩阵行列式为零，即

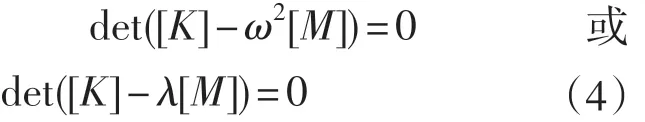
式 （4） 中 λ=ω2，求解该多项式得到一组特征值解λi，将式（4）改写为

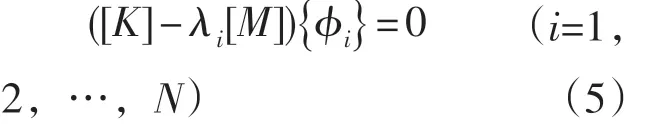
其中：N—刚度矩阵[K]的维数，即自由度数；λi为第i个特征值；{ϕi}为λi对应的第i个模态向量。

1.3 仿真结果对比分析

摩托车车架结构的动态特性主要取决于低阶模态，高阶模态振型对结构动特性的影响较小。考虑摩托车在行驶过程中可能受到的路面激励及发动机激励的频率范围以及摩托车常用车速，选取0～300 Hz作为计算频率区间。将有限元分析模型导入大型求解器NASTRAN，选用兰索士法（LANCZOS）进行计算，分析得出两车架300 Hz以下的固有频率和振型。利用HYPERVIEW打开文件查看结果，得到两车架前6阶固有频率如表1所示。

由以上分析结果可知：0～300 Hz范围内，某摩托车车架有6阶模态，本田摩托车车架有5阶模态，且本田摩托车车架前5阶模态频率比某摩托车车架模态频率明显高很多。分析两者的主振型图发现：本田摩托车车架整体振幅较小，结构设计合理；某摩托车车架整体振幅大于本田车架，尤其是斜管处振动最大。分析原因是由于车头刚度较低，高速行驶时容易造成车头扭摆，应进行改进。

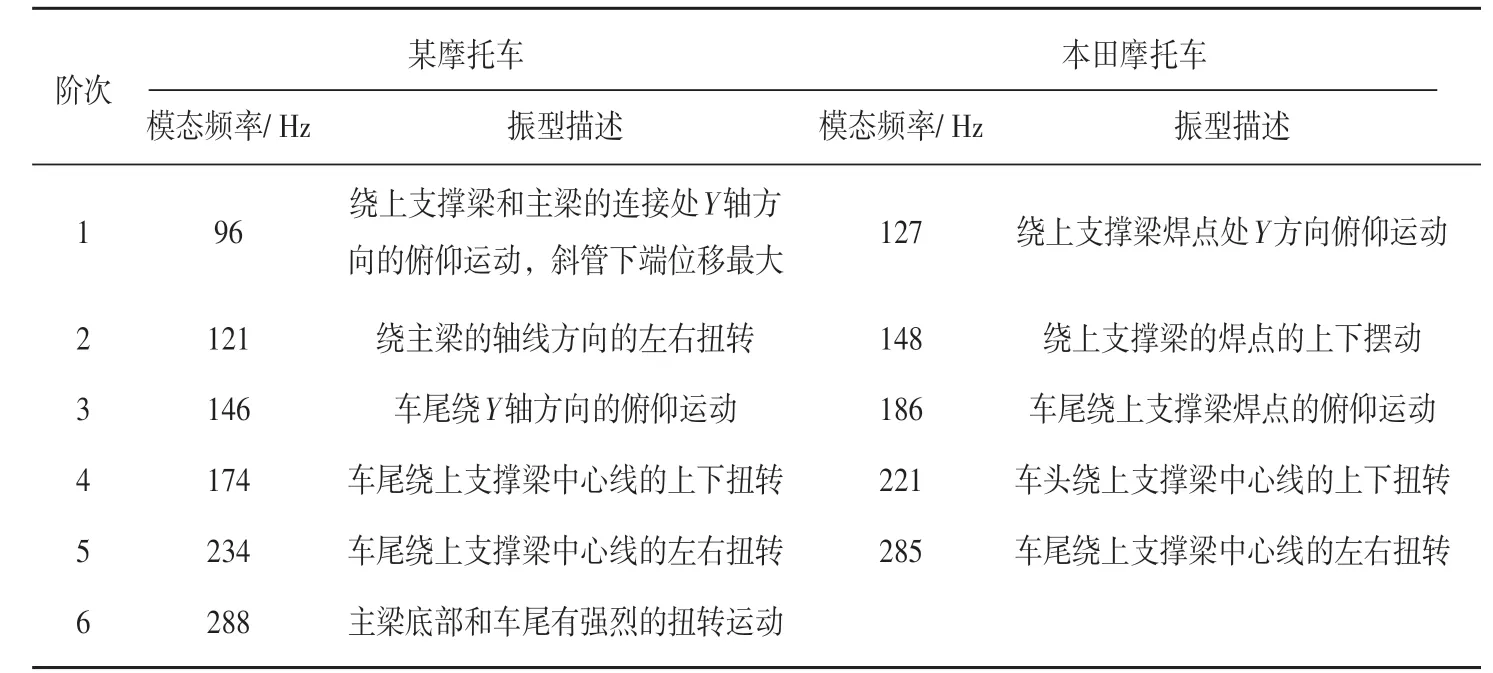
表1 某摩托车与本田摩托车车架仿真固有频率对比

2 实验模态分析

模态实验可用于研究线性系统振动特性，其实验原理为：使用激振器或者力锤对研究对象进行激励，测试出测点的响应值。然后根据被测系统特性，选择不同的模态参数识别方法，一般有时域法和频域法，识别研究对象的模态参数。实验模态结果精度主要取决于操作人员的熟练程度及仪器设备的测量精度，与计算模态结果之间是互为验证的关系。实验测量系统一般包括：激振力系统、响应采集系统、数据分析及后处理系统。本次实验采用的设备为DH5922数采系统的信号发生模块、功率放大器和激振器；力传感器、加速度传感器和数据采集系统以及东华DH⁃MA模态分析软件。

2.1 实验条件

用柔软的橡皮绳将车架悬吊，使其处于水平自由状态。实验采用单点激振多点拾振的方法，利用激振器激励，激振器采用固定安装方式，与沉重的铁板相连。建立摩托车坐标系：取摩托车前进方向为X轴正向，摩托车前进方向的左侧为Y轴正向，竖直方向为Z轴正向。激振器的安装位置及实验现场见图1。激振时采用burst random猝发随机信号，在车架后部行李架中部位置沿Z向进行激励。测点按照车架中心面对称布置，建立的车架测点线框模型及测点位置分布如图2、3中所示。

2.2 结果对比分析

利用三向加速度传感器测量各个测点在x、y和z向的加速度，计算各个测点到激励点的传递函数，然后采用传递函数的集总平均进行模态定阶，分析所得的前6阶实验模态参数与仿真模态参数对比如表2所示。

由表2中数据分析可得：两种摩托车车架通过仿真分析得出的前6阶模态频率与实验结果相差较小，在可允许的误差范围内，主要振型基本一致，证明所建立的仿真模型精确度较高，可用于进一步的分析计算。仔细观察某摩托车前6阶实验模态振型可知：第1阶为弯曲模态，车头部分沿Y轴方向的俯仰运动，主梁振动幅度较大；第2阶为扭转模态，下支撑管及斜管扭转摆动、弯曲明显，3～6阶振型中均出现上支撑管扭摆及弯曲明显，振动幅度过大的情况，需要改进。

图2 车架模态实验

图3 车架线框模型及测点位置

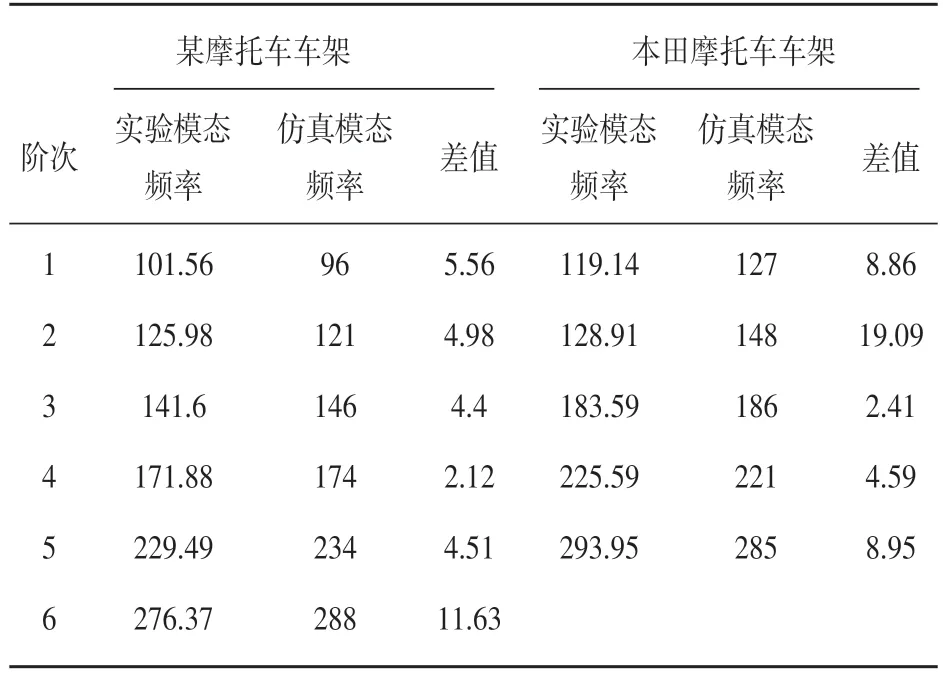
表2 两车架实验模态频率与仿真模态频率对比Hz

3 改进方案

对比两种摩托车车架结构，本田摩托车车架主梁分为两根，与斜管、转向柱管之间通过两块三角钢板和一块方向钢板焊接成为一体，某摩托车车架主梁、斜管和方向柱管是直接焊接在一起，没有任何加强部件。测得本田摩托车方向柱管外径为48.4 mm，斜管外径为33 mm，上支撑梁外径为22.3 mm，下支撑梁外径为25.4 mm；某摩托车方向柱管外径为45.6 mm，斜管外径为32 mm，上下支撑梁外径均为22.1 mm，均小于本田摩托车车架对应结构；因此考虑通过增设加强部件以及增加管材厚度来提高某摩托车车架整体刚度。

改进方案：将主梁增厚1 mm，将上支撑梁和下支撑梁也增厚1 mm；在斜管和主梁之间的夹角位置增加一块三角形的钢板，板厚与主梁下边原板厚一致，加强主梁与斜管之间的连接和支撑；主梁与两根上支撑梁之间夹角位置分别增加一块三角形钢板进行加固，厚度为3 mm；主梁与两根下支撑梁连接位置增加一块厚度为3 mm的转角钢板，加强两根下支撑梁之间的连接及其和主梁之间的连接。

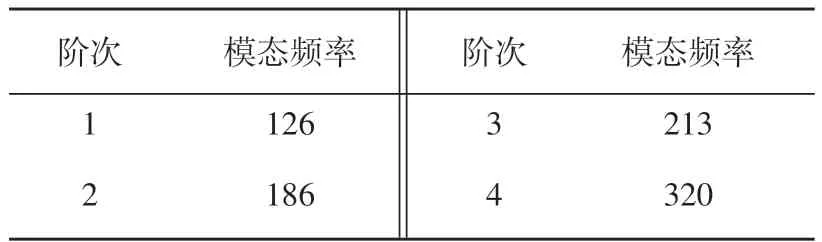
表3 车架改进后前4阶仿真固有频率Hz

将改进后的仿真模型输入到NASTRAN进行计算，得到改进后车架前四阶固有频率如表3中所示。在0～300 Hz范围内只有三阶固有频率，因此只考虑前三阶固有频率主振型。通过HYPER⁃VIEW观察前三阶振型，如图中4、5、6所示：一阶振型为车架绕上支撑梁和主梁的焊点Y轴方向的前后俯仰运动；二阶振型为车尾绕上支撑梁的焊点的扭转运动；三阶振型为车尾和车头围绕主梁的焊点的扭转运动。

图4 一阶主振型

图5 二阶主振型

图6 三阶主振型

4 结论

改进后的车架与改进前相比，改进后车架主要有前三阶固有频率，比改进前少了三阶，各阶固有频率比原来都有大幅度提高，并且振幅也有所减小。因此可见，同时增加主梁、上支撑梁和下支撑梁厚度对车架结构影响最大，改进后的车架在结构上得到了明显加强，振动得到了改善。

［1］张尚先，程国飞.管壳单元和管单元摩托车车架模态分析与实测研究［J］.机械设计与制造，2010（6）：190-192.

［2］幸芦笙，欧阳兆彰，王大承.250QT-9N摩托车车架特性分析［J］.机械设计与制造，2008（4）：142-143.

［3］黄泽好，徐中明，张志飞.摩托车车架振动特性分析［J］.农业机械学报，2006（9）：208-210.

［4］徐中明，张志飞，周坤，等.摩托车振动舒适性分析与改进 ［J］.中国机械工程，2007，18（24）：3009-3013.

［5］肖雄.电动摩托车车架结构优化设计分析［D］.重庆：重庆大学，2014.

［6］沃德·海伦，斯蒂芬·拉门兹，波尔·萨斯·白代同，郭继忠译.模态分析理论与试验［M］.北京：北京理工大学出版社，2001.