8mm厚高强钢板矫直策略的模拟仿真研究
杨晓臻,赵志毅,孙 林,林 玮
(1.宝山钢铁股份有限公司,上海200941;2.北京科技大学 材料科学与工程学院,北京100083;3.中国兵器工业新技术推广研究所,北京100089;4.北京科技大学 新材料技术研究院,北京100083)
矫直是精整的核心工序,辊式矫直机是保证板带材平直度、改善板带材残余应力分布的重要设备。选择合适的矫直策略、制订合理的矫直机矫直工艺参数是保证产品质量的关键[1]。由于高强钢板的强度较高,塑性较低,在设计矫直工艺时需要同时考虑设备的负荷,保证生产过程的稳定和安全[2]。
随着计算机应用水平的发展,计算机模拟仿真技术在金属弹塑性变形领域得到了进一步的应用[3]。国内一些学者应用有限元模拟仿真技术对辊式矫直机的矫直工序进行了研究,研究了不同矫直工艺对钢板板形的影响[4-6]。
本文用ABAQUS有限元模拟仿真软件对矫直过程进行模拟,研究矫直策略、矫直工艺变化对矫后板形和残余应力的影响,为矫直工艺的优化提供依据,以改善产品质量,提高生产稳定性。
1 有限元模拟仿真模型的建立和验证
1.1 ABAQUS有限元模拟仿真模型的建立
参考某钢厂的生产实际,矫直过程模拟仿真参数如下:矫直辊间距为220mm,辊径为200mm,工作辊数量为17个,矫直辊转速为3rad/s,辊身长度为2 350mm。待矫板材的外形尺寸为2 200mm×1 200mm×8mm。为了模拟现场的板形,设其浪高为50mm。材料属性特征:屈服强度Rp=980 MPa,弹性模量E=197GPa,泊松比v=0.3,摩擦因数f=0.2,密度为7.8×103kg/m3。塑性值由拉伸试验获得。
根据ABAQUS分析类型划分,钢板矫直工艺的模拟属于静态非线性结构分析。钢板选择八结点线性减缩积分六面体单元(C3D8R单元),材料各向同性。矫直辊选用三维解析刚体,不需要进行单元的划分。钢板的单元设置为线性减缩积分,即在单元中心包含1个积分点。ABAQUS在线性减缩积分中引入了“沙漏刚度”来限制沙漏模式的扩展。选择矫直辊作为第1表面,钢板作为第2表面,用罚函数法作为接触界面算法。将17个矫直辊和钢板装配成几何模型,如图1所示。经统计,共有7 920个网格。

图1 矫直过程有限元模拟仿真模型
边界条件和预定义场设定如下。
1)限定矫直辊沿X、Y、Z轴位移的自由度及沿X、Z轴转动的自由度,这样矫直辊只能围绕Y轴旋转。
2)设定矫直辊转速3rad/s作为边界条件,这与现场的矫直速度相当。
3)限定钢板沿Y轴(即沿辊身长度方向)平移的自由度和其沿X、Z轴转动的自由度,这样可以使钢板能够平直的通过矫直机,避免在矫直机内的横向移动。
4)给钢板一个初始的助推力,方便其咬入。
为了施加实测的应力作为初始应力,需要编写inp文件,赋予钢板应力值。为使钢板的初始应力状况更加接近真实,对一块未经过矫直的钢板沿着板宽方向进行残余应力测试,测试点达到40个,然后根据所得到的应变值,计算出40个测试点的应力值(见表1),随后将钢板沿板宽方向分为40等份,再将每份的应力值写入inp文件中。

表1 钢板初始应力输入值
以点1为例,编写第1条钢板的初始应力值,写入ABAQUS/CAE的inp文件之中。其inp文件写法如下:

其余各点以此类推。
1.2 矫直工艺的设计
根据不同的矫直策略,设计如下3种矫直工艺。
1)大压下矫直工艺。钢板的板形往往不是单次浪形,而是复杂的高次浪形。反弯曲率越大,钢板各部分弹复曲率差值越小,即钢板弹复后的残余曲率变化范围也就越小。根据这种策略,在第2和第3辊上采用很大的相对反弯曲率,使轧件各部分的总弯曲变形曲率达到很大数值,即可迅速地将残余曲率减小,使整个轧件长度方向上几乎成为单值曲率。经过几次反弯,轧件趋于平直,达到矫直目的。
2)小压下矫直工艺。初始道次的压弯量仅仅消除钢板的最大初始曲率,而后续道次仅仅消除前一道次的残余曲率。这种压下方式的能耗最小,但是在实际生产中难以实现。
3)线性递减矫直工艺。由于该矫直机的辊数较多,不必要在第1和第2辊处消除所有的初始曲率,因此,将初始反弯曲率设为大压下矫直工艺的80%,通过反复多次弯曲,使残余曲率消除为0。
具体矫直工艺设定见表2。
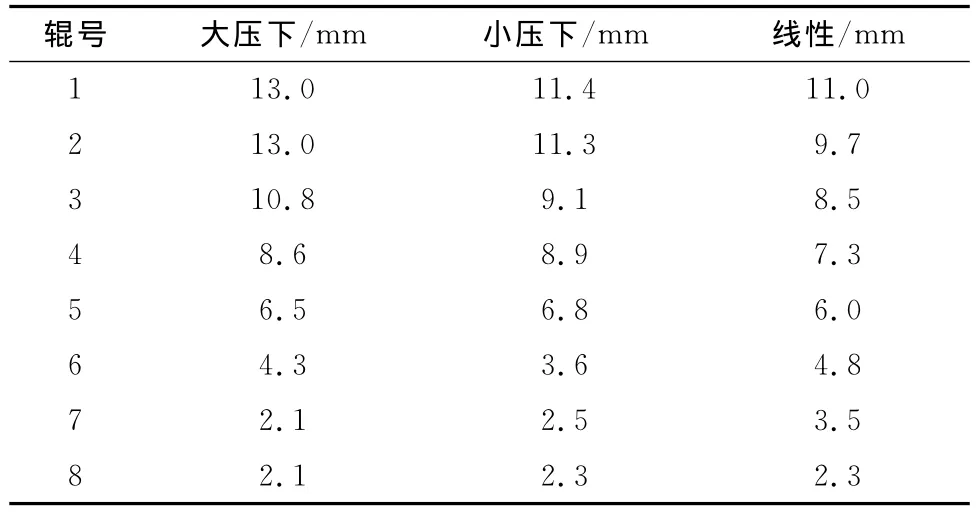
表2 理论推导矫直工艺压下量分配
1.3 模型的验证
首先,将通过实测获得的初始应力编写为inp文件的形式写入到初始钢板当中,使钢板带有初始残余应力;然后,按照表2所述的大压下矫直工艺对矫直工作辊进行调节;最后,进行大压下矫直工艺的模拟。矫直前、后钢板残余应力分布如图2和图3所示。从图中可以看出,钢板的整体应力水平降低了,而且应力的分布情况变得均匀了,说明矫直模拟过程很好地反映了矫直工艺能够降低应力水平,并且均匀钢板的残余应力分布情况。

图2 矫直前钢板残余应力分布云图

图3 矫直后钢板残余应力分布云图
在现场将各矫直辊压下量设定为大压下矫直工艺的压下量,对矫后钢板用小孔法测试沿着板宽方向残余应力的分布。
读取矫直之后的ODB文件,导出距离钢板头部1 000mm处垂直轧向的1条直线上的10个节点的纵向应力值,与实测的钢板中部的精矫后的应力分布情况进行对比,如图4所示。从图中可以看出,模拟后的应力分布情况与实测得到的分布情况基本相似,这说明矫直模型各参数采集较为准确,矫直模型较为准确地反映了真实的矫直过程。而模拟值小于实测值的原因,一方面是模型中钢板的屈服强度是真实强度的最小值,导致模型中钢板的整体强度低于真实值,这更有利于应力的释放;另一方面模拟过程的矫直辊是刚性辊,在矫直过程中没有弹跳,而现实中,矫直辊是有弹跳现象的,这使得模拟过程的压下量要大于现实值,这样就更有利于应力的释放。

图4 矫直前、后钢板沿板宽方向残余应力分布图
2 试验结果及分析
2.1 矫直前、后板形分析
通过对大生产现场进行统计,进入17辊矫直机之前的钢板浪高为30~50mm,浪距为3 000~5 000mm。模拟仿真的过程选择了更恶劣的板形,2.2m内的浪高达到了50mm。将矫直工作辊的压下量分别按照大压下工艺、小压下工艺和线性递减工艺进行调整,之后分别进行模拟。
通过分别读取3种矫直模拟过程后的ODB文件,沿矫直方向统计了钢板节点坐标后,经过坐标轴转换处理,将矫直前、后板形状况进行统计,得到的矫直前、后板形示意图如图5所示。从图中可以看出,大压下矫直工艺、小压下矫直工艺和线性递减矫直工艺都对板形的平直度有了一定的改善,其中大压下工艺矫直后残余浪高为23mm,小压下工艺矫直后残余浪高为28mm,线性递减工艺矫直后残余浪高为25mm。
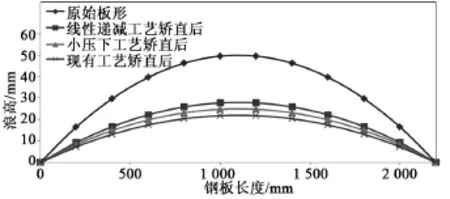
图5 各矫直工艺钢板矫直前、后板形示意图
2.2 矫直后残余应力分布分析
选择矫直后的钢板作为研究对象,研究其距离头部1 000mm处沿板宽方向的残余应力分布规律。因为钢板的长度方向尺寸要远大于宽度方向尺寸,因此沿着轧向的残余应力分布对板形的影响会更加显著。各矫直工艺矫直后的轧向残余应力分布如图6所示。
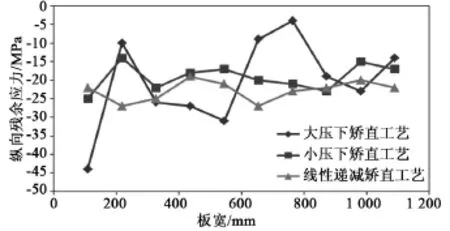
图6 各矫直工艺矫直后残余应力分布图
从图6中可以看出,当压下量很大时,矫直后钢板的纵向残余应力的数值和波动都很大。压下量降低到线性递减矫直工艺和小压下矫直工艺之后,钢板的残余应力分布更均匀。沿着板宽方向不均匀分布的纵向应力,可以导致钢板沿着矫直方向发生瓢曲。残余应力可以代表钢板的隐性板形,即可以代表钢板在矫直后再瓢曲的趋势。因此,大压下矫直工艺矫直后的钢板,其再次发生瓢曲的可能性要大于小压下矫直工艺和线性递减矫直工艺,小压下矫直工艺和线性递减矫直工艺更有利于改善钢板的隐性板形。综合矫直后显性板形和隐性板形的结果可以看出,线性递减矫直工艺矫直后的钢板的显性板形和隐性板形均较好;大压下矫直工艺矫直后虽有较好的显性板形,发生再次瓢曲的可能性仍较大;小压下矫直工艺不能很好的改善高强钢板的显性板形。
2.3 不同矫直工艺矫直力分析
选择矫直辊3作为研究对象,线性递减矫直工艺作为研究的工艺,得到矫直辊矫直力随时间的变化过程,如图7所示。从图7中可以看出,在钢板咬入矫直辊的2个过程中,矫直力较小,其余时刻矫直力基本位于800kN左右波动且较稳定。其他各辊趋势相同。

图7 矫直过程工作辊矫直力随时间变化图
对不同矫直辊的最大值进行统计,得到不同矫直工艺各矫直辊最大矫直力分布情况,如图8所示。从图8中可以看出,3种矫直方法的最大矫直力均出现在第3辊及第4辊,这与第2辊的压下量最大不符。但是考虑到初始板形的问题,初始板形是一个上翘的形状,而第2辊的最大压弯方向,正好与此方向相同,所以第2辊实际并非是最大变形的所在,而最大变形正好出现在第3辊与第4辊处,正是这种最大反弯的出现,使得最大矫直力出现在第3辊及第4辊处,其他各辊随着压下量的减少以及钢板的残余变形的减小逐渐降低。

图8 各矫直工艺最大矫直力分布示意图
从最大矫直力的数值上看,大压下矫直工艺的最大矫直力为1 160kN,线性递减矫直工艺的最大矫直力为960kN,小压下矫直工艺的最大矫直力为1 050kN。对于单个矫直辊来说,矫直力越小,越有利于保护矫直辊。计算矫直机所有矫直辊矫直力总和,大压下矫直工艺为9 740kN,线性矫直工艺为8 230kN,小压下矫直工艺为8 020kN。对于整个矫直机而言,总体矫直力越低,越有利于降低设备负荷。由此可见,线性矫直工艺的最大矫直力最低,这对于矫直机保护矫直辊有一定意义,而矫直力总和方面,线性矫直工艺和小压下矫直工艺都比大压下矫直工艺要低,这对于现场生产中矫直机矫直力不足来说有很大的借鉴意义。
3 结语
综上所述可以得出以下结论。
1)大压下矫直工艺矫直后的钢板,显性板形改善最多,其次为线性递减矫直工艺和小压下矫直工艺。
2)综合考虑钢板的显性板形和隐性板形,应当选用入口压下量11.0mm、出口压下量2.3mm的线性递减矫直工艺进行矫直。
3)把大压下矫直工艺改为线性递减矫直工艺,不仅可以保证板形良好、残余应力数值较小且分布均匀,而且矫直机的总矫直力也降低了1 510kN,有利于保护矫直机,提高生产安全性和稳定性。
[1]张春丽,杨晓臻,贺佳,等.热轧钢板矫直工艺的有限元分析[J].宝钢技术,2008(1):38-41.
[2]袁国,黄庆学,董辉,等.中厚板矫直技术发展的现状与展望[J].太原重型机械学院学报,2002(9):40-44.
[3]Jeong S H,Lee S H,Kim G B,et al.Computer simulation of U-channel for under-rail rollforming using rigid-plastic finite element methods[J].Journal of Materials Processing Technology,2008(20l):118-122.
[4]黄建国,吕昌.无缝钢管矫直分析[J].包钢科技,2007,33(2):20-22.
[5]李学通,杜风山,于凤琴.中厚板矫直过程的有限元研究[J].重型机械,2005(1):44-46.
[6]韦绍杰,廖凯,陈磊.预拉伸对铝合金淬火厚板变形的矫直仿真研究[J].热加工工艺,2013,42(9):128-130.