基于PCA-SIFT的立体匹配算法

宋淳恺

（同济大学电子与信息工程学院，上海 201804)

基于PCA-SIFT的立体匹配算法

宋淳恺

（同济大学电子与信息工程学院，上海 201804)

在双目立体视觉技术中，立体匹配算法研究是最基本的问题，SIFT算法由于对存在尺度变化等情况下的图像都能够实现图像的准确匹配而受到广泛的使用。然而，SIFT算法比较复杂，导致算法耗时效率低。为了降低算法的复杂度，满足研究对于实时性的要求，提出一种小波变换结合PCA-SIFT算法的综合的立体匹配算法。采用这种综合算法能够剔除大量图像误匹配，减少匹配计算量和时间，加快运算速度。

小波；SIFT算法；立体匹配

0 引言

双目立体视觉是图像处理领域中的热门方向，随着研究的深入，在机器人、自动驾驶等领域得到了使用，是一种从二维图像中获取三维信息的方法。它首先获取左右两幅图像的二维位置信息，再根据左右两个摄像机的参数和相对位置，按照视差原理计算图像中物体三维距离信息。双目立体视觉系统分为摄像机标定、图像矫正、立体匹配和深度计算这几个步骤，在这里面立体匹配是最关键的部分。在目前的立体匹配算法中，SIFT算法得到了广泛的使用，在现有的国内外双目立体视觉匹配算法中处于领先的地位[1]。SIFT主要优点在于其特征点尺度、旋转和光照不变性方面[2～3]明显优于其他特征描述子。但是，如果图像灰度差异大，将会导致错误的匹配。而且SIFT的算法计算量大，不适用于实时性要求较高的系统。

针对以上的问题，本文提出一种基于小波变换和PCA-SIFT算法的立体匹配算法，其目的是提高图像匹配的速度和精度。图像经过小波变换之后得到的低分辨率成分受图像局部细节的影响降低，提高了特征提取的能力和速度。而且通过阈值的设置，可以剔除匹配点对中明显的错误匹配，获得相对精确的结果。

首先通过小波分解将图像分解为低频成分和高频成分，对低频成分进行图像匹配。然后在使用SIFT算法进行匹配时，用主元分析法替换直方图法，实现描述子的降维。减少描述子维数可以提高匹配速度。最后将实验结果与SIFT结果进行对比，证明本文方法的鲁棒性和更高的效率。

1 小波分析

小波分析是继傅里叶分析后的重大突破，目前已经广泛运用于图像领域。它以傅里叶的频率变换作为基础，增加了时间上的变换，使得其可以在时间和频率上分别对信号进行局部的分析，从而使分析结果更加的有效。小波分析经过伸缩和平移的方式得到不同尺度的小波，然后利用这些不同的小波分析信号。小波分析使用时间分辨率高的小波分析频率高的信号，使用频率分辨率高的小波分析频率低的信号[4]。

小波变换基本原理如下：用基函数的加权和得到信号的近似公式，也就是用基函数来表示或者逼近信号。母小波可以通过伸缩和平移得到基础函数[5]，先将母函数缩放a倍，然后平移b：

在小波变换中，首先需要对它的两个因子进行离散化，构建规范的正交基。Haar小波是比较典型的规范正交基。Haar小波的母小波公式为：

对应的缩放函数表示为：

Haar小波速度快、维度小，可以满足算法的实时性要求，因此在这里采用Haar小波分析。在多层分析的结果中，由于从第二层开始所得到的低频分量的图像匹配点数很少，而多层分解的反复，也会增加匹配的时间。通过实验表明在小波分解的第一层可以得到正确的结果；但是在小波分解第二和第三层，由于图像小波分解使图像信息大幅度减少，会由于匹配点对不足而无法进行图像配准。因此，在本文中，仅仅使用第一层的低频分量进行匹配。

多尺度小波分解各层重建图像显示如图1所示。

图1 小波分解

2 PCA-SIFT算法

SIFT，即尺度不变特征转换，是用于图像处理领域的一种描述符。该算法通过生成一个描述符，对于特征尺度有不变性，能够在图像中计算出关键点，首先构建尺度空间找到兴趣点，接下来在兴趣点上寻找关键点，利用该点周围点的梯度方向，分配给关键点特定的方向，最后给每一个关键点设置一个矢量作为下一步匹配计算的依据，该矢量的维度为128[6～8]。具体步骤如下：

为了能更加有效地检测到关键点，将相邻尺度下的图像函数相减得到高斯差分函数，利用该函数与图像函数进行卷积，通过不同尺度的卷积乘积，最后得到一个高斯差分的相应值图像D（x，y，σ）。公式为：

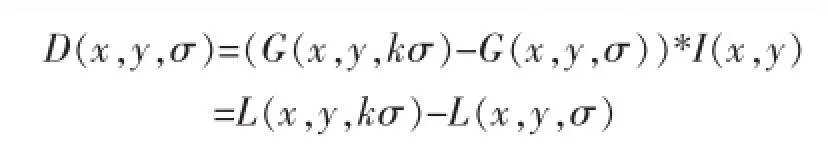
为了获得一个稳定的特征点，将不好的特征点除去，还需要删减不稳定的一部分边缘点。下式可以确定特征点的稳定性。

其中H（x，y）是Hessian矩阵。通过上一步已经可以提取出特征点在图像中的位置，接下来要给每个特征点分配一个方向，通过确定关键点周围像素点的相应梯度方向的分布特征，指定关键点的方向参数，使其具备旋转不变性。每个关键点都有其特定的尺度σ，依据这个尺度参数，可以获得最靠近该尺度值的高斯图像。把关键点作为中心，以4.5σ为半径，计算图像在这个区域中的梯度模值和方向。

m（x，y）是点（x，y）的模值，θ（x，y）是点（x，y）的方向。在关键点的梯度方向处理结果计算出来之后，接着使用直方图来统计关键点周围像素的梯度模值和方向。在整个直方图中，用横轴来表示梯度方向，用纵轴来表示该方向所对应的模值。在关键点梯度信息直方图中，把0°～360°分成36份，每10度的区域作为直方图中的一个立柱。以直方图的最大峰值作为该关键点的方向。如果同时有一个约有最大峰值80%能量的峰值存在，那么将此方向定义为该点的辅方向。通过这个步骤一个关键点可能测到不同的几个方向，这能够提高算法鲁棒性。

在SIFT算法中，为了保证特征矢量的旋转不变性，首先以特征点为中心，将坐标旋转为特征点的主方向，在每个子区域8个方向的梯度上计算直方图，通过绘制每个方向的模值形成一个种子点。一个特征点有4×4个种子点，每一个种子点的向量信息有8个方向，因此一共有4×4×8=128维。在生成两幅图像的SIFT特征向量之后，需要计算关键点的向量之间的欧氏距离，并以距离值作为关键点的相似度判定值。把第一幅图像中的一个关键点取出来，并从第二幅图像中找出其与前者欧氏距离最近的前两个关键点，找到这两个后计算它们同第一幅中关键点的欧氏距离，如果较小的值除以较大的值小于一定的百分比阈值，则为可以接受的匹配点。降低阈值虽然会减少匹配点数，但是会提高稳定性。

SIFT的尺度不变性可以减小尺度、光照和旋转对匹配的影响，提高匹配成功率，但是考虑到SIFT以下特点[9]：

（1）SIFT特征提取算法需要反复地计算平滑卷积和统计加权直方图，浮点计算极大，因而算法复杂度高、计算时间长。

（2）SIFT算法提取大量特征点，但其中只有很少一部分可以正确匹配，给未匹配成功的特征点建立描述子会占用大量时间，影响匹配和搜索速度。

这里采用改进的PCA-SIFT，在保留尺度不变性的同时降低维度，大量减少了算法运行的时间。Y.Ke和R.Sukthankar提出的PCA-SIFT，用主元分析法来替换原SIFT算法中的直方图法，实现描述子的降维[10]。主要区别在于描述子的简化：不再使用原来的4×4×8个描述子，而是以41×41的图像区域作为一个计算范围，得到数量为3042个的梯度导数，然后采用PCA方法，将之前得到的3042维方向矢量降到36维。

3 实验结果与分析

为了验证算法的有效性，将不同算法做实验比较，并对结果进行分析。在实验中对SIFT、PCA-SIFT、小波+SIFT、小波+PCA-SIFT的性能进行了对比分析。实验结果如图所示。

图2～图4为同一组图像在不同匹配算法下的效果图，图中显示的均为经过图像校正后的输出图像。左、右半部分别为左摄像机和右摄像机拍摄的图像。由以上4种匹配方法得出的性能结果统计见表1。

表1 匹配结果统计

图2 SIFT方法

图3 PCA-SIFT方法

图4 小波+SIFT方法

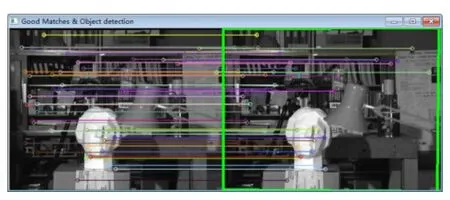
图5 小波+PCA-SIFT方法

由匹配结果可以得出，采用小波变换进行预处理后减少了匹配点数，降低了匹配复杂度，减少了算法的运行时间。综合采用小波和PCA-SIFT变换的算法在降低了特征提取和特征匹配的复杂度的同时，提高了图像特征点的正确匹配率，最终大大增强了算法的实时性。

4 结语

从上述理论分析和实验结果可以看出，基于小波和PCA-SIFT算法的方法能够满足较高精度，同时使得特征提取和匹配的复杂度大大降低，算法在实时性和准确性方面得到了显著的提高。由上述算法的分析以及实验结果对比可见:

（1）文中提出的算法采用基于PCA-SIFT的特征匹配，在保证匹配结果有效性和准确性的同时，极大提高了匹配效率和运算速度。

（2）PCA-SIFT算法在特征匹配时需要检测特征点，这一步要多次使用高斯差分函数进行运算，占据了大部分时间。文中算法为了减少特征描述生成的次数，在生成特征描述子之前先对图片进行小波分解，使得该阶段的计算量大大减少，迅速提高了实时性。小波+ PCA-SIFT算法生成的特征点个数远远少于SIFT算法，从而使匹配特征点数大量减少，缩短了匹配的时间。

[1] 潘华，郭戈.立体视觉研究的进展[J].计算机测量与控制，2004，12（12）：1121～1124

[2] DG，L..Distinctive Image Features from Scale-Invariant Keypoints[J]，2004，60（2）:91～110

[3] K.，M.，S.C..A Performance Evaluation of Local Descriptors[C].2005，27（10）:1615～1630

[4] 孙延奎.小波分析及其应用[J]，2004:199～205

[5] 宋国乡，冯象初，甘小冰.数值泛函与小波理论[J]，2003:西安电子科技出版社

[6] 宰小涛，赵宇明.基于SIFT特征描述子的立体匹配算法[C].微计算机信息，2007，23（24）：285～287

[7] Lowe，D.G.，I.O.E.A.Engineer.Object Recognition from Local Scale-Invariant Features[M].in Computer Vision，1999.The Proceedings of the Seventh IEEE International Conference on vol.2.1999

[8] Cong，Y.，X.Chen，Y.Li.Research on the SIFTAlgorithm in Image Matching[C].in ICFMD2011.2011.Taiwan，China

[9] 赵钦君，赵东标，韦虎.Harris-SIFT算法及其在双目立体视觉中的应用[J].电子科技大学学报，2010，39（4）：546～550

[10] R，Y.K.S.A More Distinctive Representation for Local Image Descriptors[J].in IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2004.Washington，USA

Stereo Matching Algorithm Based on PCA-SIFT

SONG Chun-kai
（School of Electronics and Information Engineering，Tongji University，Shanghai 201804）

In binocular stereo vision technology,stereomatching algorithm research is themost basic problem,SIFT algorithm has been widely used due to be able to achieve the accuracy of the image matching in circumstances such as changing the existing scale of image.However, SIFT computation is too complex so it leads to a long time,and the efficiency is low.In order to reduce the complexity of the algorithm to achieve real-time requirements in research,proposes a combination of wavelet transform and PCA-SIFT stereo matching algorithm. Adopting this integrated algorithm can eliminate a large number of image matching errors,reduce the matching computation,shorten matching time,speed up the operation.

Wavelet;SIFTA lgorithm;Stereo Matching

1007-1423（2015）06-0031-05

10.3969/j.issn.1007-1423.2015.06.007

宋淳恺（1989-），男，浙江慈溪人，在读硕士研究生，研究方向为图像处理立体视觉领域

2015-01-08

2015-01-20