SVM方法在模式识别应用领域中的发展与研究

朱亚辉，黄襄念

（西华大学数学与计算机学院，成都 610039）

SVM方法在模式识别应用领域中的发展与研究

朱亚辉，黄襄念

（西华大学数学与计算机学院，成都 610039）

SVM是一种新型机器学习方法。对SVM训练算法的最新研究成果进行综述，并且介绍目前研究的新进展，总结SVM在模式识别中的应用现状以及对其发展趋势进行展望。

SVM；模式识别；机器学习；数据挖掘；模式分类

0 引言

SVM方法是学习的泛化能力的体现，SVM借助最优化方法，解决小样本、高维数、非线性和局部最小点等实际问题上表现非常出色，并有效解决了模式分类、维数灾难和过学习等问题。它具有较好的推广能力、泛化能力和全局最优性能，以及出色学习能力，成功地解决了模式识别中很多问题，并得到了广泛的应用。学术界普遍认为它是继神经网络之后，在大数据时代一个新的研究方向，使机器学习进入了一个新的时期。

1 SVM方法的发展与研究现状

SVM方法是基于统计学理论VC维理论和结构风险最小原理基础上的机器学习方法，SVM理论基础决定了它最终求得的是全局最优值而不是局部极小值，提高对未知样本的良好泛化能力。其良好的优化性能，普遍受到更多研究人员的重视。目前，在算法改进和理论研究取得了重大突破，现在已成为模式识别领域中研究的热点。

1.1 SVM方法的原理

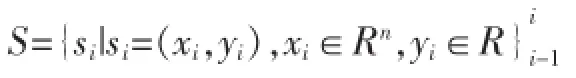
近年来，对SVM的研究主要集中在其本身性质的研究和以及加大SVM应用研究的深度和广度。

1.2 SVM训练算法

（1）块算法和分解算法

从最早1995年Cortes和Vapnik提出了块算法（Chunking Algorithm）[3]，在1997年由Osuan等人提出并应用于人脸检测的分解算法[4]。Joachims基于分解算法做出了重要改进，提出了Shrinking方法。为了提高运算和收敛速度，1998年，Platt提出了顺序最小优化算法[5]。Joachim从工作集角度提出了SVMlight算法[6]，它是Osuan分解算法的一种推广，实现了基于此算法的软件包SVMlight。

（2）变形算法

变形算法主要是通过增加函数项、变量或系数等方法使公式变形，产生出各种有某一方面优势或者一定应用范围的算法。

Suykens等人提出了最小二乘SVM[7]（Least Squares SVM，LS-SVM），使SVM的训练等价于一组线性方程组的求解。对支持向量稀疏性进行了改进，提出了回归问题的稀疏近似策略。在LS-SVM的基础上，又提出了如动态加权LS-SVM等改进算法。针对二次规划无约束对偶问题，提出了Huber近似算法[8]、多拉格朗日乘子协同优化算法。

（3）几何方法

SVM方法的几何意义主要体现在训练样本的结构和空间距离的重定义。文献[12]提出了一种直观的几何方法来选择大数据的SVM训练，时间复杂度是线性的训练集大小为n的特征空间凸包样本。文献[13]为SVM分类问题的几何框架提供了一个直观地用于理解和几何优化算法的应用。文献[14]提出了基于压缩凸包的SVM分类问题的几何算法，保持了数据的几何体形状，并且易于得到确定其极点的充要条件。文献[15]提出了一种SK类思路SVM的几何方法，该类算法迭代过程中，其最优点多在顶点和边界上，并在第一次迭代就可能达到边界。

（4）增量算法

增量学习是处理机器学习中与新样本有关的部分进行增加、修改或删除等操作过程，增量训练算法的特点是一次反复优化的过程。

Ahmed.S.N最早提出了SVM增量训练算法[16]，选择一小批常规二次规划算法作为增量，使支持向量和新增样本进行混合训练。文献[17]针对经典SVM难以快速有效地进行增量学习的缺点，提出了基于KKT条件与壳向量的增量学习算法，该算法选择包含所有支持向量的壳向量，利用KKT条件淘汰新增样本中无用样本，减少参与训练的样本数目，在新的训练集中快速训练SVM进行增量学习。文献[18]针对支持向量回归因时空复杂度较高而无法处理大规模数据的问题，提出了一个新的回归增量学习法。文献[19]为了解决SVM在增量学习时，由于支持向量选择不完全，导致增量学习过程无法持久进行的问题，提出了最大似然边界SVM增量学习算法。

（5）多类分类算法

SVM两类分类器扩展到多类分类问题上，需要构造多类SVM分类器，其构造方法有多种，其中典型的是组合多个两类分类器，包括：一对多算法、一对一算法和决策导向无环图，其次是SVM决策树方法。

文献[20]提出了一种改进的基于二叉树结构的SVM多类分类算法，有效地解决现有SVM多类分类算法的不可分区域问题及提高了泛化能力。文献[21]提出了一种基于样本的类划分方案，采用平衡决策树的结构，得到一种新的决策树SVM多类分类算法，有效地减少了样本训练时间，提高了多类分类器的识别率。文献[22]提出了一种基于对SVM的多类分类算法，有效地处理大规模数据时训练速度上存在的弱势。

（6）模糊SVM

模糊SVM是如何给训练样本确定相应权重，使不同的样本对决策函数的学习做出不同的贡献，可以减少对外部的影响。

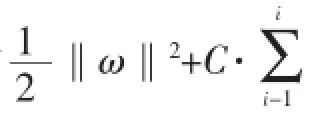
（7）粒度SVM

粒度SVM主要的研究是内在学习机制，在SVM学习框架下，引入粒与粒的内积运算，建立粒度核函数并将之运用于粒度SVM的学习之中。

文献[27]通过引入动态层次粒度的方法，设计了动态粒度SVM回归模型。文献[28]针对数据规模和分布密度不平衡的数据集，提出了一种基于粒度偏移因子的粒度SVM学习方法，是将原始样本用Mercer核映射到高维空间，对数据进行有效的粒划分，重新构造SVM的凸二次优化问题，以得到一个泛化能力更好的分类超平面。文献[29]提出一种动态粒度SVM学习算法，根据粒的不同分布自动粒划分，使SVM可在不同层次的粒上训练，结果具有更好的分类性能。

（8）孪生SVM

孪生SVM是一种二值数据的分类器，求解两个二次规划问题的一种快速分类方法，具有很强的数据处理能力。文献[30]提出了模糊加权孪生支持向量机，通过为每个训练样本赋予不同的样本重要性，以及减少样本点对非平行超平面的影响。文献[31]是对文献[30]的改进，提出了加权光滑CHKS孪生SVM。文献[32]提出了一种广泛权重的最小二乘孪生SVM新型模式分类器，该SVM在正、负两类样本上广泛地增加权重，很好地抑制了交叉噪声样本对数据分类的影响。文献[33]提出了基于孪生SVM的特征选择与分类算法研究，从流形学习和聚类技术两方面对孪生SVM进行改进，求解两个SVM的二次规划问题来获得分类模型，从而缩短了训练时间。

（9）排序SVM

排序学习是当前机器学习研究的热点，现有排序学习算法把训练样本广泛应用于回归和分类的学习。文献[34]提出了一种基于有监督学习的融合多个与查询相关排序子模型的方法，使用子排序模型的输出进行向量化表示，将多个查询相关的排序模型转化为特征数据，实现多排序模型的集成。文献[35]提出了一种基于距离排序的快速SVM分类算法，计算两类样本点的样本中心距离，选择比例的小距离样本作为边界样本。文献[36]将视觉目标跟踪问题视为一个排序学习问题，利用排序SVM进行目标跟踪，提出了两种新的目标跟踪算法，并且应用于日益受到重视的红外视频下的目标跟踪问题，实现对红外视频目标的鲁棒性跟踪。

2 SVM方法在模式识别中的应用

SVM方法由于其在理论上具有全局最优、良好的推广能力，在很多问题上有其他统计学习技术难以比拟的优越性，近几年，许多关于SVM方法的改进与应用的研究，对国内外学术界产生了巨大影响。

随着对SVM研究的不断深入，并且SVM方法有着突出的优势，它能够保证找到极值解，即全局最优解而非局部最小值，这也就决定了SVM方法对未知样本有较好的泛化能力。正由于这些优点，SVM的一些模型和方法在各种应用领域表现出较好的推广能力，得到了广泛的应用，在模式识别领域的应用最为普遍，如人脸检测与人脸识别、手写数字识别、文本分类、说话人语音识别、图像识别、图像分类与检索等，已成功解决了许多模式识别问题。

3 SVM方法的发展趋势与展望

SVM理论研究与实际应用研究之间还存在较大差距，许多问题的研究需要更一步的扩展和学习，需要不断深入统计学理论的研究，加快SVM算法发展。目前，下述几个方面的问题值得进行深入研究：

（1）如何扩展SVM算法本身推广性能的核函数及其参数，选择简单、高效、实用的核参数将是未来研究的关键。

（2）如何提高在SVM应用中求解问题的速度和规模。线性SVM结合自身特点，将能够设计出更好的训练算法，处理大规模数据的快速算法，将是今后重点关注的问题。

（3）如何有效地将二类别分类器扩展到多类别问题上，仍是今后研究的重点。还将扩大对回归问题、对聚类和时间序列分析问题的研究。

（4）如何提高特征提取的质量，获取好的分类基础，完善SVM在实际应用中的性能。不断提高SVM训练速度，构造高效的训练算法，加大对SVM理论与具体算法实现的研究。

[1] 崔和，龙玉峰.支持向量机学习算法的研究现状与展望[J].信息与电子工程，2008，09（1）：328～331

[2] 丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报，2011，40（1）：3～10

[3] Baser B，Guyton I，Vapnik V.A Training Algorithm for Optimal Margin Classifiers[C].M Proceedings of the 5th Annual ACMWorkshop on Computational Learning Theory.New York:ACM Press，1992：144～152

[4] Osuna E，Frenud R，Girosi F.An Improved Training Algorithm for Support Vector Machines[C].M Proceedings of IEEEWorkshop on Neural Networks for Signal Processing.New York，USA，1997：276～285

[5] Platt J.Fast Training of Support Vector Machines Using SequentialMinimal Optimization[M].MA.J.Smola，B.Scholkopf，C.Burges，eds.Advances in Kernel Methods:Support Vector Machines，Cambridge，MA:MIT Press，1999：185～208

[6] Joachim T.Making Large-Scale SVM Learning Practical[A].Burges C，Scholkopf B.Advances in KernelMethods:Support Vector Learning[C].Cambridge，MA:MIT Press，1998：169～184

[7] Suykens JAK，Vandewalle J.Least Squares Support Vector Machine Classifiers[J].Neural Processing Letters，1999，9（3）：293～300

[8] 周水生，詹海生，周利华.训练支持向量机的Huber近似算法[J].计算机学报，2005，28（10）:1664～1670

[9] Keerthi SS，Shevade SK，Bhattacharyya C，etal.A Fast Iterative Nearest Point Algorithm for Support Vector Machine Classifier Design[J].IEEE Transactions on Neural Networks，2000，11（1）:124～136

[10] Scholkopf B，Smola A，Williamson R C，et al.New Support Vector Algorithms[J].Neural Computation，2000，12（5）:1207～1245

[11] Chang Chih-Chung，Lin Chih-Jen.Training V–Support Vector Classifiers:Theory and Algorithms[J].Neural Computation，2001，13（9）:2119-2147.

[12] Zhi-Qiang Zeng.A Geometric Approach to Train SVM on Very Large Data Sets[C].Intelligent System and Knowledge Engineering，2008.ISKE 2008.3rd International Conference on Xiamen，2008，17～19（8）：991～996

[13] Mavroforakis，M.E.A Geometric Approach to Support Vector Machine（SVM）Classification[J].IEEE Computational Intelligence Society IEEE Computational Intelligence Society，2006，08（5）：671～682

[14] 彭新俊，王翼飞.基于CCH的SVM几何算法及其应用[J].应用数学与力学，2009，15（01）:90～100

[15] 常振华，陈伯成，李英杰，刘文煌，闫学为.SVM的几何方法——SK类思路的研究[J].计算机工程与应用，2011，11（03）:149～153

[16] Liefeng Bo，LingWang，Licheng Jiao，Training Hard Margin Support Vector Machine Using Greedy StageWise A lgorithm，Lecture Notes in Computer Science（PAK DD2005），2005，3518：632～638，2005

[17] 文波，单甘霖，段修生.基于KKT条件与壳向量的增量学习算法研究[J].计算机科学，2013，40（3）:255～258

[18] 张一凡，冯爱民，张正林.支持向量回归增量学习[J].计算机科学，2014，41（6）:166～170

[19] 曹健，孙世宇，段修生，张泽建.基于KKT条件的SVM增量学习算法[J].火力与指挥控制，2014，15（7）:139～143

[20] 刘健，刘忠，熊鹰.改进的二叉树支持向量机多类分类算法研究[J].计算机工程与应用，2010，33（11）:117～120

[21] 刁智华，赵春江，郭新宇，陆声链.一种新的基于平衡决策树的SVM多类分类算法[J].控制与决策，2011，26（01）:149～152

[22] 聂盼盼，臧洌，刘雷雷.基于对支持向量机的多类分类算法在入侵检测中的应用[J].计算机应用，2013，33（2）:426～429

[23] 丁胜锋，孙劲光.基于混合模糊隶属度的模糊双支持向量机研究[J].计算机应用研究，2012，10（10）:432～435

[24] 徐国浪，魏延.基于多核函数的模糊支持向量机学习算法[J].重庆师范大学学报，2012，29（6）:50`53

[25] 李凯，卢霄霞.种基于粗糙间隔的模糊支持向量机[J].电子学报，2013，41（6）:1183～1187

[26] 曹建芳，焦莉娟.基于模糊支持向量机的图像分类方法[J].计算机与数字工程，2013，41（4）:638～641

[27] 郭虎升，王文剑.动态粒度支持向量回归机[J].软件学报，2013，15（11）:2535～2547

[28] 郭虎升，王文剑.基于粒度偏移因子的支持向量机学习方法[J].计算机研究与发展，2013，15（11）:2315～2324

[29]程凤伟，王文剑，郭虎升.动态粒度SVM学习算法[J].模式识别与人工智能，2014，15（4）:372～377

[30] 李凯，李娜，卢霄霞.一种模糊加权的孪生支持向量机算法[J].计算机工程与应用，2011，14（11）:162～165

[31] 丁世飞，黄华娟，史忠植.加权光滑CHKS孪生支持向量机[J].软件学报，2013，15（11）:2548～2557

[32] 储茂祥，王安娜，巩荣芬.一种改进的最小二乘孪生支持向量机分类算法[J].电子学报，2014，26（05）：998～1003

[33] 封瑞.基于孪生支持向量机的特征选择与分类算法研究[D].西安电子科技大学，2013，10（1）：1～29

[34] 王扬，黄亚楼，谢茂强，刘杰，卢敏，廖振.多查询相关的排序支持向量机融合算法[J].计算机研究与发展，2011，48（4）:558～566

[35] 胡志军，王鸿斌，张惠斌.基于距离排序的快速支持向量机分类算法[J].计算机应用与软件，2013，30（4）:593～597

[36] 刘锴.基于排序支持向量机的目标跟踪算法研究[D]，厦门大学，2014，01（4）:5～19

Development and Research on the SVM Methods in the Field of Pattern Recognition App lications

ZHU Ya-hui，HUANG Xiang-nian
（School ofMathematics and Computer Engineering，Xihua University，Chengdu 610039）

Support Vector Machines is a new typemachine learningmethod in recent years.Reviews the latest research results on the training algorithms of SVM，and introduces new progress of the present study，summarizes the SVM application status in pattern recognition aswell as the prospects for its development trend.

SVM;PatternRecognition;Machine Learning;Data Mining;Pattern Classification

1007-1423（2015）06-0020-05

10.3969/j.issn.1007-1423.2015.06.005

朱亚辉（1989-），男，河南商丘人，硕士，研究方向为图像处理与模式识别

黄襄念（1965-），男，四川成都人，教授，博士，研究方向为图像处理与模式识别、体感交互技术与虚拟现实

2014-09-23

2015-01-28