网格尺寸对Delft3D有限元水流场仿真精度影响的分析

张仁徽，陈宇里，耿钊

上海海事大学商船学院，上海 201306

网格尺寸对Delft3D有限元水流场仿真精度影响的分析

张仁徽，陈宇里，耿钊

上海海事大学商船学院，上海 201306

针对有限元水流场仿真中有效地选择网格尺寸、平衡计算精度和计算成本的问题，采用在网格形状、边界激励类型、边界激励量大小等因素相同的条件下，输入不同的网格尺寸分析了仿真的精度误差的方法，建立了海南某港的Delft3D-FLOW模块水流场仿真模型。研究结果表明：仿真计算的绝对误差基本呈非线性关系，相同条件下靠近岸线的位置仿真误差大于海域中间的位置仿真误差。

有限元；水流场；网格尺寸；精度分析；Delft3D

随着计算技术的发展，使用有限元方法对海洋流场仿真已经成为一种实用的研究手段。对水流场的仿真经历了从二维到三维的发展阶段，目前三维模式应用已经比较普遍，可以通过专业软件的仿真更精确地反映出潮流的运动规律。水流场的精确仿真不仅是溢油模拟、海洋生态模拟等研究的基础，更能为深水港、跨海大桥、航道治理等工程建设，货运船舶及军舰的操作提供参考数据。

一般设想中，有限元仿真模拟使用的网格越精密其计算结果产生的误差就越小，同时也带来了更大规模的计算量，需要更多的计算时间。然而实际操作中，由于计算机数据字长及对其舍入的作用，部分误差反而会因为网格单元划分过小而累积。因此在实际的工程运用中，使用多大尺寸的网格能获得计算精度、计算效率和技术成本的最好平衡，就成了技术人员面对的一个难题。针对这一问题，本文对具体案例进行水流场模拟，通过比对不同尺寸的网格得出的计算结果，对网格单元的划分与计算精度的关系进行探讨。

1 基本原理

1.1 Delft3D模型

Delft3D水动力学模型是由荷兰水利研究所开发的一款水动力学模型，可以在二维或三维层面通过有限元单元法对水流场进行仿真。该仿真系统大致包含6个某块：水流、水动力、波浪、泥沙、水质、生态等，在国内外都有广阔的运用领域。我国从20世纪80年代中期就已经开始将该系统运用于相关项目，如长江口、长江重庆城区段、杭州湾、渤海湾、滇池、辽河、三江平原等，都相继取得了不错的效果。

文中的模拟实验主要使用的是Delft3D中的FLOW模块（水动力模块）。FLOW模块的主要功能是模拟众多不同的水流条件，如湖泊和大洋中的风生流、河口及入海口的潮汐流和实验水槽中的紊流等等。FLOW模块能够建立不同规模的直线或曲线网格来计算非稳定流，并且其在计算中提供了丰富的开边界条件和初始条件，如不同来源的水流流速、流量、糙率或是天文潮等，可以模拟风对水体表面的作用，甚至能在每一个网格点上设置独立的水深数据。可以说，FLOW模块是Delft3D系统的一个核心模块。

1.2 FLOW模块的计算原理

FLOW模块建立在Navier-Stokes方程的基础上，采用有限差分法中交替隐式法（ADI）对相应坐标系下的控制方程组进行离散求解。忽略在垂直方向动量方程中垂直加速度的影响，进而推导出静水压强假定下的水流方程。

本文的仿真计算中，主要涉及两组方程（连续方程与动量守恒方程）与边界条件表达式。

1.2.1 模型控制方程

波动方程（Cartesian坐标系）：

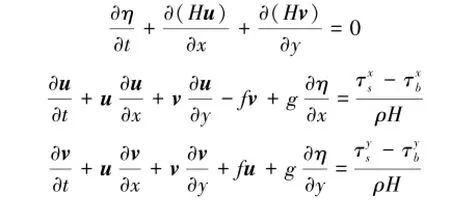
式中：η为平均海平面以上的水位，m；H为总水深，H＝h＋η，m；u、v为深度平均速度的东分量和北分量，m／s；x、y为空间坐标，m；t为时间坐标，s；h为净水深，m；f为Coriolis参数，1／s；g为重力加速度，m／s2；为风应力分量；为底应力分量。

式中：C为Chezy系数，C＝nH／6，其中n为Manning系数；ρ为海水密度，kg／m3。

1.2.2 界条件和初始条件

潮波计算采用下列边界条件。沿闭边界（水陆边界）垂直海岸的流通量等于零：

Vn＝0

式中：V＝（u，v），n是指向边界外的单位法向量。

关于对流项，在开边界当海水向计算区域流进时，法向流速的导数等于零。

2 仿真过程及分析

2.1 案例介绍

本文所模拟的水流场为海南省西南部某港，东经108°56′30″～109°48′28″，北纬18°09′34″～18°37′27″。该水域属不正规日潮混合潮型，以日潮为主，且有明显的日潮不等现象。根据该港波浪观测报告，本区潮流具有往复流特征，流向大都集中在290°～350°和120°～180°之间。大潮流速明显大于小潮流速。大潮最大流速为0.76 m／s，小潮最大流速为0.42 m／s；大潮最大垂线平均流速为0.67 m／s，小潮最大垂线平均流速为0.32 m／s。受风、浪及地形等影响，本区亦有余流存在，但流速较小，一般在8～10 cm／s。

2.2 物理参数

由于地理结构的变化，不同算例中的物理参数和边界条件都不尽相同。为有效控制仿真计算的稳定性，本文通过查阅大量文献，在仿真中将相关物理参数设定如表1所示。

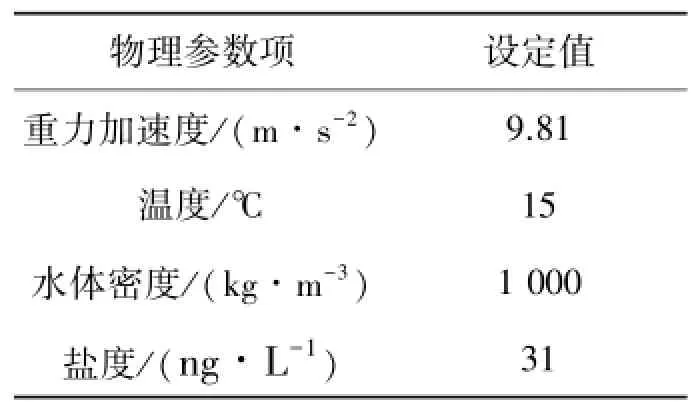
表1 物理参数值的设定

本文选用的仿真模型在数值计算上使用流体表征粘性影响系数为chezy系数，在本案例中chezy值恒为65。水平涡流黏度为1㎡／s。

2.3 网格形状的选择

有限元仿真常用的网格有二维三角形，二维四边形和三维四面体元、五面体元和六面体元。他们的边界形状主要有直线型、曲线型和曲面型。单元最佳形状是正多边形或正多面体，其具有良好相容性、逼近精确性和剖分过渡性和自适应性，单元之间过渡相对平稳。以二维三角形和二维四边形为例，相关文献表明，在步长基本相同的情况下，四边形网格的计算时间、解的精度等方面均优于三角形网格，尤其是收敛速度方面，明显优于三角形网格。

本文所选的有限元仿真模型所使用的网格即为二维四边形网格，能够较好地满足计算稳定性和精度的要求。

2.4 网格规模的确定

在仿真中，不合适的网格规模将影响网格的正交性，甚至引起边界网格发生畸变，直接影响仿真的计算精度和计算用时。对此，本文所选用的仿真模型对网格正交性的最低要求为：cosϕ＜0.02，ϕ为网格横纵方向的夹角。

本文案例中仿真的水域面积约为50 000平方公里，通过实验表明，当网格尺寸小于2 000，即网格长度小于0.6 km时，网格的正交性才能满足cosϕ＜0.02。因此本文选用的网格尺寸，最大为2 000。

2.5 仿真过程

本文在对选定水域进行仿真使用的开边界初始条件中的主要激励，为对该水域产生影响最大的4个主要天文分潮：O1、K1、S2、M2。4个天文分潮的振幅、迟角的数据由潮汐表上潮汐调和常数求得。具体数值为M2分潮振幅0.2，迟角345°；S2分潮振幅0.07，迟角70°；O1分潮振幅0.3，迟角295°；K1分潮振幅0.3，迟角345°。

为便于比较不同网格计算精度，本文以精度输出和预估计算量为考量标准，采用了若干种不同疏密程度网格模型。全部尺寸的网格采用的都是均匀网格。为研究精度较大时网格尺寸改变带来的误差变化坡度，在500以前网格尺寸以100为单位减小，500以后网格尺寸以倍数减小。网格尺寸的具体参数见表2。

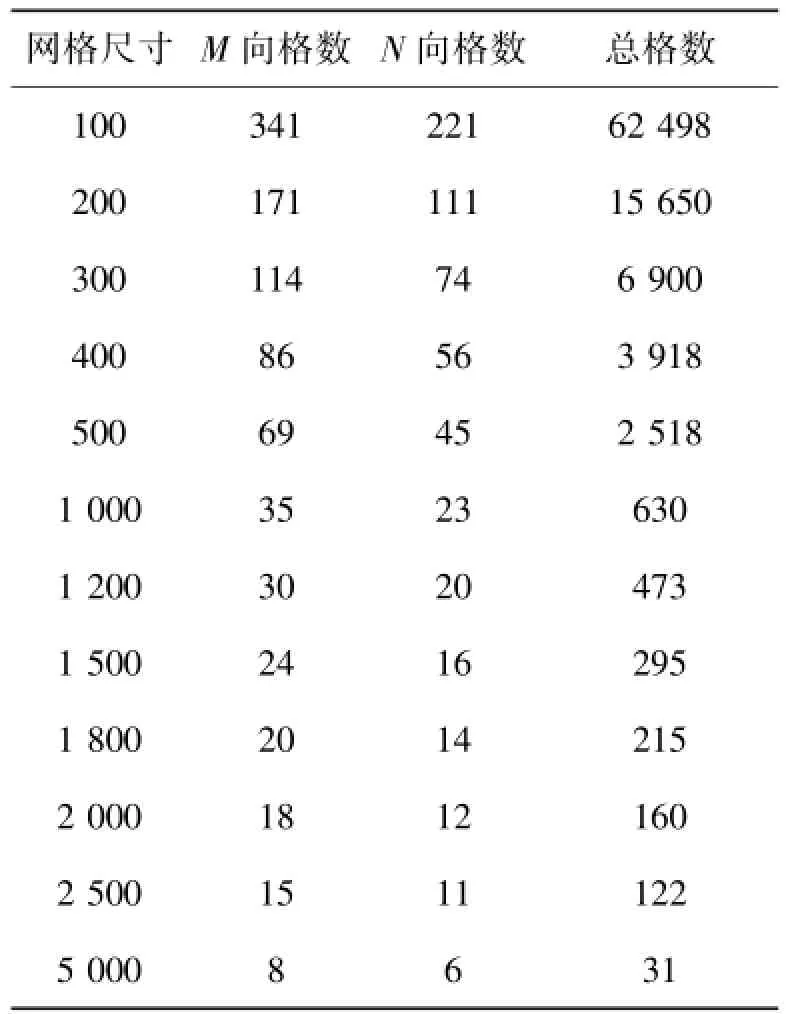
表2 网格尺寸参数

为确保网格边界的计算畸变不影响计算结果，在建立网格时尽可能包含附近较长的海岸线，并且在保证靠近边界的网格正交性的前提下使其尽可能与岸线贴合。

在模拟中，本文共选取了3个测点：测点1靠近海岸，测点2在海域中间，测点3在远离输入激励的边界。如图1所示。

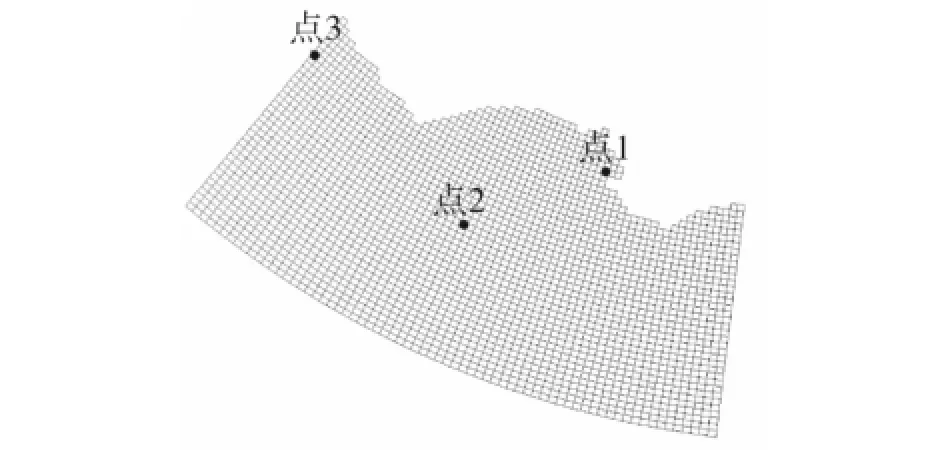
图1 仿真中3个观测点的位置

建立网格模型和输入边界激励条件后，在工程机上运行Delft3D的FLOW模块进行有限元仿真计算，设定的仿真时间段为30 d。在经过一段时间的激励输入后，可得较为稳定的仿真状态。同时可以输出海域中每个网络节点的即时潮流全息数据（流速、流向等）。图2为观测点1在状态稳定后某一天24 h之内的潮流信息。

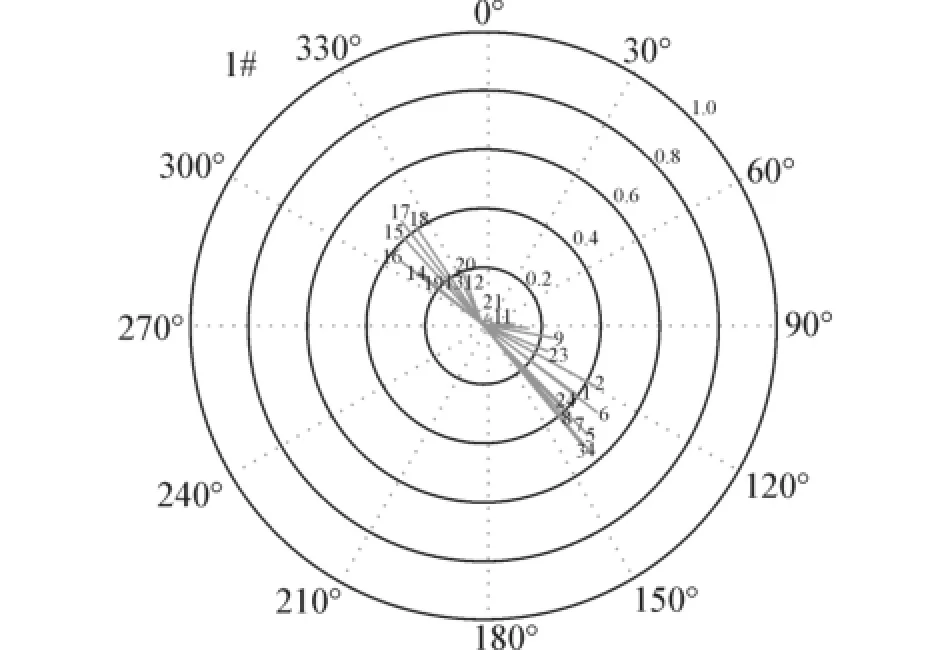
图2 观测点1在1 d内的潮流信息

在输出的观测点数据中选取13 d，每天24 h的模拟稳定潮流信息。可得到3个观测点在激励条件和仿真时间相同的情况下，使用不同尺寸的网格仿真计算出的节点流速和流向。

本文以观测站的实际观测资料作为标准数据，将不同网格尺寸的数据与实际测量值对比，分别计算它们的相对误差，并对所有误差进行横向分析。

图3 观测点2在100×100网格条件下的潮流信息对比

验证资料取用2010年6月10日～6月11日（大潮）的水文测量资料，对大潮的潮位过程进行潮位验证。流速验证取用3个测点的垂线平均流速值。分别将3个观测点各种网格精度下的仿真计算结果与真实观测值进行比对。图3为观测点2在网格精度为100×100条件下的矢量对比图。

依次将3个观测点的仿真流向和流速与观测值进行对比，得到仿真计算精度误差变化。图4由上至下依次为不同尺寸的网格模型在3个观测点的流向和流速计算精度误差变化。

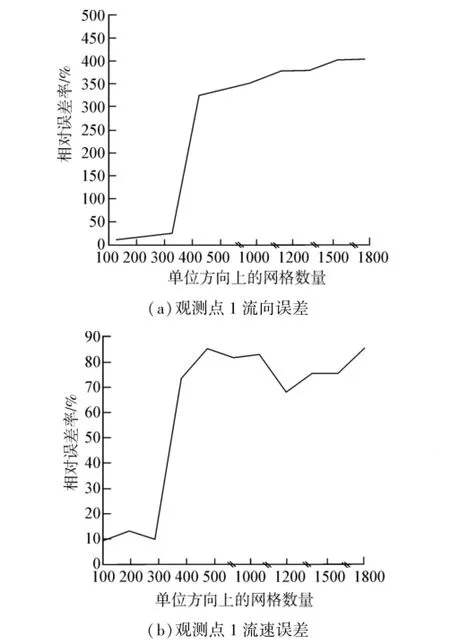
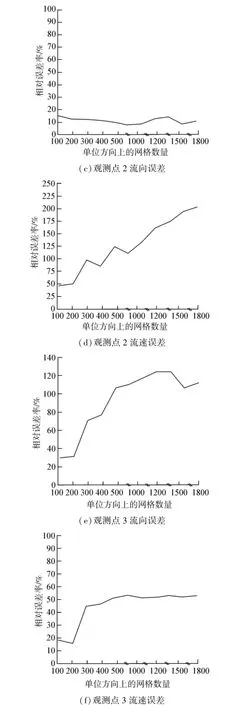
图4 观测点计算精度误差变化趋势

2.6 仿真结果分析

由图4可以看出，在FLOW模块的仿真中，总体趋势上尺寸越精细，仿真计算值与观测值接近度越高，网格尺寸越大，绝对误差也呈增大趋势。可见在仿真中由计算机数据步长和取舍造成的累积误差并不明显。

在网格尺寸由100到500增大的过程中，误差曲线较为陡峭，误差的上升速度相对较快。而在网格尺寸到达500以后，虽然尺寸增大的速度增加了，误差曲线却趋于平缓，误差的增速趋于稳定。

对比3个不同的观测点，在网格尺寸相同的条件下，由于所处位置的不同，输入的仿真数据误差量也有着较大区别。以水流速度误差为例，可以看到靠近岸线的观测点1的最大误差超过了300%，远离初始边界的观测点3最大误差也达到120%，而处于仿真海域中间位置的观测点2即使在网格尺寸相当大的情况下，仿真计算误差仍然没有超过20%，并且增长曲线非常平缓。这是由于靠近岸线的观测点所处的网格需要贴合岸线的曲线，当网格尺寸变大的时候，会导致边界网格的正交性变差、不平滑，甚至出现畸变的情况，而远离激励输入的初始边界的观测点所处位置受到激励驱动所达到的状态不够稳定，这都是导致仿真误差增大的原因。

图5 同一观测点不同网格尺寸下的流速仿真值

由图5可以看到，对于同一个观测点，随着网格尺寸的增大，仿真模拟的稳定性也大大降低。在实际仿真输出中，常取某个时刻的数值作为参考，因为稳定性的下降直接导致仿真误差的加剧。而在网格尺寸等仿真条件相同时，某点仿真流速和流向的输出误差值，基本处于同一数量级，没有明显差异。

3 结束语

通过对仿真结果的精度进行比较，工程技术人员在使用FLOW进行水流场模拟的时候，若工程对象为码头、溢油模拟等靠近岸线的内容，则应选用较为精细的网格；若工程对象为在海域当中，如为模拟船舶操纵而进行水流场仿真等，可以适当考虑使用较粗糙的网格，以在可接受的误差范围内节省仿真时间和仿真成本。

研究结果表明，相同条件下靠近岸线的位置仿真误差误差曲线较为陡峭，误差的上升速度相对较快；海域中间的位置仿真误差增长曲线非常平缓。

本次研究在相同的水文条件下，重点关注不同网格尺寸对于精度误差的影响，在今后的研究中可以更多分析不同形状的网格对于仿真精度的影响，以及不同形状的网格适用于何种工程仿真之中。

［1］徐腾飞，赵人达.计算机精度对随机场网格尺寸的影响［J］.计算机工程与应用，2011，47（17）：210-211.

［2］陈荣昌，赵前，邓健，等.Delft3D和Oilmap在内河溢油模拟中的联合应用研究［J］.中国水运，2011，11（4）：65-67.

［3］杨益洪.西湖混合流三维数值模拟研究［D］.杭州：浙江大学，2007：24-36.

［4］修荣荣，徐海明，黄善波.网格单元形状对数值计算的影响［J］.工程热物理学报，2004，25（2）：317-319.

［5］郭军朝，谷正气，孟庆超.基于湍流模型在轿车底部流场的仿真分析［J］.计算机仿真，2007，24（4）：258-261.

［6］龚曙光，谢桂兰，邱爱红，等.CAE仿真分析中计算精度与网格划分关系的探讨［J］.设计与研究，2008，21（12）：35-38.

［7］秦权，林道锦，梅刚.结构可靠度随机有限理论及工程应用［M］.北京：清华大学出版社，2006：78-92.

［8］史恒通，王成华.土坡有限元稳定分析若干问题探讨［J］.岩土力学，2000，21（2）：152-155.

［9］裴利剑，苏莲萍，张玮，等.网格疏密和模型边界对强度折减法计算精度的影响［J］.昆明冶金高等专科学校学报，2010，26（5）：64-68.

［10］裴利剑，姚永仲.边坡稳定有限元中泊松比的影响［J］.昆明冶金高等专科学校学报，2009，25（3）：56-59.

［11］ZHANG J，ELLINGWOOD B.Orthogonal series expansions of random fields in reliability analysis［J］.Journal of Engi-neering Mechanics，1993，120（12）：2660-2677.

［12］MCCAY D F.Development and application of damage as-sessmentmodeling：examp le assessment for the North Cape oil spill［J］.Marine Pollution Bulletin，2003，47（9／10／11／12）：341-359.

Influence analysis of themesh size on the precision of flow field simulation of the the Delft3D finite element

ZHANG Renhui，CHEN Yuli，GENG Zhao
Merchant Marine College，Shanghai Maritime University，Shanghai201306，China

：In order to select themesh size efficiently，and balance the calculation precision and computational ex-pense in the simulation of finite element flow field，a Delft3D-FLOW field simulation model at a portof Hainan was established.The precision error of the simulation was analyzed by inputting variousmesh sizes with constantmesh shapes，types and values of boundary incentive.The analysis result shows that，the absolute simulation errors are non-linear，and the simulation error near the shoreline is greater than that in themiddle of the ocean area under the same simulation conditions.

finite element；flow field；mesh size；precision analysis；Delft3D

TB115

：A

：1009-671X（2015）01-057-05

10.3969／j.issn.1009-671X.201402003

http：//www.cnki.net／kcms／detail／23.1191.U.20150112.1530.005.htm l

2014-02-24.

日期：2015-01-12.

交通运输部应用基础研究基金资助项目（2013329810300）；上海市教委科研创新基金资助重点项目（13ZZ124）.

张仁徽（1989-），男，硕士研究生；陈宇里（1979-）男，副教授，博士.

张仁徽，E-mail：306852381＠qq.com.