二维Hilbert曲线构造与绘制
施志林
摘 要:Hilbert是一种经典的空间填充曲线,具有严格的自相似性,可以将他划分成一些很小的单元,只是方向不一。且具有良好的空间聚集特性,应用也很广泛,譬如在图像置乱加密,数据压缩,数据索引编码等。Hilbert曲线比其他的填充曲线如Z-Ordering、Gray更能保持原始数据的性能。因此详细了解Hilbert曲线原理并使用一种自己熟悉的计算机语言来绘制Hilbert有很大的意义。因此,该文主要介绍二维Hilbert曲线的构造及原理并用C#编程语言将它实现。
关键词:Hilbert曲线 递归 自相似
中图分类号:G64 文献标识码:A 文章编号:1674-098X(2015)01(c)-0217-01
Hilbert曲线是由德国数学家David Hilbert发现的一种可以填满整个正方形的分形曲线。当阶数达到一定程度的时候,这条曲线可以填满整个正方形。目前被应用于很多方面,如图像置乱,数据加密,数据压缩等且效果不错。Hilbert曲线也具有很好的聚集效果,当给每个端点按顺序编号之后,我们可以发现编码相近的地方,大多情况下,他们的实际距离也是相近,少部分编码相差大一些的也是距离很近。但总体来说,Hilbert空间填充比其他的填充曲线如Z-Ordering、Gray更能保持原始数据的性能。
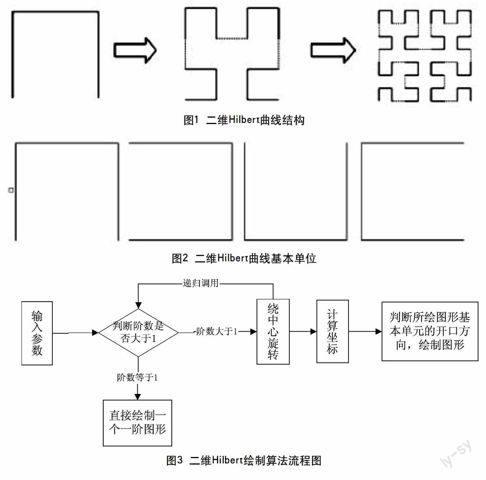
1 二维Hilbert曲线结构
图1是用代码自动生成的一阶,二阶,三阶曲线,从中我们可以发现,当我们把中间的二階曲线填充的正方形分成四块的时候,分割下来最原始的就是图2中的四个图形,我们可以发现四块中各部分的形状跟一阶曲线相同,只是开口方向不一样,再将三阶划分,发现又跟二阶一样,只是方向不同,由此可见,Hilbert曲线是由一个最基本的结构组成,绘制完的Hilbert曲线就是一阶的重复绘制,然后连接起来。而且角度也全是相差90°,可以通过图像旋转来绘制出每个部分。
2 图像旋转
图像旋转即是将一个图像以某个点为旋转中心,逆时针(或顺时针)旋转一定角度,得到的一个图形。这个图形仍然保持与原始图像的形状相同。假设图像左上角坐标为(left,top),右下角坐标为(right,bottom),则图像上任意一点(x,y)绕其中心(xcenter,ycneter)逆时针旋转θ角度后,新的坐标位置(x1,y1)的计算公式为:
xcenter=(width+1)/2+left;
ycenter=(hight+1)/2+top;
x1=(x-xcenter)cosθ-(y-ycenter)sinθ+xcenter;
y1=(x-xcenter)sinθ+(y-ycenter)cosθ+ycenter;
其中width为图像的宽度,hight为图像的高度。通过上面的数学公式就可以通过程序编码,然后得出我们需要的坐标等信息。
该文所述算法里面关键的地方就是需要利用旋转来绘制其他相同的部分,今儿生成整条Hilbert曲线。
3 二维hilbert绘制算法
首先就是要注意各部分的方向,也就是他们与第一个图形的角度,按逆时针算起,然后才可以确定正弦和余弦值。然后在递归调用就可以出现我们需要的那些朝向上下左右的基本图形单元,然后用直线将相邻部分连接起来就可以达到我们的目标。算法流程图如图3所示。
4 结语
Hilbert曲线的各部分构造相同,只是他们各部分的开口方向一样,因此,不管是多少维的Hilbert曲线都比较好实现,只是实现他们的算法简单或复杂、快或慢、高效或低效的区别。二维相对来说简单一些,考虑的相对少一些,不过这可以为生成后面的高维曲线作铺垫。下面的研究方向是对三维Hilbert曲线的绘制算法进行研究。
参考文献
[1] 谢耀华,汤晓安,孙茂印,等.基于分类重排LZW的图像无损压缩算法[J].中国图象图形学报,2010(2):236-241.
[2] 林雪辉,蔡利栋.基于Hilbert曲线的数字图像置乱方法研究[J].中国体视学与图像分析,2004(4):224-227.
[3] LinShen-Yi,Chen,Chih-Shen,LiuLi,et al.Tensor Product Formulation for Hilbert Space-Filling Curves[J].J.Inf.Sci.Eng.2008(24):261-275.
[4] 孙家广.计算机图形学[M].北京:清华大学出版社,1990.

