基于非结构化网格的任意复杂2D RMT有限元模拟
原源, 汤井田, 任政勇*, 周聪, 肖晓, 张林成
1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 4100832 中南大学地球科学与信息物理学院应用地球物理系, 长沙 410083
基于非结构化网格的任意复杂2D RMT有限元模拟
原源1,2, 汤井田1,2, 任政勇1,2*, 周聪1,2, 肖晓1,2, 张林成1,2
1 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 4100832 中南大学地球科学与信息物理学院应用地球物理系, 长沙 410083
射频大地电磁法(RMT)是以潜艇天线发射的射线源等作为场源的一种地球物理勘探方法,目前被广泛应用于近地表工程和环境地球物理勘探.RMT数据解释常采用基于静态假设的大地电磁法(MT)程序,往往会反演出不真实的浅层目标体.为解决这一长期困扰RMT资料解释的问题,本文实现了考虑位移电流的RMT有限元数值模拟.为了处理任意复杂模型,如起伏地形,非结构的三角形网格被用于离散RMT模型.首先通过算例对比,验证了程序的正确性和可靠性.通过Dike模型讨论了空气层厚度对RMT数值解的影响,结果表明当空气层厚度大于1/4波长即可满足精度要求.以山脊模型为例计算了位移电流对RMT响应的影响,表明位移电流的影响会随着山脊高程的增加而增大. 最后通过舒家店实际模型进一步验证了位移电流在RMT中的重要性.
大地电磁; RMT; 有限元; 非结构网格; 位移电流
1 引言
射频大地电磁法(Radio-magnetotelluric)是近几年才逐步发展的一种浅地表地球物理勘探方法.RMT法的测量频段为10~250 kHz,勘探深度为数米到数十米,目前多应用于工程勘探及环境监测(Pedersen et al.,2005,2006; Tezkan et al.,2000,2005; Tezkan and Saraev,2008; Ismail et al.,2011a,2011b; Bastani et al.,2013).
由于RMT法与MT法都是在相应源的远区观测水平电磁场,因而目前在进行RMT资料处理与解释时多是直接套用MT的正反演程序(Newman et al.,2003; Linde and Pedersen,2004; Candansayar and Tezkan,2006,2008),这会导致反演得到的地下电阻率值出现不切实际的极小极大值(Persson and Pedersen, 2002; Kalscheuer et al.,2008),从而得到不合理的解释结果.由于MT法测量频率在数百赫兹内,在该频段,电磁场以感应扩散为主,因此在数值模拟时通常进行准静态假设,忽略位移电流.RMT法的测量频段为10~250 kHz,在该频段内,位移电流不是远远小于传导电流,因而不可忽略位移电流,当地下岩体为结晶类高阻岩石(如石英岩等)时尤其如此(Chave and Jones,2012).因此,实现考虑位移电流的RMT正演程序具有重要意义.
Persson和Pedersen (2002)讨论了一维RMT响应中,位移电流对视电阻率和相位的影响,表明考虑位移电流得到的视电阻率和相位值均低于准静态计算结果,同时文中对层状模型进行反演,得出结论:不考虑位移电流的反演电阻率与实际偏差较大.继均匀半空间和层状模型后,Kalscheuer等(2008)首次研究了二维介质中位移电流对RMT响应的影响,说明了在RMT频段内,当地下电阻率大于10000 Ωm后,位移电流会对计算精度产生较大影响,视电阻率和相位值均低于准静态结果,同时准静态条件下的反演结果会带来虚假构造,导致错误的解释.然而,Kalscheuer等(2008)的工作均是基于平地形的有限差分正演程序,在野外实际工作中,通常面临的是复杂起伏地形,因而开发带地形的RMT程序更具实际意义.
为了解决复杂起伏地形情况下RMT的数据解释问题,本文开发了基于非结构三角形网格的2D带地形RMT有限元正演程序.首先通过一算例对比验证了程序的正确性.由于RMT模拟中存在位移电流,那么TM模式的计算也必须考虑空气层的影响,为此,文中讨论了高精度RMT模拟中空气层厚度的最佳选择.接着,文中讨论了起伏地形下位移电流对数值解的影响.最后通过一实际算例进一步说明在RMT数值模拟中必须考虑位移电流的影响.
2 含空气层的二维RMT问题
2.1 边值问题

图1 求解域Ω=Ω1∪Ω2,上边界Γ1,外边界ΓD为无穷远边界,Γint为内边界,x为二维构造走向方向
假设x方向为构造走向方向(图1),z方向垂直向下,电磁场分量只沿y、z方向有变化,因此二维构造下,电磁场方程可写为(取时间因子eiω t):

(1)

(2)

(3)
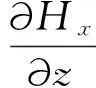
(4)

(5)

(6)
其中ω为角频率,σ为电导率,ε为介电常数,μ0为磁导率.(1)—(3)式定义了TE模式,(4)—(6)式定义了TM模式.
将(6)式两边求∂/∂y,(7)式两边求∂/∂z,并代入(5)式即得TE模式下电场Ex分量满足的Helmholtz方程:


(8)
(7)式(8)式可统一表示为如下所示的偏微分方程:

(9)


在低频情况下,由(4)、(5)式可知,磁场在空气中几乎不变化,因此对于低频问题,如MT问题,TM模式一般不考虑空气.对于RMT来说,由于位移电流在空气中占主导,因此由(4)、(5)式可知,磁场在空气中存在变化,因此RMT问题的TE和TM模式,均要考虑空气层.
本文中计算区域如图1所示,外边界(ΓD)上电位通过层状介质解析解给出,上边界(Γ1)取u=1,内边界(Γint)根据场切向分量连续给出.综上,边值问题中的边界条件如下:
u=r(x,z),onΓD
(10)
(11)
2.2 有限元近似
网格剖分可分为两种类型,结构化网格与非结构化网格.结构化的网格在区域加密时会导致不必要的外部节点增加,从而增加额外的计算量,且结构化网格在对复杂地形及地下构造模拟中不够灵活(Li and Spitzer,2002; Mitsuhata and Uchida,2004;谭捍东等,2003;胡祖志等,2006;胡祥云等,2012;董浩等,2014).因而,非结构网格以其灵活性近些年广泛应用于地球物理数值模拟领域(Franke et al.,2007; Ren and Tang, 2010;Ren et al.,2013;刘长生等,2010;吴小平等,2015).
本文中,求解域Ω进行网格离散时采用非结构的三角形网格(Shewchuk,1996),以保证灵活模拟复杂地质构造及地形.在离散过程中,通过设定每个三角形单元的最小角不低于30°来保证单元质量,同时通过给定局部区域单元片面积最大值来实现网格的局部加密.进行网格剖分时,首先根据最低频率确定最大趋肤深度δmax,剖分区域边界距离不低于10δmax;在电阻率突变界面附近控制单元大小进行局部加密;与MT法不同,RMT法计算TM模式的磁场时,空气中的磁场不能看做常数,因此TM模式也需要考虑空气层,而空气中的网格剖分也要仔细考虑.在高频情况下,电磁场在空气中以电磁波的形式向外传播,空气中电磁波的传播速度为光速c=3×108m·s-1,根据c=λ·f,其中λ为波长,f为频率,据此可计算出不同频率下的波长,本文中网格剖分时最短波长内保证有20~30个节点.
基于线性三角形有限单元,通过求离散边值问题,从而获得关于方程(9)中未知数u的线性方程组:
AU=0,
(12)
式中,U为方程(9)中u的一维向量,刚度矩阵A为稀疏对称复数矩阵.本文通过三个一维数组仅存储矩阵的非零元素,从而节省计算内存.采用Intel Math Kernel Library(Intel,2010)中的直接求解器PARDISO(Schenk and Gärtner,2004)来求解线性方程组.求出TE及TM模式的电场Ex和磁场Hx后,本文采用四点差分求得相应的磁场Hy和电场Ey.最后,阻抗、视电阻率ρij和相位φij通过如下计算公式获得:

(13)

(14)
φij=arctan(Im(Zij)/Re(Zij)),ij=xy,yx,
(15)
其中,Re、Im分别表示复数的实部与虚部.
3 数值算例
本节首先计算了Kalscheuer等(2008)文中的模型,并进行了结果对比,验证了程序正确性;然后以Dike模型为例研究了空气层厚度对数值解的影响;接着讨论了起伏地形下,位移电流的影响规律;最后通过舒家店的实际地质模型说明了位移电流对实际数据的影响.文中所有计算均在CPU为2.3GHz,RAM为2GB的个人计算机上完成.
3.1 均匀半空间中一矩形异常体


图2 均匀半空间中赋存一矩形异常体,半空间电阻率为10000 Ωm,相对介电常数为5,矩形电阻率为1000 Ωm
图4、图5分别为TE、TM模式下计算得到的视电阻率及相位曲线,其中线条为本文有限元计算结果,符号为Kalscheuer等(2008)的有限差分程序计算结果,二者均考虑位移电流.从图中可看出本文计算结果与Kalscheuer等(2008)的结果吻合,表明程序正确.
3.2 空气层厚度对RMT数值解的影响
在RMT有限元模拟中,由于位移电流项的存在,即使TM模式也不可忽略空气层,为此,本节讨论空气层厚度对数值解的影响.图6为Dike模型示意图,背景电阻率ρ2=10000 Ωm,相对介电常数为5,中间断层电阻率ρ1=1000 Ωm.

图3 局部网格剖分示意图

图4 图2所示模型考虑位移电流的TE模式(a)视电阻率及(b)相位曲线,频率分别为10 kHz、100 kHz、250 kHz

图5 图2所示模型考虑位移电流的TM模式(a)视电阻率及(b)相位曲线,图例与图4相同

图6 Dike模型示意图
表1为不同空气层厚度下网格剖分后的单元节点信息、计算误差及计算耗时.计算频率为250 kHz,空气层厚度从0.01λ~10λ,其中λ为波长,根据c=λ·f计算而来,c为光速,因此λ=1200 m.从表1中可看出,当空气层厚度大于0.2λ, TE/TM模式视电阻率及相位的最大误差均在1%以内;当空气层厚度小于0.2λ时,TE/TM模式视电阻率及相位的最大相对误差均随空气层厚度的减小而增大.因此,在数值计算中,保证空气层厚度大于0.2λ即可满足精度要求.

表1 对不同空气层厚度剖分后的网格信息、计算误差及计算量
图7、图8分别为不同空气层厚度下计算的所有测点的TE/TM模式视电阻率、相位及其相应误差.图中展示的是几个典型空气层厚度的结果.所有的误差计算均与10λ的结果进行对比,无论TE还是TM模式,当空气层厚度大于0.2λ时,TE/TM模式的视电阻率及相位所有测点的误差均在1%以内,而当空气层厚度为0.1λ时,TE模式视电阻率最大误差为1.66%,相位最大误差为2.08%;TM模式视电阻率最大误差为1.65%,相位最大误差为1.50%.对比TE模式所有测点的误差曲线可发现,除了局部个别测点外,几乎所有测点的误差均随着空气层厚度的减小而增大,而TM模式的误差曲线对这一规律的反映则不够明显,这是因为TM模式受横向异常体影响较大所致.
3.3 起伏地形模型
本节采用图9所示的模型(Wannamaker et al.,1986)讨论不同高程下位移电流的影响.图9中共给出了3个测试模型,余弦型山脊的高程分别为100 m、300 m、600 m,电阻率均为10000 Ωm,相对介电常数为5,计算的三个频率为10 kHz、100 kHz、250 kHz.
为保证结果可靠,本节三个模型均采用较密的网格剖分,以降低计算误差.网格剖分参数和计算耗时如表2所示.

表2 起伏地形模型网格剖分参数表

图7 不同空气层厚度下得到的TE模式(a)视电阻率、(c)相位及其相应误差(b)(d).计算频率f=250 kHz,空气层厚度分别取10λ、1λ、0.25λ、0.1λ;计算误差均与10λ的结果进行对比

图8 同图7,但为Dike模型的TM模式结果对比

图9 三个模型均为余弦型山脊,山脊高程分别为100 m、300 m、600 m,三个模型的电阻率均为10000 Ωm,相对介电常数为5
图10为考虑位移电流和准静态情况下计算的视电阻率及相位曲线,计算频率为10 kHz、100 kHz、250 kHz.从不同频点的结果对比来看,10 kHz下考虑位移电流和不考虑位移电流的曲线都基本重合,说明本算例中位移电流在10 kHz的频段处影响不大,而计算频率为100 kHz、250 kHz时,考虑位移电流的视电阻率曲线和相位曲线均出现下掉现象,其中相位曲线更为严重,表明对于本算例中的模型参数而言,当频率大于100 kHz后,位移电流对视电阻率的影响不可忽略,而对相位曲线的影响从频率为20 kHz后就必须考虑.
图11是频率为250 kHz下考虑位移电流和准静态条件下计算得到的视电阻率及相位绝对误差,将三个模型计算结果对比,发现当山脊高程越大,坡度越陡,位移电流的影响就越大.从图11a,11c可看出,TE模式的视电阻率及相位的最大误差发生在山脊两侧,而山脊顶部则出现局部极大值;而图11b,11d显示TM模式视电阻率及相位的最大误差也发生在山脊两侧,但山脊顶部无较明显的极值.
3.4 实际模型
实际模型来自安徽铜陵矿集区舒家店地区某剖面(图12),该剖面长3.8 km,具备以下两个特点:该区域存在高阻闪长岩,位移电流可能会造成显著影响;地形起伏明显,有两个山脊,地形对位移电流的影响不可忽略.

图14为TE/TM模式下考虑位移电流和准静态条件下的视电阻率及相位误差.从图中可看出,误差整体随着频率的增加而增大;在x=-1000 m和x=500 m的高阻石英闪长岩体区域,考虑位移电流的结果和准静态结果存在明显的误差,而在x=-1000 m的山脊处这种误差更大.值得一提的是,相位受位移电流影响比视电阻率更为显著,即使x=1300 m处,粉砂岩电阻率为420 Ωm的情况下,在高频和山脊的共同作用下,相位也出现了明显的误差.ρTE的最大相对误差为14.5%,位于x=-950 m处,而在该处附近的误差也都在10%左右,此外,在x=-1600 m、x=500 m以及x=1500 m附近的误差也都在5%以上;ρTM的最大相对误差高达78%,这是因为TM模式横向分辨率高,在电阻率分界面处二者计算结果有较大误差,ρTM也主要分布在两个山脊处和x=400 m的分界面处.

图10 (a)(c)为model-1的TE/TM模式的视电阻率曲线,(b)(d)为model-1的TE/TM模式的相位曲线,计算频率为10 kHz、100 kHz、250 kHz

图11 考虑位移电流和不考虑位移电流的视电阻率及相位误差对比,频率为250 kHz

图12 舒家店地质综合剖面图(安徽省地质调查院提供)

图13 舒家店地球物理模型及网格剖分示意图

图14 TE/TM模式下考虑位移电流和准静态条件下的视电阻率及相位误差曲线

图15 考虑位移电流条件下计算的位移电流密度和传导电流密度,计算频率f=250 kHz
图15为考虑位移电流时计算的位移电流密度和传导电流密度,计算频率为250 kHz.图15a,15b为电流密度的模.图15c为位移电流密度占总电流密度的百分比.从图15c中可看出,空气中位移电流密度占100%,也就是说空气中仅存在位移电流,无传导电流.在地下砂岩、粉砂岩对应的低阻区,位移电流密度在总电流密度中所占的比例为1%.花岗闪长岩区域的位移电流密度占3%左右.对于电阻率很高的石英闪长岩,位移电流密度所占比例达到10%,因此,在RMT数值模拟中不可忽略位移电流.
4 讨论与结论
大多数RMT的资料解释多是直接应用MT程序,忽略了位移电流的影响,这可能导致错误的解释结果;并且,在起伏地形条件下,位移电流的影响更为显著.针对这一问题,本文编写了起伏地形下的全电流2D RMT有限元程序.通过非结构的三角形单元实现了任意复杂模型的离散化,同时,程序采用局部加密策略获得了高精度的数值解.
由于位移电流的存在,空气层中磁场的偏导数不能近似为0,因而在对TM模式进行有限元离散时也必须考虑空气层.通过Dike模型讨论了空气层厚度对数值解的影响,当空气层厚度大于1/4波长即可保证TE/TM模式的有限元解的误差均在1%以内.
根据电流公式,位移电流随频率的升高而增大,传导电流随介质电阻率的增大而减小,因此在高频高阻情况下,位移电流在总电流中所占的比重就越大.文中结果表明,考虑位移电流情况下得到的视电阻率和相位曲线相比于准静态条件下的计算结果会出现下掉现象,且频率越高下掉越明显,这是因为位移电流项的引入增大了总电流密度,而总电流密度的增大会使得地下介质的电导率特性放大,从而导致视电阻率曲线下掉.数值算例表明,当背景电阻率为10000 Ωm时,频率大于100 kHz后,位移电流对视电阻率的影响不可忽略,而对相位曲线的影响从频率为20 kHz后就必须考虑.在背景电阻率与频率不变的情况下,地形起伏也会影响位移电流,地形高程越大,考虑位移电流计算的视电阻率与准静态条件下得到的视电阻率差异也越大,同时,数值结果表明差异最大的地方位于山脊的两侧.
通过铜陵舒家店矿床的实际地质模型,分别计算了传导电流和位移电流,结果表明在高阻花岗闪长岩地区位移电流不可忽略,会对模拟、观测结果造成显著的影响.如忽略位移电流,采用现有的MT程序进行RMT反演解释,势必带来结果的偏差,进而影响资料解释的准确度.而采用本文提供的全电流起伏地形模拟程序,可以获得更为准确的模拟结果.
基于本文的研究成果,作者将进一步开发针对RMT的反演程序.
致谢 感谢Shewchuk提供的非结构三角形网格剖分开源代码Triangle,感谢Schenk提供的方程组求解器PARDISO,感谢网格剖分可视化软件PARAVIEW的作者,感谢安徽省地质调查院提供舒家店矿床地质模型.同时感谢舒家店野外物性测量人员王显莹、张弛等.
Bastani M, Persson L, Beiki M, et al. 2013. A radio magnetotelluric study to evaluate the extents of a limestone quarry in Estonia.GeophysicalProspecting, 61(3): 678-687.
Candansayar M E, Tezkan B. 2006. A comparison of different radiomagnetotelluric data inversion methods for buried waste sites.JournalofAppliedGeophysics, 58(3): 218-231. Candansayar M E, Tezkan B. 2008. Two-dimensional joint inversion of radiomagnetotelluric and direct current resistivity data.GeophysicalProspecting, 56(5): 737-749.
Chave A D, Jones A G. 2012. The Magnetotelluric Method: Theory and Practice. Cambridge: Cambridge University Press. Dong H, Wei W B, Ye G F, et al. 2014. Study of Three-dimensional magnetotelluric inversion including surface topography based on finite-difference method.ChineseJ.Geophys. (in Chinese), 57(3): 939-952, doi: 10.6038/cjg20140323.
Franke A, Börner R U, Spitzer K. 2007. Adaptive unstructured grid finite element simulation of two-dimensional magnetotelluric fields for arbitrary surface and seafloor topography.GeophysicalJournalInternational, 171(1): 71-86.
Hu X Y, Li Y, Yang W C, et al. 2012. Three-dimensional magnetotelluric parallel inversion algorithm using data space method.ChineseJ.Geophys. (in Chinese), 55(12): 3969-3978, doi: 10.6038/j.issn.0001-5733.2012.12.009.
Hu Z Z, Hu X Y, He Z X. 2006. Pseudo-Three-Dimensional magnetotelluric inversion using nonlinear conjugate gradients.ChineseJ.Geophys. (in Chinese), 49(4): 1226-1234, doi: 10.3321/j.issn:0001-5733.2006.04.039.
Intel. 2010. Intel Math Kernel Library. Linear Solver Basics.Ismail N, Schwarz G, Pedersen L B. 2011a. Investigation of groundwater resources using controlled-source radio magnetotellurics (CSRMT) in glacial deposits in Heby, Sweden.JournalofAppliedGeophysics, 73(1): 74-83.
Ismail N, Pedersen L. 2011b. The electrical conductivity distribution of the Hallandsås Horst, Sweden: a controlled source radiomagnetotelluric study.NearSurfaceGeophysics, 9(1): 45-54.
Kalscheuer T, Pedersen L B, Siripunvaraporn W. 2008. Radiomagnetotelluric two-dimensional forward and inverse modelling accounting for displacement currents.GeophysicalJournalInternational, 175(2): 486-514.
Li Y G, Spitzer K. 2002. Three-dimensional DC resistivity forward modelling using finite elements in comparison with finite-difference solutions.GeophysicalJournalInternational, 151(3): 924-934.
Linde N, Pedersen L B. 2004. Characterization of a fractured granite using radio magnetotelluric (RMT) data.Geophysics, 69(5): 1155-1165.
Liu C S, Tang J T, Ren Z Y, et al. 2010. Three-dimension magnetotellurics modeling by adaptive edge finite-element using unstructured meshes.JournalofCentralSouthUniversity(ScienceandTechnology) (in Chinese), 41(5): 1855-1859.
Mitsuhata Y, Uchida T. 2004. 3D magnetotelluric modeling using the T-finite-element method.Geophysics, 69(1): 108-119.
Newman G A, Recher S, Tezkan B, et al. 2003. 3D inversion of a scalar radio magnetotelluric field data set.Geophysics, 68(3): 791-802. Pedersen L B, Bastani M, Dynesius L. 2005. Groundwater exploration using combined controlled-source and radiomagnetotelluric techniques.Geophysics, 70(1): G8-G15. Pedersen L B, Bastani M, Dynesius L. 2006. Some characteristics of the electromagnetic field from radio transmitters in Europe.Geophysics, 71(6): G279-G284.
Persson L, Pedersen L B. 2002. The importance of displacement currents in RMT measurements in high resistivity environments.JournalofAppliedGeophysics, 51(1): 11-20.
Ren Z Y, Tang J T. 2010. 3D direct current resistivity modeling
with unstructured mesh by adaptive finite-element method.Geophysics, 75(1): H7-H17.
Ren Z Y, Kalscheuer T, Greenhalgh S, et al. 2013. A goal-oriented adaptive finite-element approach for plane wave 3-D electromagnetic modelling.GeophysicalJournalInternational, 194(2): 700-718.
Schenk O, Gärtner K. 2004. Solving unsymmetric sparse systems of linear equations with PARDISO.FutureGenerationComputerSystems, 20(3): 475-487.
Shewchuk J R. 1996. Triangle: Engineering a 2D quality mesh generator and Delaunay triangulator. ∥Lin M C, Manocha D eds. Applied Computational Geometry Towards Geometric Engineering. Berlin Heidelberg: Springer, 1148: 203-222.
Tan H D, Yu Q F, Booker J, et al. 2003. Magnetotelluric three-dimensional modeling using the staggered-grid finite difference method.ChineseJ.Geophys. (in Chinese), 46(5): 705-711, doi: 10.3321/j.issn:0001-5733.2003.05.019. Tezkan B, Hördt A, Gobashy M. 2000. Two-dimensional radiomagnetotelluric investigation of industrial and domestic waste sites in Germany.JournalofAppliedGeophysics, 44(2-3): 237-256.
Tezkan B, Georgescu P, Fauzi U. 2005. A radiomagnetotelluric survey on an oil-contaminated area near the Brazi Refinery, Romania.GeophysicalProspecting, 53(3): 311-323.
Tezkan B, Saraev A. 2008. A new broadband radiomagnetotelluric instrument: applications to near surface investigations.NearSurfaceGeophysics, 6(4): 245-252. Wannamaker P E, Stodt J A, Rijo L. 1986. Two-dimensional topographic responses in magnetotellurics modeled using finite elements.Geophysics, 51(11): 2131-2144.
Wu X P, Liu Y, Wang W. 2015. 3D resistivity inversion incorporating topography based on unstructured meshes.ChineseJ.Geophys. (in Chinese), 58(8): 2706-2717, doi: 10.6038/cjg20150808.
附中文参考文献
董浩, 魏文博, 叶高峰等. 2014. 基于有限差分正演的带地形三维大地电磁反演方法. 地球物理学报, 57(3): 939-952, doi: 10.6038/cjg20140323.
胡祥云, 李焱, 杨文采等. 2012. 大地电磁三维数据空间反演并行算法研究. 地球物理学报, 55(12): 3969-3978, doi: 10.6038/j.issn.0001-5733.2012.12.009.
胡祖志, 胡祥云, 何展翔. 2006. 大地电磁非线性共轭梯度拟三维反演. 地球物理学报, 49(4): 1226-1234, doi: 10.3321/j.issn:0001-5733.2006.04.039.
刘长生, 汤井田, 任政勇等. 2010. 基于非结构化网格的三维大地电磁自适应矢量有限元模拟. 中南大学学报(自然科学版), 41(5): 1855-1859.
谭捍东, 余钦范, Booker J等. 2003. 大地电磁法三维交错采样有限差分数值模拟. 地球物理学报, 46(5): 705-711, doi: 10.3321/j.issn:0001-5733.2003.05.019. 吴小平, 刘洋, 王威. 2015. 基于非结构网格的电阻率三维带地形反演. 地球物理学报, 58(8): 2706-2717, doi: 10.6038/cjg20150808.
(本文编辑 何燕)
Two-dimensional complicated radio-magnetotelluric finite-element modeling using unstructured grids
YUAN Yuan1,2, TANG Jing-Tian1,2, REN Zheng-Yong1,2*, ZHOU Cong1,2, XIAO Xiao1,2, ZHANG Lin-Cheng1,2
1KeyLaboratoryofMetallogenicPredictionofNonferrousMetalsandGeologicalEnvironmentMonitoring,MinistryofEducation,CentralSouthUniversity,Changsha410083,China2InstituteofAppliedGeophysics,SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China
As a newly developed geophysical exploration method, the radio-magnetotelluric (RMT) method is widely used in near-surface engineering and environment geophysical investigation. Since the interpretation of RMT data usually adopts the magnetotelluric (MT) forward modeling routine, in which displacement currents are generally neglected, the inverted conductivity model may not correctly reflect the true conductivity structure in the shallow subsurface. To solve this issue, we developed a finite-element forward modeling code for RMT data, in which displacement currents are considered. With this code, we analyze the dielectric effect of displacement currents on RMT responses over resistive subsurface models.First, we derived the boundary value problem (BVP) about the EM field components by the Galerkin method, in which the displacement currents were considered. Then we used the finite element method and PARDISO solver to calculate the electric and magnetic field components. To deal with complicated structure and surface topography, unstructured triangle grids were adopted for mesh generation. To improve the computation accuracy, the local refinement was used. At last, we developed a forward modeling code for RMT data with the consideration of displacement currents and analyzed the effect of displacement currents on 2D TM-mode, TE-mode data, which measured with the RMT method at frequencies between 10 and 300 kHz.First, a synthetic model was used to verify the correction of our new code. The result shows that the response calculated by our code agrees well with other results. Utilizing the Dike model, the effect of the thickness of the air layer on accuracy of numerical solutions was investigated. The result shows that when the thickness of the air layer is greater than 1/4 wavelength, highly accurate solutions can be guaranteed. Then the impact of displacement currents on RMT data with ridge terrain was studied on a hill model with complicated topography. From this model, the following results can be demonstrated: (1) The effect of displacement currents would increase with increasing height of the hill and the corner of hill was more easier to be affected. (2) The phase curves are more likely to be affected than apparent resistivity curves at high frequency. (3) The effect of displacement currents on apparent resistivity cannot be neglected when the frequency is larger than 100 kHz and the effect on phase must be considered when the frequency is larger than 20 kHz. Finally, a field model was studied to further demonstrate the importance of displacement currents in the RMT method. The results show that: (1) The error caused by displacement currents increases with frequency. (2) The apparent resistivity of TM-mode is more easily to be affected by displacement currents than TE-mode apparent resistivity. (3) For the area of quartz diorite with high resistivity, the percentage of displacement current density in all current density can be 10%. It is clear that displacement currents must be considered in RMT forward modeling.With numerical calculations, we demonstrated the effect of displacement currents on 2D RMT data. Forward modeling confirms that responses computed in the quasi-static approximation become increasingly inaccurate with rising frequency and strongly affected by terrain. However, RMT data processing and interpretation are mostly based on the MT program in recent years, which may result in incorrect structure. Based on the work in this paper, the author will develop RMT inversion code with consideration of displacement current.
Magnetotelluric; RMT; Finite element method; Unstructured grids; Displacement currents
国家深部探测专项第3项目(SinoProbe-03),“十二五”国家科技支撑计划课题(2011BAB04B01),国家自然科学基金(41574120),国家高技术研究发展计划(863计划)(2014AA06A602),国家重点基础研究发展计划(973计划)(2015CB060201),中南大学创新驱动计划(2015CX008)资助.
原源,女,1989年生,博士研究生,从事电磁法有限元正反演研究. E-mail: 13657400521@163.com
*通信作者 任政勇,男,1983年生,副教授,主要从事电磁场数值模拟及反演研究. E-mail: renzhengyong@csu.edu.cn
10.6038/cjg20151229.
10.6038/cjg20151229
P631
2014-10-27,2015-06-18收修定稿
原源, 汤井田, 任政勇等. 2015. 基于非结构化网格的任意复杂2D RMT有限元模拟.地球物理学报,58(12):4685-4695,
Yuan Y, Tang J T, Ren Z Y, et al. 2015. Two-dimensional complicated radio-magnetotelluric finite-element modeling using unstructured grids.ChineseJ.Geophys. (in Chinese),58(12):4685-4695,doi:10.6038/cjg20151229.

