Comparison with Molecular Surface Electrostatic Potential and Thermal Reactivity of Nitramines

Svatopluk Zeman, Zdeněk Friedl, Monika Bartošková, Qi-Long YAN

(1. Institute of Energetic Materials, Faculty of Chemical Technology, University of Pardubice, CZ-532 10 Pardubice, the Czech Republic; 2. Faculty of Chemistry, Brno University of Technology, CZ-612 00 Brno, the Czech Republic)

1 Introduction

In the past 20 years, the preferred tools for dealing with sensitivities of high energy materials (HEMs) have involved quantum chemistry, predominantly DFT calculation methods[1-4]. A modification of this approach is the use of molecular surface electrostatic potentialVS(r) (ESP) which is created by the nuclei and electrons of a molecule in the surrounding space. ESP is given by Eq. (1)[5].

(1)

whereZAis the charge on nucleusA, which is located at distanceRA, andρ(r) describes the electron density of the molecule.

The high levels of imbalance between the maximum positive,VS,max, and minimum negative,VS,min, values of molecular surface electrostatic potentials (ESPs) in sensitive energetic materials should correspond to the high energetic content of these compounds (increasing the explosive strength is usually accompanied by an increase in sensitivity[6]). In an earlier paper[10]we suggested a new valueVS,Σ, described by the sum.

VS,Σ=VS,max+VS,min

(2)

The relationships of these summed potentialsVS,Σto the real state were found for the first time in studying the detonation of nitramines[7]and they are also a topic of this paper.

One of the most studied stimuli for initiating HEMs is initiation by heat. However, the basic problem of defining the kinetics and mechanism of the thermal decomposition of these materials lies in the strong dependence of the corresponding kinetic parameters on temperature, pressure, and the materials used that are in contact with the sample decomposed[8]. Hence, obtaining similar results from thermal analyses of energetic materials using different methods and/or different types of apparatus of different origin is very rare[8-10]. So far the most reliable results in this area are the theoretical and practical findings obtained by Russian scientists on the basis of their manometric method (see Refs. [9,11-13] and quotations therein). The data obtained by this method are known to correspond to the non-autocatalyzed stage of thermal decomposition of the given material (i.e. to molecular structure[9, 10-12]), and also to the absolute values of the corresponding Arrhenius parameters. This paper considers the relationship of these data to electrostatic surface potentials defined by the sum described in equation 2. Nitramines have been chosen for this purpose because of their relatively simple molecular structure and their reactivity, amply described in the literature[11-16]. This paper might also be taken as a continuation of the previous study[7].

2 Procedures

2.1 Arrhenius Parameters of Thermal Decomposition

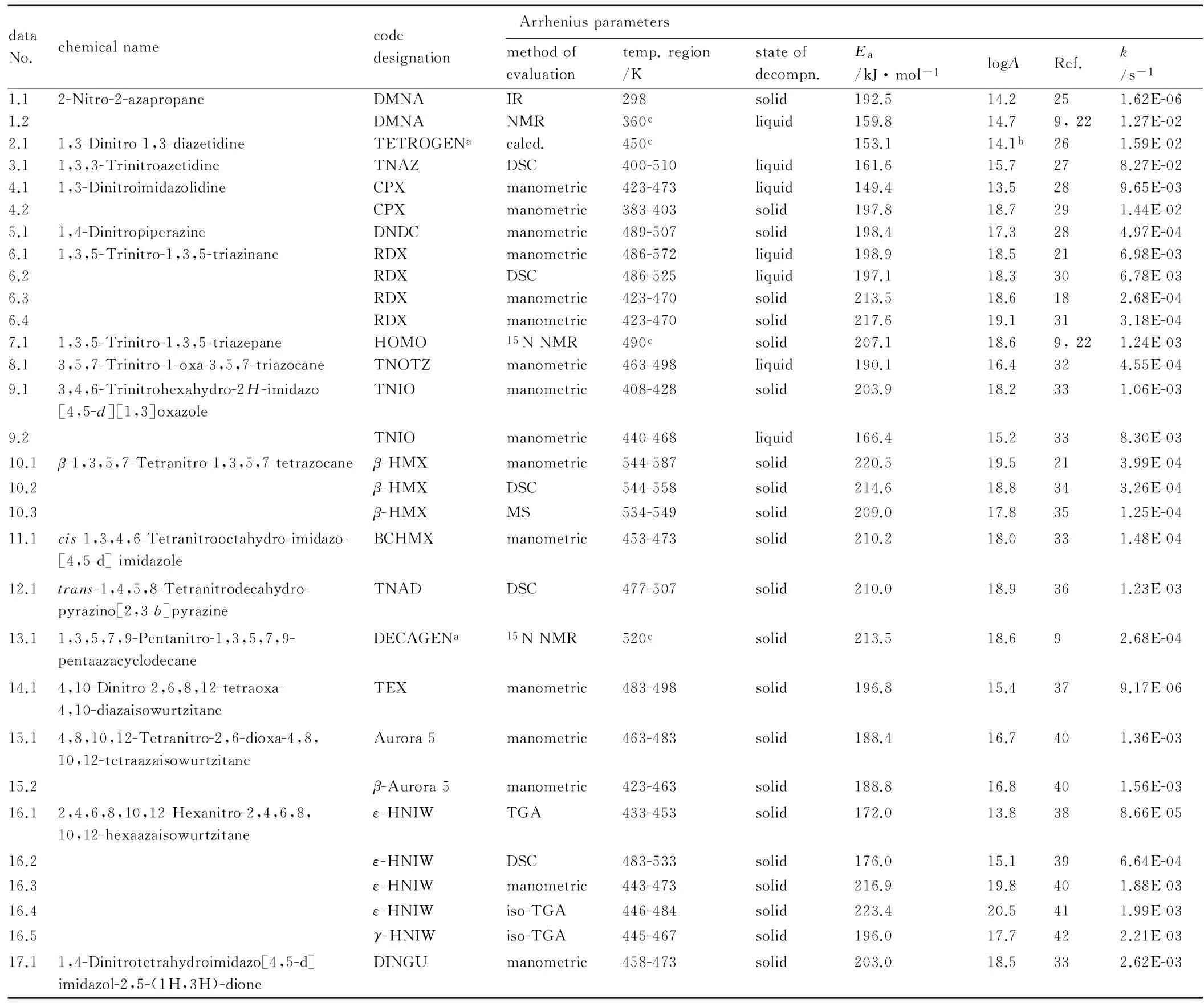
The Russian manometric method (RMM) is a special kind of Vacuum Stability Test[11,13,17-21]which uses a glass compensating manometer of the Bourdon type to examine the kinetics of thermolysis of energetic materials in a vacuum. TheEaand logAvalues, obtained by this method, are the main data used in this paper and, as already mentioned, correspond to the uni-molecular non-autocatalyzed decomposition of the nitramines studied. It is possible to apply here also kinetic data from other manometric methods (e.g. Robertson′s method[21]) or some thermoanalytical methods, particularly the differential scanning calorimetry (DSC)[30, 34, 36]and partial TGA[38, 41-42], which are directly compatible with the RMM results. The above-mentioned data can be also obtained via theoretical prediction using the outputs of the15N NMR spectroscopy[9, 12, 15, 22]. The Arrhenius parameters used are presented in Table 1.

2.2 Nitramines

The structural formulas of the individual nitramines studied are shown in Scheme 1.

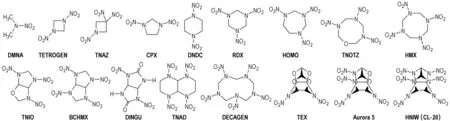
Scheme 1 Structural formulas of the nitramines studied

Table 1 A list of the nitramines studied, showing the Arrhenius parameters of their low-temperature thermal decomposition including the calculated rate constantskfor uni-molecular decomposition at 230 ℃

dataNo.chemicalnamecodedesignationArrheniusparametersmethodofevaluationtemp.region/Kstateofdecompn.Ea/kJ·mol-1logARef.k/s-11.12-Nitro-2-azapropaneDMNAIR298solid192.514.2251.62E-061.2DMNANMR360cliquid159.814.79,221.27E-022.11,3-Dinitro-1,3-diazetidineTETROGENacalcd.450c153.114.1b261.59E-023.11,3,3-TrinitroazetidineTNAZDSC400-510liquid161.615.7278.27E-024.11,3-DinitroimidazolidineCPXmanometric423-473liquid149.413.5289.65E-034.2CPXmanometric383-403solid197.818.7291.44E-025.11,4-DinitropiperazineDNDCmanometric489-507solid198.417.3284.97E-046.11,3,5-Trinitro-1,3,5-triazinaneRDXmanometric486-572liquid198.918.5216.98E-036.2RDXDSC486-525liquid197.118.3306.78E-036.3RDXmanometric423-470solid213.518.6182.68E-046.4RDXmanometric423-470solid217.619.1313.18E-047.11,3,5-Trinitro-1,3,5-triazepaneHOMO15NNMR490csolid207.118.69,221.24E-038.13,5,7-Trinitro-1-oxa-3,5,7-triazocaneTNOTZmanometric463-498liquid190.116.4324.55E-049.13,4,6-Trinitrohexahydro-2H-imidazo[4,5-d][1,3]oxazoleTNIOmanometric408-428solid203.918.2331.06E-039.2TNIOmanometric440-468liquid166.415.2338.30E-0310.1β-1,3,5,7-Tetranitro-1,3,5,7-tetrazocaneβ-HMXmanometric544-587solid220.519.5213.99E-0410.2β-HMXDSC544-558solid214.618.8343.26E-0410.3β-HMXMS534-549solid209.017.8351.25E-0411.1cis-1,3,4,6-Tetranitrooctahydro-imidazo-[4,5-d]imidazoleBCHMXmanometric453-473solid210.218.0331.48E-0412.1trans-1,4,5,8-Tetranitrodecahydro-pyrazino[2,3-b]pyrazineTNADDSC477-507solid210.018.9361.23E-0313.11,3,5,7,9-Pentanitro-1,3,5,7,9-pentaazacyclodecaneDECAGENa15NNMR520csolid213.518.692.68E-0414.14,10-Dinitro-2,6,8,12-tetraoxa-4,10-diazaisowurtzitaneTEXmanometric483-498solid196.815.4379.17E-0615.14,8,10,12-Tetranitro-2,6-dioxa-4,8,10,12-tetraazaisowurtzitaneAurora5manometric463-483solid188.416.7401.36E-0315.2β-Aurora5manometric423-463solid188.816.8401.56E-0316.12,4,6,8,10,12-Hexanitro-2,4,6,8,10,12-hexaazaisowurtzitaneε-HNIWTGA433-453solid172.013.8388.66E-0516.2ε-HNIWDSC483-533solid176.015.1396.64E-0416.3ε-HNIWmanometric443-473solid216.919.8401.88E-0316.4ε-HNIWiso-TGA446-484solid223.420.5411.99E-0316.5γ-HNIWiso-TGA445-467solid196.017.7422.21E-0317.11,4-Dinitrotetrahydroimidazo[4,5-d]imidazol-2,5-(1H,3H)-dioneDINGUmanometric458-473solid203.018.5332.62E-03

Note: a) a substance which has not yet been synthesized, their data were predicted [9, 15, 43]; b) calculated in Ref.[22]; c) the estimated values for thekvalues calculation (estimation on the basis of its predicted physical stability in Ref.[43])

2.3 Calculations

The equilibrium geometries of all the nitramines studied were optimized by means of the Spartan′10 Win-P program[23]at the DFT B3LYP/6-311+G(d,p)//6-311+G(d,p) level, and the electron energies obtained were refined by the unscaled ZPE correction. The molecular surface electrostatic potentials,VS(r), were calculated at the DFT B3LYP/6-31G(d,p)//6-311+G(d,p) level, and the molecular surface was taken to be 0.001 e·au-3contour of the electron density. The results are shown in Table 2. The sums of theVS,maxandVS,minpotentials (i.e.VS,Σ) from Table 2 give both positive and negative values; this is perfectly understandable because the above-mentioned theoretical assumption of the zero energy is not logically real.

2.4 Heat of Fusion

Relationships exist between the bond dissociation energies of the weakest bonds in the HEM molecules and the intensity of intermolecular interactions in their molecular crystal, i.e. the work needed for formation of defects in the crystal lattices[45]. This work might be represented by heat of fusion,Hm,tr, which is here defined as a sum of the heats of all the polymorphous transitions and of the heat of melting[24]. TheHm,trvalues for the majority of the nitramines studied are summarized in Table 2.

Table 2 A summary of computed surface electrostatic potentials and published heats of fusion of the nitramines studied

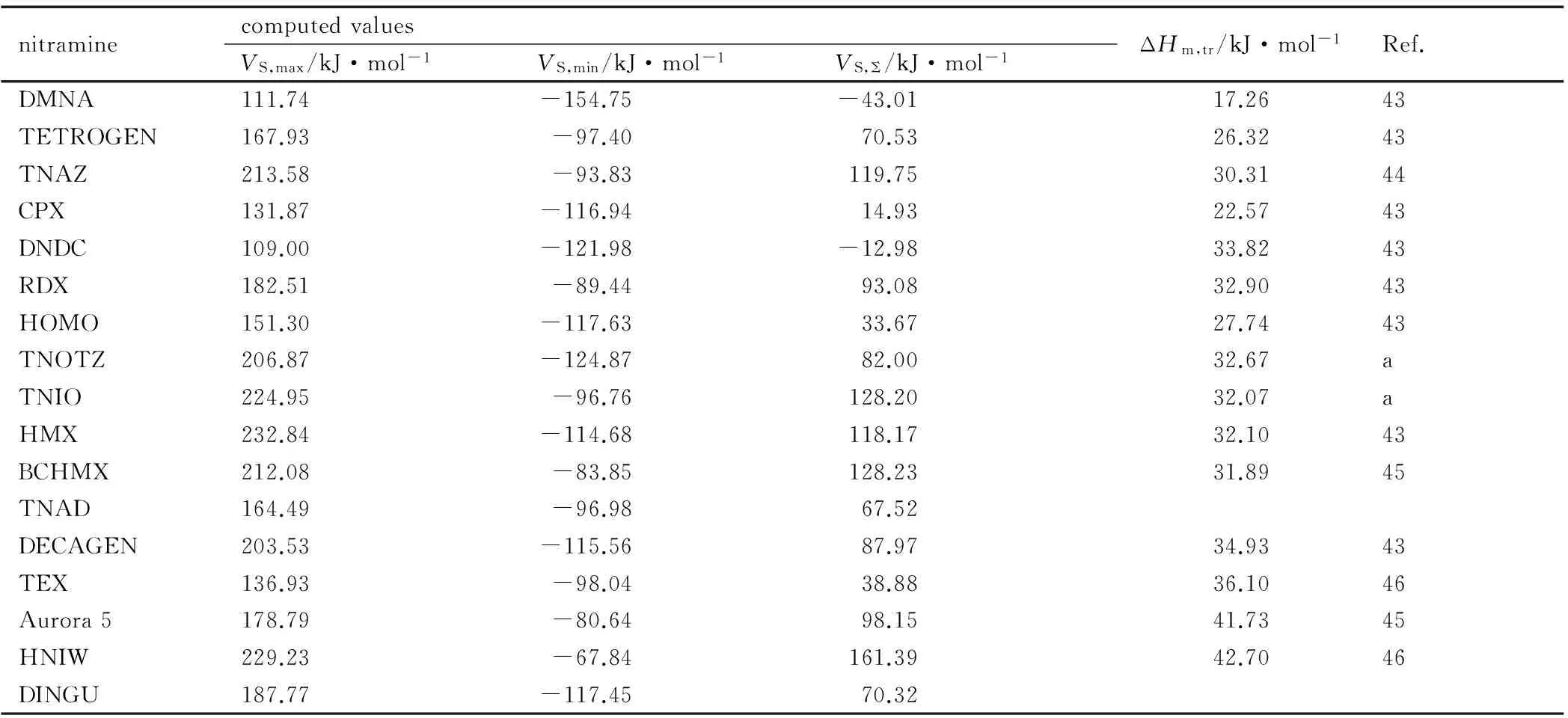
nitraminecomputedvaluesVS,max/kJ·mol-1VS,min/kJ·mol-1VS,Σ/kJ·mol-1ΔHm,tr/kJ·mol-1Ref.DMNA111.74-154.75-43.0117.2643TETROGEN167.93-97.4070.5326.3243TNAZ213.58-93.83119.7530.3144CPX131.87-116.9414.9322.5743DNDC109.00-121.98-12.9833.8243RDX182.51-89.4493.0832.9043HOMO151.30-117.6333.6727.7443TNOTZ206.87-124.8782.0032.67aTNIO224.95-96.76128.2032.07aHMX232.84-114.68118.1732.1043BCHMX212.08-83.85128.2331.8945TNAD164.49-96.9867.52DECAGEN203.53-115.5687.9734.9343TEX136.93-98.0438.8836.1046Aurora5178.79-80.6498.1541.7345HNIW229.23-67.84161.3942.7046DINGU187.77-117.4570.32

Note: a) Predicted in this paper by means of a relation with negative slope in Fig.4.

2.5 Isothermal Thermo-gravimetry

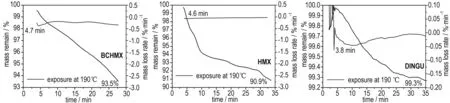
Thermo-gravimetry(TG,Netzsch 209F3 instrument, Al2O3crucible) was used for explaining certain particularities of thermal decomposition of BCHMX, HMX andε-HNIW, and this involved isothermal exposure at 190 ℃ for a period of 100 min, using a sample mass of about 1.35-1.45 mg under 30 mL·min-1dynamic nitrogen atmosphere. The results of this thermal exposure are shown in Fig.1. In another set of measurements, such isothermal exposure was interrupted after 30 minutes and the exposed samples were submitted to investigation using a Scanning Electron Microscope (SEM) together with the original crystals of all three nitramines; the SEM pictures are presented as Fig.2.

3 Results and Discussion

Already in paper[7]it has been shown that those nitramines with the highest values of energy content also have the highestVS,Σvalues. DMNA dislays the lowest energy content among the substances studied[7]which is connected with its negative oxygen balance.Its negativeVS,Σvalue might be a result of the predominant influence of the strong negative inductive (mesomeric) effect of the nitro group over the weak positive inductive effects of the two methyl groups, see a demonstration in Scheme 2.

Scheme 2 Inductive effects in the 2-nitro-2-azapropane molecule (DMNA)

TheEaandVS,Σvalues of the nitramines studied were obtained by comparison of the activation energies of thermal decomposition and have been correlated in Fig.3. Allocating nitramines into sub-groups according to this Figure recalls very much their allocation in the sense of the relationship between theEavalues and the square of detonation velocity[47]and, to some extent, also the relationship between theseEavalues and15N NMR chemical shifts of the nitrogen atoms in the primary reactive nitro groups[9, 12, 15]in the nitramino groupings; it is clear that these shifts have a direct connection to the electronic configuration in the reaction center of the given molecules (see in Refs. 9, 12 and 15) which is valid also for theVS(r) values.

a. BCHMXb. HMXc. DINGU

d. TEXe. HNIW

Fig.1 TGA results from heating under isothermal TG at 190 ℃ for 30 min

a. originalβ-HMX crystals (white color)b. heatedβ-HMX crystals with cracks(dark white color) c. original BCHMX crystals (white color)

d. heated BCHMX crystals with bubble traces(white color)e. originalε-HNIW crystals (white color)f. heatedε-HNIW crystals with surface cracks(yellow color)

Fig.2 A comparison of surface structure for an original crystal ofβ-HMX, BCHMX andε-HNIW with that of the one heated under isothermal TG at 190 ℃ for 30 min using the SEM technique

The nitramines associated with line Ⅰ decompose in their solid state. Group Ⅱ corresponds to those which decompose in the liquid state and data 16.3 and 16.4 forε-HNIW correlate well with this line (they have been published for solid state decomposition[40-41]) and are also in good correlation with group Ⅰ. In another group, around line Ⅱ, nitramine HMX (data 10.3) might melt in its decomposition products[9]: decomposition of solid compounds proceeds very often through the liquid phase, formed as a result of the melting of impurities, the decomposition products, or their eutectic mixture with the original substance[13, 16].This is the problem of the different specifications in the kinetics of the HMX decomposition in its supposed liquid and solid states[9, 12]. This might also be the case with BCHMX and especially with HNIW.

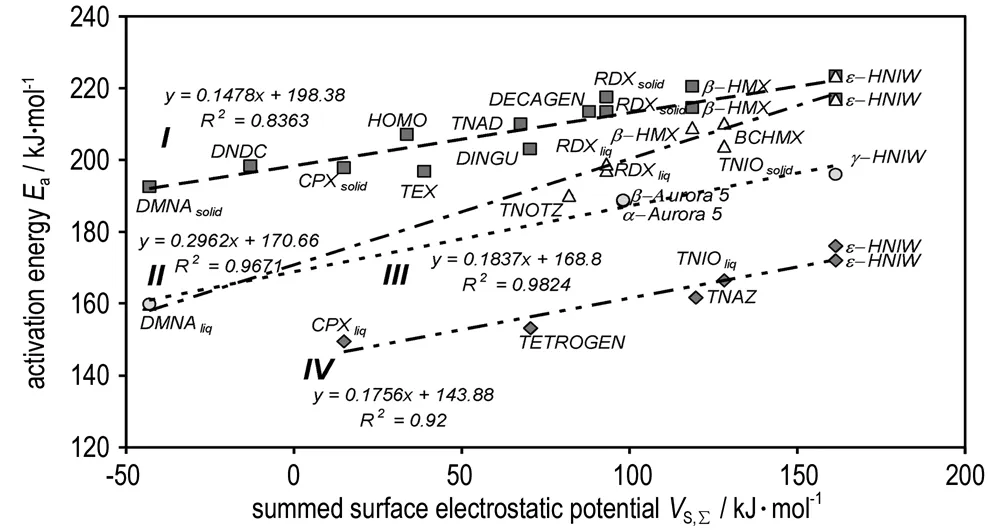
Fig.3 Relationship between the activation energies of thermal decomposition and theVS,Σvalues

One difference between theβ-HMX and BCHMX molecules lies in the presence of crowding in the latter[48](it has a rigid structure). As Fig.3 show, theβ-HMX crystal forms cracks when heated for 30 minutes at 190 ℃ due to theβδtransition; the process of the decomposition of HMX during this polymorphous transition is proved only by rather high starting gas-evolution[49]-see the corresponding TG record in Fig.1. On the other hand, melting-dissolution of the BCHMX crystals (Fig.2(c) and (d)) leads to relatively quick and more profound decomposition at 190 ℃ (TG record in Fig.1). A visual melting point of BCHMX is at 262 ℃ with decomposition[48]and, using DTA measurements, no endothermic or exothermic reaction is detected before 205 ℃[47-48]. It is possible to find similar behavior for the TNIO crystals (this nitramine is structurally similar to BCHMX). Nedelko et al.[42]have studied thermal decomposition of various modifications of HNIW and shown that all modifications before such decomposition are transferred intoγ-HNIW. This transfer follows a complicated process[42]and the positions of the ε-HNIW data No. 16.4 (group Ⅰ) and the already mentioned No. 16.3 (group Ⅱ) might be connected with this fact. This fully corresponds with the same findings in paper[47].

Similarly, as in paper[47], line Ⅲ in Fig.3 corresponds to decomposition probably in the transit liquid-solid state; here the data forγ-HNIW (i.e. No.16.5) correlate well. Chukanov et al. stated[50]that the polymorphic transition changes the conformation on the HNIW molecule, the stressed aza atom appears and the co-linear nitrogen lone electron pairs are thus differently oriented here. This change is preceded by an induction period with the formation of active microregions which are loaded by a mechanical stress gradient[50]. Damage to the resultant crystal ofγ-HNIW by this way might be as shown in Fig.2f. We did not have the possibility to study the Aurora′s crystals. It is clear that the polymorphic transition should be influenced by the state of perfection and purity of the originalε-HNIW crystal. HNIW also decomposes more rapidly under evacuation than in air or argon, i.e. the dynamic vacuum provides sublimation (in comparison-HMX sublimes more rapidly than has time of decompose)[41]. The positioning of the HNIW data in Fig.3 may be connected with these statements.

The positioning of the DMNA data, i.e.data for a non-cyclic nitramine, in Fig.3 is logical, and all compounds belonging to the lines Ⅰ, Ⅱ and Ⅲ, can be derived by hypothetical substitutions from this nitramine. DMNA being associated with cyclic nitramines has already been shown in the framework of the physical stability study of nitramines[43].

Line Ⅳ in Fig.3 groups those nitramines with crowded molecules, mostly in the liquid state. Inclusion of data 16.1 and 16.2 for HNIW with this group might be mainly due to crowding in its molecule but also by the above-mentioned dissolution of its crystal in impurities and products of the HNIW decomposition; in each case, data 16.1 and 16.2 correspond to the HNIW thermal decomposition in its liquid state(solution).

Reduction of the rate of the mono-molecular reactions and, accordingly, an increase in the stability of the substance when moving from a liquid condition to a solid state is determined by the heat of fusion of the substance, ΔHm,tr, and by the linear sizes of crystal grain[16]. The relationship between this stabilization force and theVS,Σvalues in the nitramines studied is not without interest; Fig.4 represents a comparison of these ΔHm,trandVS,Σvalues. Here all relationships have a strictly molecular-structural nature. While the lines in this Figure with a positive slope correspond to the prevailing influence of the molecule size, the line with a negative slope is associated with the prevailing influence of orientation interactions in the molecular crystal; this last can be shown by the trend in the melting points peaks (determined by DSC[43]). These are: for DNDC 490 K, for RDX 477.5 K, forβ-HMX predicted at 465.2 K and for BCHMX there has already been an indication of melting-dissolution observed at about 463 K (i.e. 190 ℃, Fig.2d). Both the last mentioned nitramines do not have genuine experimental melting points (for HMX see discussion in papers[9, 51]). Using this relationship (i.e. with the negative slope) the ΔHm,trvalues for TNOTZ and TNIO might be predicted (32.67 and 32.07 kJ·mol-1, respectively) because they are both structurally similar to the group of compounds concerned. It is also clear that allocating the nitramines studied into sub-groups according to Fig. 3 and following Fig.5 is connected with the actual intermolecular interaction in the nitro compounds studied at the time of their thermal decomposition.

As presented in paper [47], the rate constantskfor 230 ℃ were calculated from Arrhenius parameters of the nitramines studied here (see in Table 1). In the paper mentioned[47], a semi-logarithmic relationship was derived between thek230 ℃values and detonation velocities of these nitro compounds. As Fig. 5 shows, a similar relationship exists also between thek230 ℃andVS,Σvalues. By comparing Fig.3 and Fig.5, it seems that intermolecular interactions have a slightly different influence on thekvalues than on theEavalues, judging from the data belonging to the corresponding lines. Thus, groupAcorresponds predominantly to decomposition in a solid state with data for liquid DMNA also correlating well. This group includes also the BCHMX data which “hover” between decomposition in solid and liquid states (see paper [47] and Fig.3). GroupB, for the most part, corresponds to groupⅡ in Fig.3. GroupCrepresents decomposition of the nitramines in the liquid state; it corresponds to groups Ⅱ and Ⅲ in Fig.3. LineEin Fig.5 represents increasing reactivity with increase of oxygen balance and decrease of peak melting point temperature in the order DNDC-TETROGEN-TNAZ (490 K[43]-436.1 K[43]-373 K[27]). A similar situation might be shown in the case of lineF, especially in the order of RDX-HMX-TNIO-HNIW (but the exact melting point of HNIW has not yet been examined); a certain exception from this group are the data for the solid state decomposition of DMNA-all the nitramines mentioned in this group can be hypothetically derived from this simple nitramine[43].

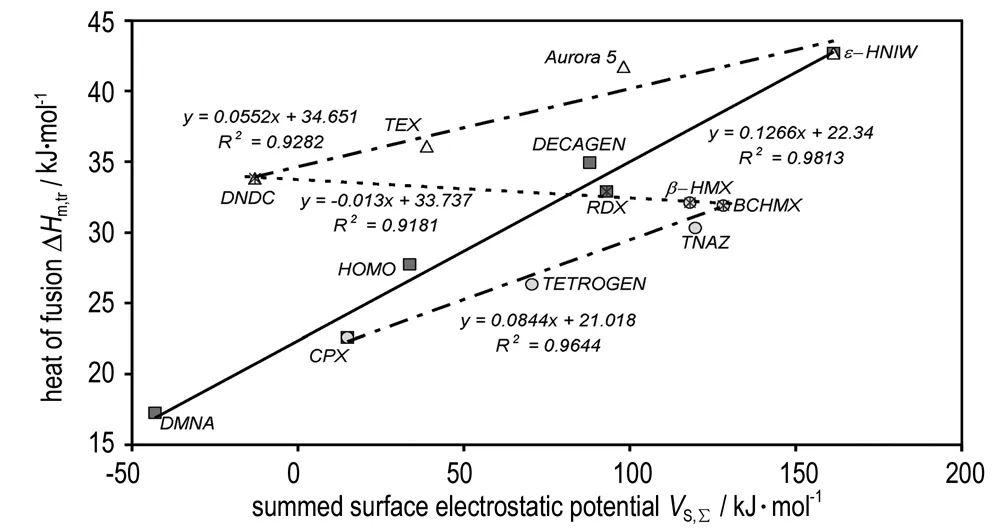
Fig.4 Relationship between the heat of fusionHm,trand theVS,Σvalues.

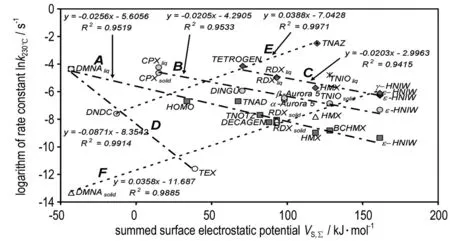
Fig.5 Relationship between the logarithms of the rate constantskat 230 ℃ and theVS,Σvalues

4 Conclusions

Taking the sum of the maximum positive,VS,maxand minimum negative,VS,minvalues of molecular surface electrostatic potentials (ESPs) as a criterion of the imbalance between these extremes, a new simple characteristic of ESPs results, namely the summed molecular surface electrostatic potentialVS,Σ. TheseVS,Σvalues have close relationships to the characteristics of the nitramines′ reactivity, in this case to their low-temperature thermal decomposition. Specifically, correlating theVS,Σvalues with the activation energies,Ea, of this process allows drawing conclusions about the physico-chemical behavior of these nitramines during their thermal decomposition, because the summed ESPs have a direct logical relationship to the heats of fusion of these nitro compounds. Similarly it is possible to say the same about the semi-logarithmic correlation of the uni-molecular rate constant for the given temperature (kt) with theVS,Σvalues. These possibilities can be demonstrated with the decomposition ofcis-1,3,4,6-tetranitrooctahydroimidazo-[4,5-d]imidazole (BCHMX) in its alleged solid state (sintering of the crystal surfaces), of 1,3,5,7-tetranitro-1,3,5,7-tetrazocane (HMX-cracking of its crystals duringβδtransition) and especially of 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane (HNIW). The results documented in this paper confirm the problems encountered in the kinetic specification of the thermal decomposition of HMX and especially HNIW[47]which, in the case of HNIW, can be connected also with complications in its polymorph transitions[42, 47]and its level of purity. The facts discovered here suggest a need to study the pre-decomposition states on thermal decomposition and beginning phase of initiation of the nitramines′ molecule′s crystals.

Acknowledgements

[1] Politzer P, Murray J, Sensitivity Correlation[M]∥Politzer P, Murray J. Theoretical and Computational Chemistry, Vol. 13, Energetic Materials, Part 2, Detonation, Combustion. Amsterdam: Elsevier B V , 2003: 5-23.

[2] Rice B M. Applications of Theoretical Chemistry in Assessing Energetic Materials for Performance or Sensitivity, in: Shaw RW, Brill TB, Thompson DL. Overviews of Recent Research on Energetic Materials. Advanced series in Physical Chemistry[M]. Singapore: World Sci Publ Co Ptc Ltd, 2005,16: 335-367.

[3] Rice BM, Byrd EFC, Mattson WD, Computational Aspects of Nitrogen-Rich HEDMs[M]∥ Klapoetke T.HighEnergyDensityMaterials,Series:Structure&Bonding, 125.New York: Springer, 2007: 153-194.

[4] Sorescu D C, Rice BM, Theoretical predictions of energetic molecular crystals at ambient and hydrostatic compression conditions using dispersion corrections to conventional density functionals (DFT-D)[J].JPhysChem, 2010, C 114: 6734-6748.

[5] Pospisil M, Vavra P, Concha M. C, et al. A possible crystal volume factor in the impact sensitivities of some energetic compounds[J] .JMolModel, 2010, 16(5): 895-901.

[6] Licht H-H, Performance and Sensitivity of Explosives[J].Propellants,Explos,Pyrotech, 2000, 25: 126-132.

[7] Zeman S, Friedl Z, A New Approach to the Application of Molecular Surface Electrostatic Potential in the Study of Detonation[J].Propellants,Explos.Pyrotech, 2012, 37(5): 609-613.

[8] Zeman S. Modified Evans-Polanyi-Semenov relationship in the study of chemical micromechanism governing detonation initiation of individual energetic materials [J].ThermochimActa, 2002, 384: 137-154.

[9] Zeman S, Analysis and Prediction of the Arrhenius Parameters of Low-Temperature Thermolysis of Nitramines by means of the15N NMR Spectroscopy[J].ThermochimActa, 1999, 333: 121-129.

[10] Zeman S, Kinetics Compensation Effect and Thermolysis Mechanisms of Organic Polynitroso and Polynitro Compounds[J].ThermochimActa, 1997, 290: 199-217.

[11] Andreev KK, Belyaev AF. Teoriya vzryvchatykh veschestv (Theory of Explosives)[M]. Oborongiz, Moscow, 1960. Transl as U S Govt Rep AD-643597, NTIS, Springfield, 1966.

[12] Zeman S. A Study of Chemical Micro-Mechanisms of Initiation of Organic Polynitro Compounds[M]∥ Klapoetke T (Ed), High Energy Density Materials, Series: Structure & Bonding, Vol. 125, Springer, New York, 2007: 195-271.

[13] Manelis G B, Nazin G M, Rubtsov Yu I, et al. Thermal Decomposition and Combustion of Explosives and Propellants[M]. Taylor & Francis, New York, 2003.

[14] Shackelford S A.Role of thermochemical decomposition in energetic material initiation sensitivity and explosive performance[J].CentrEurJEnergetMater, 2008, 5(1): 75-101.

[15] Zeman S. A Study of Chemical Micro-Mechanisms of Initiation of Organic Polynitro Compounds[M]∥Politzer P, Murray J (Eds.), Theoretical and Computational Chemistry, Vol. 13, Energetic Materials, Part 2, Detonation, Combustion(Eds: Politzer P, Murray J) . Amsterdam: Elsevier B V , 2003: 25-52.

[16] Manelis G B, Nazin G M, Prokudin, V G. Prognosis of energetic compounds stability in solid phase [J].CentrEurJEnergetMater, 2009, 6(1): 31-44.

[17] Gol′binder A I. Laboratornye raboty po kursu teorii vzryvchatykh veschestv (Laboratory Practice in the Theory of Explosives)[M]. Rosvuzizdat, Moscow, 1963: 9 (in Russian).

[18] Andreev K K. Termicheskoe razlozheniye i goreniye vzryvchatykh veschestv(Thermal Decomposition and Combustion of Explosives)[M]. Izdat Nauka, Moscow, 1966 (in Russian).

[19] Chukanov N V, Korsoonskii B L, Dubovitskii F I, et al. IR-Spectroscopic Determination of Monomolecular Dissociation Activation Energies.N-Nitrodimethylamine [J].DoklAkadNaukSSSR, 1983, 265: 1445-1447(in Russian).

[20] Sitonina G V, Korsoonskii B L, Pyatakov N F, et al. Kinetics of the thermal decomposition of n,n′-dinitropiperazine and 1,3-dinitro-1,3-diazacyclopentane[J].IzvAkadNaukSSSR,SerKhim, 1979, 311-314(in Russian).

[21] Robertson A J B. Thermal decomposition of explosives. II. cyclotrimethylenetrinitramine (cyclonite) and cyclotetramethylenetetranitramine [J].TransFaradaySoc, 1949, 45: 85-93.

[22] Zeman S, Relationship between the arrhenius parameters of the low-temperature thermolysis and the13C and15N chemical shifts of nitramines[J].ThermochimActa, 1992, 202: 191-200.

[23]Spartan′10 Win-P, Wavefunction[M]. CA: Inc Irvine , 2010.

[24] Bondi A. Physical Properties of Molecular Crystals, Liquids, and Glasses[M]. New York: John Wiley & Sons, 1968.

[25] Pavlov A N, Fedotov A A, Pavlova L L, et al. Novozhilov B V, Chemical Physics of the Processes of Combustion and Explosion[C]∥Proc. 9th All Union Symp. Compust. Explos, Acad Sci USSR, Chenogolovka, 1989: 103. (in Russian).

[26] Grice, M E, Habibollahzadeh D, Politzer P. Calculated structure, heat of formation and decomposition energetics of 1,3-dinitro-1,3-diazacyclobutane[J].JChemPhys, 1994, 100: 4706-4707.

[28] Sitonina G V, Korsoonskii B L, Pyatakov N F, et al. Kinetics of Thermal Decomposition of N,N′-Dinitropiperazine and 1,3-Dinitro-1,3-diazacyclopentane[J].IzvAkadNaukSSSR,SerKhim, 1979, 311-317 (in Russian).

[29] Stepanov R S, Kruglyakova L A, Astakhov A M. Thermal decomposition of some quinary cyclic nitramines[J].ZhObshKhim, 2006, 76: 2061-2062.

[30] Janney J L, Rogers R N.Thermochemistry of Mixed Explosives[C]∥Proc. 7thInt Conf Thermal Anal, Part 2. Kingston, Canada, August 1982:1426; US Govt. Report D E 820 12 149, 1982.

[31] Maksimov Yu Ya.Termicheskoe razlozheniye geksogena i oktogena (Thermal Decomposition of Hexogen and Octogen)[J].TrMoskKhim-TekhnolInstimMendeleeva, 1967, 53: 73-84.

[32] Stepanov R S, Kruglyakova L A, Astakhov A M. Thermal decomposition of some cyclic nitramines[J].ZhObshKhim, 2006, 6: 525-526.

[33] Stepanov R S, Kruglyakova L A, Astakhov A M. Kinetics of thermal decomposition of some nitramines with two condensed quinary cycles[J].ZhObshKhim, 2006, 76: 2063-2063.

[34] Rogers R N.Differential scanning calorimetric determination of kinetics constants of systems that melt with decomposition[J].ThermochimActa, 1972, 3: 437-447.

[35] Results of Goshgarian B B. -cited in paper by Brill T B, Karpowicz R J, Solid Phase Transition Kinetics. The Role of Intermolecular Forces in the Condensed-phase Decomposition of Octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine[J].JPhysChem,1982, 86: 4260-4265.

[36] Hu R, Yang Z, Liang Y.The Determination of the most probable mechanism function and three kinetic parameters of exothermic decomposition reaction of energetic materials by a single non-isothermal DSC curve[J].ThermochimActa, 1988, 123: 135-151.

[37] Stepanov R S, Rogozin M V, Kruglyakova L A, et al. Kinetics regularity of thermal decomposition of 4,10-dinitro-2,6,8,12-tetraoxa-4,10-diazatetracyclo[5.5.0.0.5,9)3,1,1] dodecane[J].Kinet.Katal, 1999, 40: 58-60.

[38] Lübbecke S, Bohn M A, Pfeil A, et al. Thermal behavior and stability of HNIW (CL-20)[C]∥Proc. 29thInt. Annual Conf. ICT, Karlsruhe, 1998: 145/1.

[39] Östmark H, Bergman H. Proc. Int Symp Energet Materials Technol [C]∥Am Def Prep Assoc, Meeting680, Phoenix, Arizona, 1995: 76.

[40] Stepanov R S, Kruglyakova L A.Structure-kinetics relationships of thermodestruction of some framework nitramines[J].RussJGenChem, 2010, 80: 316-322.

[41] Korsounskii B L, Nedelko V V, Chukanov N V, et al. Kinetics of thermal decomposition of hexanitrohexaazaisowurtzitane[J].RussChemBull, 2000, 49(5): 812-818.

[42] Nedelko V V, Chukanov N V, Raevskii A V, et al. Comparative investigation of thermal decomposition of various modifications of hexanitrohexaazaisowurtzitane (CL-20)[J].Propellants,Explosives,Pyrotechnics, 2000, 25: 255-259.

[43] Zeman S. Some Predictions in the field of the physical thermal stability of nitramines[J].ThermochimActa,1997, 302: 11-16.

[45] Atalar T, Zeman S. A new view of relationships of the N-N bond dissociation energies of cyclic nitramines. part i. relationships with heats of fusion[J].JEnergMater, 2009, 27(3): 186-199.

[46] Zeman S, Jalovy Z. Heats of fusion of polynitro derivatives of polyazawurtzitanes[J].ThermochimActa, 2000, 345: 31-38.

[49] Burov Yu, Dubikhin V, Kovalchukova O.Features of kinetics of thermal destruction of HMX[C]∥Proc. 11thSeminar “New Trends in Research of Energetic Materials,Univ of Pardubice, 2008: 476-479.

[50] Chukanov N V, Dubovitskii V A, Zakharov V V, et al. Phase transformations of 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane: the role played by water, dislocations and density[J].RussJPhysChemB, 2009, 3(3): 486-493.

[51] Brill T B, Karpowicz R J, Solid Phase Transition Kinetics. The Role of Intermolecular Forces in the Condensed-phase Decomposition of Octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine[J].JPhysChem, 1982, 86: 4260-4265.